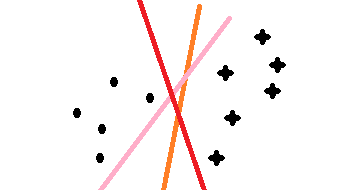
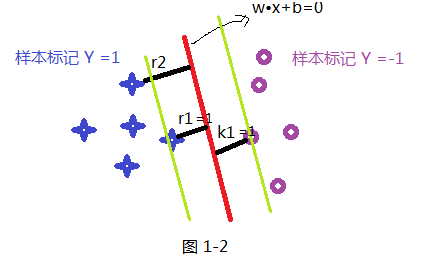
svm算法的通常理解在二维问题上,对于二元分类来说,svm的目的就是找一条线把两类分开。不过下面这个例子,有三条不同的直线都能把这两类分开,那么我们该选哪一条线呢?这将是我们考虑的问题:
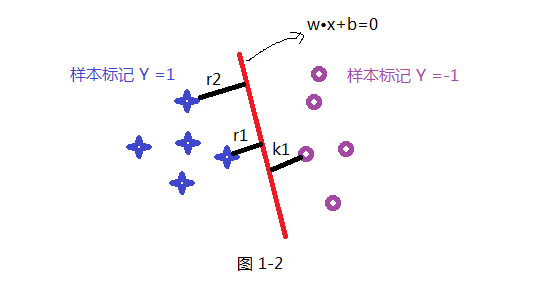
首先我们先假设一条直线W*X+b=0是最优的分割线。我们把这种最优SVM分割平面叫做超平面,我们现在的目标就是确定最优的W和b的值。SVM定义超平面为:能使支持向量和超平面之间的最小距离的最大值。那么这句话该如何理解?我们结合着下面这张图:让支持向量和超平面之间的最小值最大化,目的就是使两个类到超平面的间隔是最大的,我们不考虑所有的点和超平面之间的关系,只考虑和超平面最近的点。分类按照这个标准不难理解,因此也就不难理解为什么要求超平面。
根据上面的假设,我们提出已知条件:有蓝色星星样本5个,假设它们代表的类Y=1;同时有紫色圆圈样本5个,假设它们代表的样本Y=-1;因此T={(x1,y1),(x2,y2),(x3,y3)......},超平面方程为W*x+b=0。样本点到超平面的几何距离为:
这个距离大家可以推导一下,按照点到直线距离推导即可,这里就不推理验证了。
下面的问题就是怎样获取超平面:
超平面定义为:支持向量到超平面的最小距离的最大值,即:max[支持向量到超平面的最小距离]。可以表示如下:
加入约束:min yi(w*xi+b) = 1,因此:其他的样本点的函数距离一定是大于1。即y(w*x+b) >= 1,把这个条件带到公式进行优化,得到公式1-3:
在公式1-3的基础上再进行优化,优化最大化分数,转化为优化最大化分母,将公式转化为1-4
为了优化1-4,利用拉格朗日公式和KTT条件,转化如下:
其中列出相等的两个部分是等价的,因此最终我们可以写成对偶表达式的形式:
因此要先求最小值,对w,b求偏导:
把上面求得的参数带入公式优化max:
最终得到超平面。








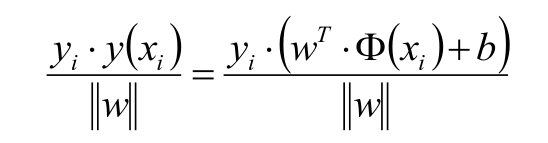
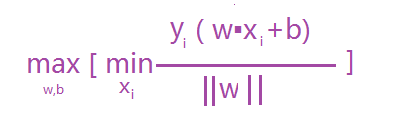
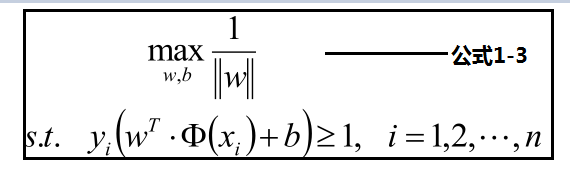
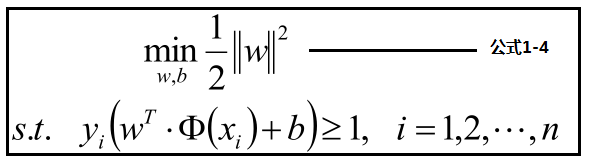
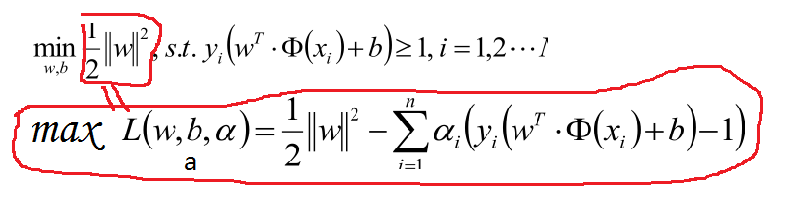


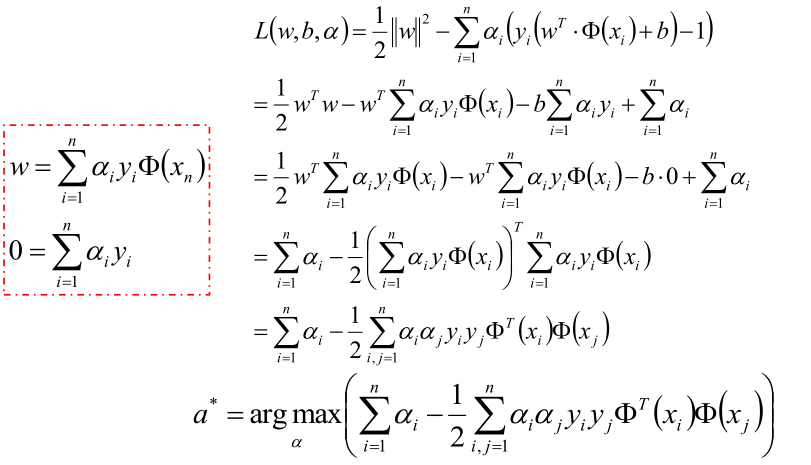















 5492
5492











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








