神经网络-1——摘录《机器学习算法导论》第八章

jeanette77

于 2022-11-18 16:16:41 发布

阅读量218

点赞数

分类专栏：机器学习算法导论文章标签：神经网络算法

本文链接：https://blog.csdn.net/comeon77/article/details/127056519

版权

机器学习算法导论专栏收录该内容

2 篇文章 0 订阅

订阅专栏

第八章神经网络

近年来，计算机芯片的高速发展大幅提升了计算机的计算能力，这使得训练大型的神经网络模型成为可能，由此基于神经网络的深度学习技术展示出其前所未有的威力，神经网络重新回到了人们的视野中心。

8.1 神经网络基本概念

8.1.1 神经网络模型

神经网络是模拟人类神经结构的机器学习学习算法。人类的神经呈层状网络分布，由众多脑神经元构成。每个神经元包含三部分：树突--负责接收其他神经元传来的信号、胞体--对所有树突传来的信号进行处理并生成一个输出信号、轴突--将胞体生成的输出信号传送至与其相连的所有其他神经元的树突。人脑的工作原理是通过神经元组成的层状网络结构，将接收到的外界信息经过层层加工后做出反应。

神经网络算法是对上述原理的模拟和抽象，有三要素：1.n个权重 $\omega _{1}, \omega _{2},...\omega _{n} \in \mathbb{R}$ ； 2.偏置值 $b\in \mathbb{R}$ ; 3.激活函数 $\sigma :\mathbb{R}\rightarrow \mathbb{R}$ 。假设神经元接到n个输入 $x_{1},x_{2},...,x_{n}$ ，每条树突上对应一个权重，信息通过树突传入胞体，胞体首先计算他们加权和,随后将激活函数作用在加权和上，最后将 $\sigma \left (\sum_{i}^{n} \omega _{i}x_{i}+b\right )$ 作为神经元的输出由轴突传出。

计算加权和是胞体对信息的综合，随后激活函数是对信息进行处理和转化。激活函数是对人脑神经元功能的模拟。常用激活函数有Identity激活函数、ReLu激活函数、Sigmoid激活函数、Tanh激活函数。

Identity激活函数对信息不做任何变换而直接输出，其功能是如实传递信息。

$identity\left ( x \right )=x$

ReLu激活函数全称 Rectified Linear Unit （线性修正单元），只激活取值为正的信息，用于模拟人脑过滤无用信息。

$relu\left ( x \right )=max\left \{ 0,x \right \}$

Sigmoid激活函数取值在[0,1]之间，其功能是随着信息强度的增强而平滑地激活信息。

$sigmoid\left ( x \right )=\frac{1}{1+e^{-x}}$

Tanh激活函数与Sigmoid激活函数类似，但其取值区间在[-1,1]之间，相对于原点对称，有时能简化运算。

$tanh\left ( x \right )=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

神经元计算单元之间可以传输信息，即一个神经元的输出可以作为其他神经元的输入，这样，一组神经元计算单元组合在一起完成信息的处理和传递任务。

神经网络的每一层都由神经元组成，且每层神经元个数可以不同，但每一层中的神经元都与其上一层中的每个神经元相连。一般地，将第i层的神经元输出作为第i +1层神经元的的输入，层层传递，直至最后一层。其中神经网络的最后一层被称为输出层，其他的为隐藏层。

上述描述可知，同层神经元都有相同数量的输入。通常假设同层神经元具有相同的激活函数，因此整个网络每层还有两组参数值需要确定：权重矩阵和偏置向量。在n个输入和R层神经网络中，设第r层含有 $m_{r}$ 个神经元（r=1,2...R）,记 $m_{0}=n$ 。

一个 $m_{r}$ * $m_{r-1}$ 权重矩阵 $W^{\left ( r \right )}$ 。 $W^{\left ( r \right )}$ 中元素 $\omega _{ij}^{\left ( r \right )}$ 表示第r层的第i个神经元与第r-1层的第j个输出之间边所带的权重。（i=1,2,... $m_{r}$ ; j=1,2,... $m_{r-1}$ ）
一个 $m_{r}$ 维的偏置向量 $b^{\left ( r \right )}$ 。其分量 $b_{i}^{\left ( r \right )}$ 表示第r层的第i个神经元的偏置值（i=1,2,... $m_{r}$ ）
用 $v^{\left ( r-1 \right )}$ 表示第r-1层所有神经元输出构成的列向量，设 $\sigma ^{\left ( r \right )}$ 表示第r层的激活函数，那么第r层的第i个神经元的输出为
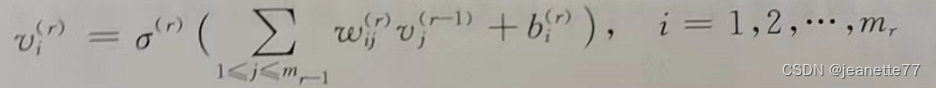
为简化记号，定义 $s^{\left ( r \right )}=W^{\left ( r \right )}v^{\left ( r-1 \right )}+b^{\left ( r \right )}$ ,则第r层中所有的神经元的输出可表示为 $v^{\left ( r \right )}=\sigma ^{\left ( r \right )}\left ( s^{\left ( r \right )} \right )$

综上所述，神经网络模型可描述为：给定一个R层的神经网络，设第r层的权重矩阵、偏置向量和激活函数分别为 $W^{\left ( r \right )}$ 、 $b^{\left ( r \right )}$ 、 $\sigma ^{\left ( r \right )}$ （r=1,2...R）。下面的伪代码描述了神经网络对任意输入向量x 计算输出 $v^{\left ( R \right )}$ 的模型。

v_0=list[input(x)]
for r=1,2...R
    s_r=w_r*v_(r-1)+b_r
    v_r=f_r(s_r)
return v_R

8.1.2 神经网络算法描述

神经网络算法是模型假设为神经网络模型的经验损失最小化。它既可以应用于分类问题，也可以应用于回归问题。

一个神经网络模型分为两部分：网络结构与模型参数。网络结构包括层数、每层神经元的个数、每层激活函数。参数模型包括每层的权重矩阵和偏置向量。对于给定的网络结构，不同的模型参数对应的神经网络模型是不同的。

一般地，网络结构有算法设计者事前设定好，由神经网络算法计算基于设计好的网络结构的最优模型参数。

以回归问题为例，n个输入、1个输出的网络结构。神经网络算法的任务是训练模型参数来使得损失函数——均方误差最小化。

神经网络回归算法

样本空间 $X\subseteq \mathbb{R}^{n}$

输入：m条训练数据， $S=\left \{ \left ( x^{1},y^{1} \right ) ,\left ( x^{2},y^{2} \right ),...\left ( x^{m},y^{m} \right )\right \}$

模型假设H：一个含有n个输入、1个输出的网络结构

任务：找到最优模型h

$\arg min \frac{1}{m}\left ( h\left ( x^{\left ( i \right )} \right ) -\left ( y^{\left ( i \right )} \right ) \right )^{2}$

以分类问题为例，n个输入、k个输出在加上softmax变化的网络结构。神经网络算法的任务是训练模型参数来使得目标函数——k元交叉熵最小化。

神经网络分类算法

输入：m条训练数据 $S=\left \{ \left ( x^{1},y^{1} \right ) ,\left ( x^{2},y^{2} \right ),...\left ( x^{m},y^{m} \right )\right \}$

特征组x=( $x_{1},x_{2},...,x_{n}$ ) ,输出为v= $\left ( v_{1} ,v_{2} ,...v_{k} \right )$

$softmax\left ( v_{i} \right )=\frac{e^{v_{\left ( i \right )}}}{\sum_{j}^{}e^{v_{\left ( j\right )}}}$

模型输出为： $h \left ( x \right )=\left ( softmax\left ( v_{1} \right ),softmax\left ( v_{2} \right ),...softmax\left ( v_{k} \right ) \right )$

任务：找到最优模型h

$\arg min -\frac{1}{m}\sum_{i=1}^{m}\left \langle y^{\left ( i \right )} ,\log h\left (x^{\left ( i \right )} \right )\right \rangle$

8.2 神经网络优化算法

由于神经网络算法的目标函数往往不是关于模型参数的凸函数，所以随机梯度下降算法可能收敛到局部最优解，不一定是全局最优。然而实际应用中，神经网络的局部最优可以近似全局最优，因此随机梯度下降算法仍然是十分实用的神经网络优化算法。（具体随机梯度下降算法见第四章）

根据神经网络模型可知，第r层的输出是第r-1层的输出、第r层的权重矩阵和偏置向量的函数，而第r-1层的输出又是第r-2层的输出、第r-1层的权重矩阵和偏置向量的函数，以此类推可知，最后的输出是所有层权重矩阵和偏置向量以及最初输出的函数。相应地，模型对应的损失函数也是所有层权重矩阵和偏置向量以及最初输出的函数。

随机梯度下降算法是在每一轮循环中对随机选取的训练数据计算其损失函数的梯度，并沿着梯度的反方向调整模型的参数取值。

神经网络的随机梯度下降算法

for each r i j:

$\omega _{ij}^{\left ( r \right )}$ = random number

$b_{i}^{\left ( r \right )}$ =0

for t=1,2...N:

Sample (x,y) ~S

$v^{\left ( R \right )}=h_{W,b}\left ( x \right )$

$\left ( \frac{\partial L}{\partial \omega _{ ij}^{\left ( r \right )}} ,\frac{\partial L}{\partial b _{ i}^{\left ( r \right )}}\right )=BackProp\left ( v^{\left ( R \right )} ,y\right )$

for each r,i,j：

$\omega _{ij}^{\left ( r \right )}\leftarrow \omega _{ij}^{\left ( r \right )}-\eta \frac{\partial L}{\partial \omega _{ij}^{\left ( r \right )}}$

$b_{i}^{\left ( r \right )}\leftarrow b_{i}^{\left ( r \right )}-\eta \frac{\partial L}{\partial b_{i}^{\left ( r \right )}}$

return $h_{W,b}$

随机梯度算法有两个算法参数：循环的轮数N 和学习速率 $\eta$ 。

在每轮循环中，算法随机选取一条训练数据（x,y），随后：（1）计算当前参数对应的神经网络模型 $h_{W,b}$ 在x上的输出 $v^{\left ( R \right )}$ ；（2）调用反向传播算法BackProp ，根据 $v^{\left ( R \right )}$ 和y来计算L对各个参数的梯度；（3）获得各梯度值后，算法沿每个参数的梯度反方向以 $\eta$ 为步长更新参数值（学习速率 $\eta$ 为随机梯度算法参数之一）。（4）在指定搜索步数进行N轮循环后，随机梯度下降算法返回最终的模型（循环的轮数N为随机梯度算法另一参数）。

什么是反向传播算法BackProp？为什么在梯度计算时要用反向传播算法BackProp？

书上推导十分详细，这里暂不展开，可能以后单独会写。

直接上反向传播算法得到的结论：

第一步，求解损失函数对输出的偏导值。

$\delta ^{\left ( R \right )}=\frac{\partial L}{\partial v^{\left ( R \right )}}$