【题解】[Swerc2008]First Knight

sol：
如果你把满足上述条件的所有等式画成一个矩阵，你会发现 所有非零元素（除了最后一列常数项）位于距离对角线 ±d 的范围内。对这样的矩阵进行高斯消元，称作带状矩阵的高斯消元。

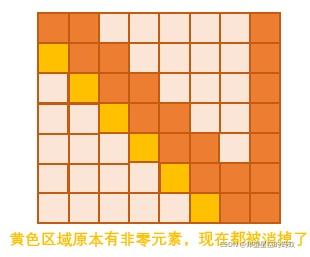
如上图，带宽为 2 ，那么每次就是一个 2 * 2 矩阵的高斯消元。

上述消元过程是 $o(n{d}^2)$ 的 ： o(n) 枚举 i 行，对于用每一行给下方 d 行消元，每一行的消元只会枚举不超过 d 个未知数。

从本题上看，就是一个为 2n+1 ，宽为 2m+1 的带宽矩阵。

当然这种做法并没有考虑到有非常多的 0，如果进一步压缩（只遍历初始不为 0 的位置）会更快。

本题时间复杂度 $o((nm{)}^2)$ 。

#include <bits/stdc++.h>
#define db double
#define eps 1e-18
using namespace std;
const int N = 45 * 45;
int n, m;
int dx[4] = { 1, 0, -1, 0 }, dy[4] = { 0, 1, 0, -1 };
db p[4][N][N], A[N][N], ans[N];
int has(int i, int j) { return (i - 1) * m + j; }
void gauss() {
    int r, c;
    for (r = 1, c = 1; r < n * m && c <= n * m; r++, c++) {
        int p = r;
        for (int i = r; i < n * m; i++) {
            if (fabs(A[i][c]) > fabs(A[p][c]))
                p = i;
        }
        //思考一下带宽矩阵消元的适合需不需要交换这两行？
        swap(A[r], A[p]);
        for (int i = r + 1; i < n * m && i <= r + 2 * n; i++) {
            if (fabs(A[i][c]) > eps) {
                db tmp = A[i][c] / A[r][c];
                for (int j = c; j < n * m && j <= c + 2 * m; j++) {
                    A[i][j] -= A[r][j] * tmp;
                }
                A[i][n * m] -= A[r][n * m] * tmp;
            }
        }
    }
    for (int i = n * m - 1; i >= 0; i--) {
        for (int j = n * m - 1; j > i; j--) {
            if (fabs(A[i][j]) > eps) {
                A[i][n * m] -= A[i][j] * ans[j];
            }
        }
        ans[i] = A[i][n * m] / A[i][i];
    }
}
int main() {
    while (scanf("%d%d", &n, &m)) {
        for (int k = 0; k < 4; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= m; j++) {
                    scanf("%lf", &p[k][i][j]);
                }
            }
        }
        for (int i = 1; i < n * m; i++) {
            for (int j = 1; j <= n * m; j++) {
                A[i][j] = 0;
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (i == n && j == m)
                    continue;
                A[has(i, j)][has(i, j)] = 1;
                A[has(i, j)][n * m] = 1;
                for (int k = 0; k < 4; k++) {
                    int ti = i + dx[k], tj = j + dy[k];
                    if (ti < 1 || ti > n || tj < 1 || tj > m)
                        continue;
                    if (ti == n && tj == m)
                        continue;
                    A[has(i, j)][has(ti, tj)] = -p[k][i][j];
                }
            }
        }
        gauss();
        printf("%.10f\n", ans[1]);
    }
}