排序二叉树BST（binary search/sort tree）

之前介绍说，树这种存储结构，能提高数据的存储，读取效率。所以树的应用就可以体现在排序这一方面，比如有排序二叉树，平衡二叉树，红黑树等。本文介绍排序二叉树。

为啥有排序二叉树（二叉搜索树）的出现？这要从二分查找算法说起：

1.排序二叉树是一种特殊结构的二叉树，可以非常方便地对树中所有节点进行排序和检索。
2.排序二叉树要么是一棵空二叉树，要么是具有下列性质的二叉树：
3.若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
4.若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
5.它的左、右子树也分别为排序二叉树。
6.插入值与当前节点比较，如果相同，表示已经存在了，不能再插入。（即排序二叉树不能存在值相同的点）

排序二叉树：

BST树的搜索

BST树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左子节点；如果比结点关键字大，就进入右子节点；如果左子节点或右子节点的指针为空，则报告找不到相应的关键字；如果BST树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变BST树结构（比如插入与删除结点）无需移动大段的内存数据，甚至通常是常数开销。

如上图：右边也是一个BST树，但它的搜索性能已经是线性的了；同样的关键字集合有可能导致不同的树结构索引；所以，使用BST树还要考虑尽可能让BST树保持左图的结构，和避免右图的结构，也就是所谓的“平衡”问题；解决方案就是平衡二叉树了。

BST的创建

创建排序二叉树的步骤，也就是不断地向排序二叉树添加节点的过程，向排序二叉树添加节点的步骤如下：
以根节点当前节点开始搜索。
拿新节点的值和当前节点的值比较。
如果新节点的值更大，则以当前节点的右子节点作为新的当前节点；如果新节点的值更小，则以当前节点的左子节点作为新的当前节点。
重复 2、3 两个步骤，直到搜索到合适的叶子节点为止。
将新节点添加为第 4 步找到的叶子节点的子节点；如果新节点更大，则添加为右子节点；否则添加为左子节点。

BST删除节点

当程序从排序二叉树中删除一个节点之后，为了让它依然保持为排序二叉树，程序必须对该排序二叉树进行维护。维护可分为如下几种情况：

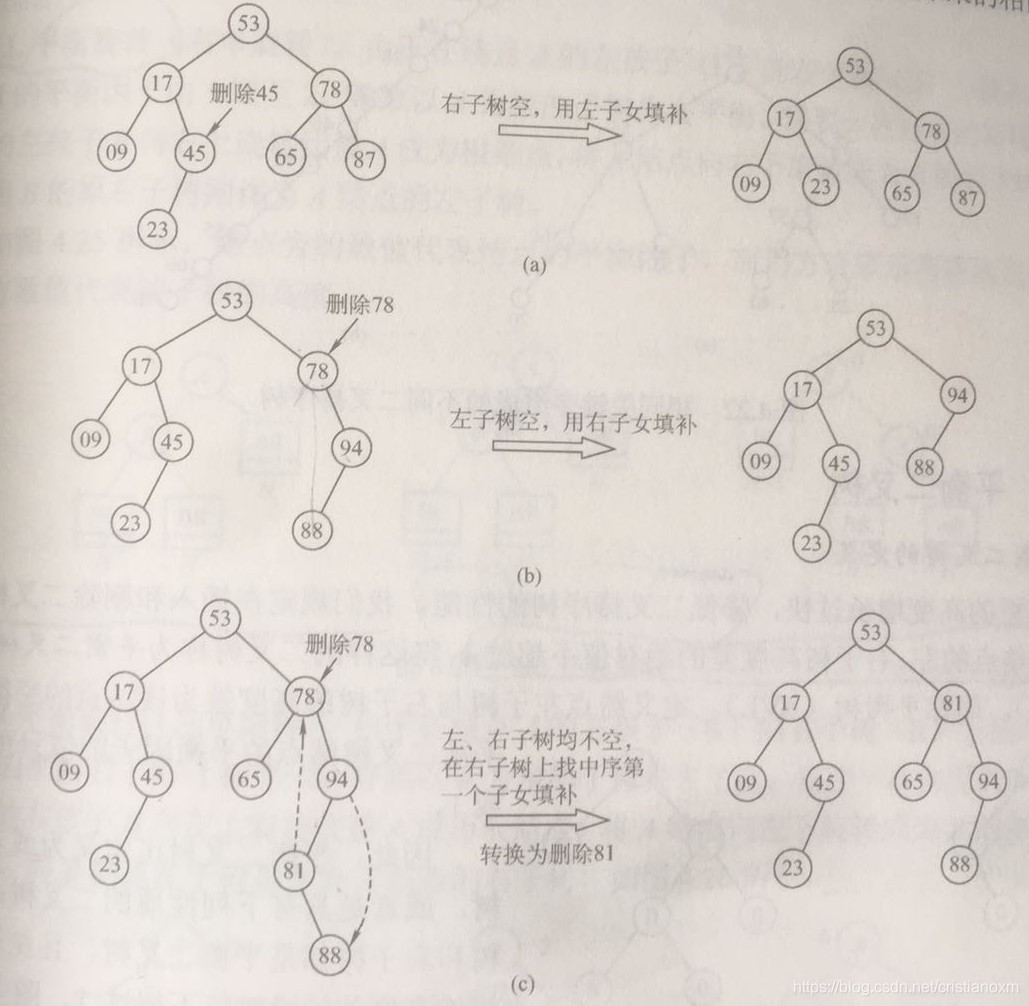
• （1）被删除的节点是叶子节点，则只需将它从其父节点中删除即可。
• （2）被删除节点 p 只有左子树，将 p 的左子树 添加成 p 的父节点的左子树即可；被删除节点 p 只有右子树，将 p的右子树添加成p 的父节点的右子树即可。
• （3）若被删除节点 p的左、右子树均非空，直至让其中序后继结点顶上去。
• 
  

代码：

1. 结点类

class TreeNode{
    public int data;
    public TreeNode left;
    public TreeNode right;
    TreeNode(int data){
        this.data=data;
    }
}

2. 树类
   插入结点：递归方式

  public boolean AddTreeNode1(TreeNode root, int data){
        TreeNode treeNode=new TreeNode(data);
        //树为空
        if(root==null){
            root=treeNode;
            return true;
        }
        //比根节点小，插入到左子树
        if(root.data>data){
            //当根结点左节点非空时，要继续递归插入 
            if (root.left == null) {
                root.left = treeNode;
                return true;
            } else {
                return AddTreeNode1(root.left, data);
            }
        }
        //比根节点大，插入到右子树
        else if (root.data < data) {
            //当根结点右节点非空时，要继续递归插入 
            if (root.right == null) {
                root.right = treeNode;
                return true;
            } else {
                return AddTreeNode1(root.right, data);
            }
        } else {
        }
            return false;
    }

查找结点

 public boolean SearchTreeNode(TreeNode root, int data){
        if(root==null){
            return false;
        }else if(root.data==data){
            return true;
        }else if(root.data>data){
            return SearchTreeNode(root.left,data);
        }else{
            return SearchTreeNode(root.right,data);
        }
    }

删除结点

public  boolean DeleteNode(TreeNode root, int data){
        //current为查找得到的节点
        TreeNode current=root;
        //parent为时刻更新父节点
        TreeNode parent=root;
        //tempParent为同时存在左右子树的迭代临时父节点
        TreeNode tempParent=root;
        //isLeft记录current节点的左右属性
        boolean isLeft=true;
        while(current.data!=data){
            parent=current;
            //到左子树查找
            if(current.data>data){
                isLeft=true;
                current=current.left;
            }else if(current.data<data){ //到右子树查找
                isLeft=false;
                current=current.right;
            }
            //查不到，返回false
            if(current==null) {
                return false;
            }
        }
        //第一种情况：删除节点为叶节点
        if(current.left==null && current.right==null){
            if(current==root) {
                root=null;
            }
            if(isLeft) {
                parent.left = null;
            }else{
                parent.right = null;
            }
            return true;
        }else if(current.right==null){    //第二种情况：删除节点只有左节点
            if(current==root) {
                root=current.left;
            } else if(isLeft) {
                parent.left=current.left;
            } else {
                parent.right=current.left;
            }
            return true;
        }else if(current.left==null){    //第三种情况：删除节点只有右节点
            if(current==root) {
                root=current.right;
            } else if(isLeft) {
                parent.left=current.right;
            } else {
                parent.right=current.right;
            }
            return true;
        }else{  //第四种情况：删除节点均存在左节点和右节点
            if(current==root){
                root=root.left;
            }
            TreeNode tempNode=current.left;
            //没有左节点
            if(tempNode.right==null){
                if(isLeft) {
                    parent.left=tempNode;
                } else {
                    parent.right=tempNode;
                }
            }else{  //存在左节点，迭代到最右侧子节点，即直接前驱
                while(tempNode.right!=null){
                    tempParent=tempNode;
                    tempNode=tempNode.right;
                }
                if(isLeft){    //为左节点，连接
                    parent.left=tempNode;
                    parent.left.left=current.left;
                }else{  //为右节点，连接
                    parent.right=tempNode;
                    parent.right.left=current.left;
                }
                //删除前驱节点，连接
                if(tempNode.left==null) {
                    tempParent.right=null;
                } else {
                    tempParent.right=tempNode.left;
                }
            }
            return true;
        }
    }

本文参考1
本文参考2