邻接矩阵存储无向图及遍历

#include "stdafx.h"
#include<iostream>  
#include<string>  
using namespace std;

//下面是循环队列模版  
template<class T>
class My_queue;

template<class T>
class Node
{
private:
    T data;
    Node<T> *next;
public:
    Node()
    {
        next = 0;
    }
    Node(T d)
    {
        data = d;
        next = 0;
    }
    friend My_queue<T>;
};

template<class T>
class My_queue
{
private:
    Node<T> *tail;
public:
    My_queue()
    {
        tail = new Node<T>();
        tail->next = tail;
    }

    ~My_queue()
    {
        clean();
        delete tail;
    }

    bool empty()
    {
        return (tail->next == tail);
    }

    void push(T d)
    {
        Node<T> *p = new Node<T>(d);
        p->next = tail->next;
        tail->next = p;
        tail = p;
    }

    T front()
    {
        if (empty())
        {
            cout << "queue is empty!" << endl;
            exit(0);
        }
        Node<T> *p = tail->next;
        T data = p->next->data;
        return data;
    }

    T back()
    {
        if (empty())
        {
            cout << "queue is empty!" << endl;
            exit(0);
        }
        T data = tail->data;
        return data;
    }

    void pop()
    {
        Node<T> *p = tail->next;
        Node<T> *q = p->next;
        p->next = q->next;
        if (q == tail)
            tail = p;
        delete q;
    }

    void clean()
    {
        Node<T> *p = tail->next;
        Node<T> *q = p->next;
        while (q != p)
        {
            p->next = q->next;
            delete q;
            p->next = q;
        }
    }
};

#define MAX_VERTEX_NUM 20  

bool visited[20];//全局数组，用于辅助遍历  

struct MGraph
{
    string vexs[MAX_VERTEX_NUM];//顶点数组  
    int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邻接矩阵  
    int vexnum;//顶点数目  
    int arcnum;//边数目  
};

int Locate_Vex(MGraph G, string x)  //用于确定顶点在顶点数组中的位置  
{
    int k;
    for (k = 0; G.vexs[k] != x; k++);
    return k;
}

void CreateUDN_MG(MGraph &G)
{
    //采用邻接矩阵表示法，构造无向图  
    int i, j, k;
    cout << "输入图的顶点数和边数：";
    cin >> G.vexnum >> G.arcnum;
    cout << "输入各个顶点的名称：";
    for (i = 0; i<G.vexnum; i++)
        cin >> G.vexs[i];

    for (i = 0; i<G.vexnum; i++)
        for (int j = 0; j<G.vexnum; j++)
            G.arcs[i][j] = 0;
    //上面是初始化邻接矩阵  

    for (k = 0; k<G.arcnum; k++)
    {
        cout << "输入每条边对应的两个顶点：";
        string v1, v2;
        cin >> v1 >> v2;
        i = Locate_Vex(G, v1);
        j = Locate_Vex(G, v2);
        while (i<0 || i>G.vexnum - 1 || j<0 || j>G.vexnum - 1)
        {
            cout << "结点位置输入错误,重新输入: ";
            cin >> v1 >> v2;
            i = Locate_Vex(G, v1);
            j = Locate_Vex(G, v2);
        }
        G.arcs[i][j] = 1;
        G.arcs[j][i] = G.arcs[i][j]; //置对称边  
    }
    cout << "图构造完成" << endl;
}

void DFS(MGraph G, int v)
{
    visited[v] = true;
    cout << G.vexs[v] << "  ";
    for (int j = 0; j<G.vexnum; j++)
        if (G.arcs[v][j] && !visited[j])
            DFS(G, j);
}

//深度优先遍历图  
void DFS_Traverse(MGraph G)
{
    //visited数组用来作为是否已访问的标志  
    for (int i = 0; i<G.vexnum; i++)
        visited[i] = false;
    for (int v = 0; v<G.vexnum; v++)
        if (!visited[v])
            DFS(G, v);
}

//广度优先遍历  
void BFS_Traverse(MGraph G)
{
    My_queue<int> q;
    int u, w, v;
    for (v = 0; v<G.vexnum; v++)
        visited[v] = false;
    for (v = 0; v<G.vexnum; v++)
        if (!visited[v])
        {
            visited[v] = true;
            cout << G.vexs[v] << "  ";
            q.push(v);
            while (!q.empty())
            {
                u = q.front();
                q.pop();
                for (w = 0; w<G.vexnum; w++)
                    if (G.arcs[u][w] && !visited[w])
                    {
                        visited[w] = true;
                        cout << G.vexs[w] << "  ";
                        q.push(w);
                    }
            }
        }
}

int main()
{
    MGraph G;
    CreateUDN_MG(G);
    cout << "深度优先遍历图为：";
    DFS_Traverse(G);
    cout << endl;
    cout << "广度优先遍历图为：";
    BFS_Traverse(G);
    cout << endl;
    return 0;
}

测试结果：

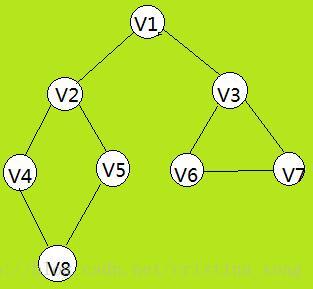
输入图的顶点数和边数：8 9  
输入各个顶点的民称：v1 v2 v3 v4 v5 v6 v7 v8  
输入每条边对应的两个顶点：v1 v2  
输入每条边对应的两个顶点：v1 v3  
输入每条边对应的两个顶点：v2 v4  
输入每条边对应的两个顶点：v2 v5  
输入每条边对应的两个顶点：v4 v8  
输入每条边对应的两个顶点：v5 v8  
输入每条边对应的两个顶点：v3 v6  
输入每条边对应的两个顶点：v3 v7  
输入每条边对应的两个顶点：v6 v7  
图构造完成  
深度优先遍历图为：v1  v2  v4  v8  v5  v3  v6  v7  
广度优先遍历图为：v1  v2  v3  v4  v5  v6  v7  v8  
Press any key to continue