JZOJ4868. 【NOIP2016提高A组集训第9场11.7】Simple

Description

Data Constraint

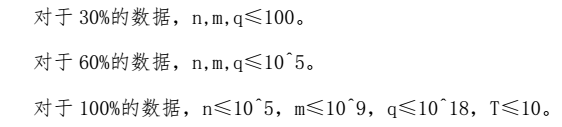
Solution

方法一：我们先来看一下不考虑重复时的的做法，对于一个固定的x，y的取值范围明显是[0,$\lfloor{{c-n*x}\over{m}}\rfloor$]。所以我们枚举x，就可以算出对应的值。ans=$\sum_{x=0}^{\lfloor{q\over{n}}\rfloor}{\lfloor{{c-n*x}\over{m}}\rfloor}$这也是我考场的做法，但这并没有考虑重复的情况，所以是不对的。

现在我们来想想该如何去重。我们知道，当x>$\lfloor{{m}\over{gcd(n,m)}}\rfloor$时，我们是可以将x减去$\lfloor{{m}\over{gcd(n,m)}}\rfloor$，然后y加上$\lfloor{{n}\over{gcd(n,m)}}\rfloor$，这样x又会再次小于$\lfloor{{m}\over{gcd(n,m)}}\rfloor$，与原来计算过的状态重复，这才导致了上面第一个算法时重复的情况，所以我们只要将x的范围缩小到[0,$\lfloor{{m}\over{gcd(n,m)}}\rfloor$]即可，即ans=$\sum_{x=0}^{\lfloor{{m}\over{gcd(n,m)}}\rfloor}{\lfloor{{c-n*x}\over{m}}\rfloor}$。注意一下，在x=0时，ans要减一个1，因为不能出现x，y都为0的情况。

方法二：其实这条式子n*x+m *y=c，我们可以转化成n *x+（a *n+i）=c的形式。所以我们设出d[i]表示存在一个最小的m *y，使$(m*y)Mod n=i$。那么对于一个d[i]，显然$d[(d[i]+m)Mod n]<=d[i]+m$，根据这条不等式，我们可以跑一下最短路，最后ans=$\sum_{x=0}^{n-1}{\lfloor{q-d[x]\over{n}}\rfloor}$

Code

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
ll n,m,q,i,t,j,k,l,ans;
int gcd(ll a,ll b){
    ll r=a%b;
    while (r) a=b,b=r,r=a%b;
    return  b;
}
int main(){
//  freopen("simple.in","r",stdin);freopen("simple.out","w",stdout);
    freopen("data.in","r",stdin);
    scanf("%lld",&l);
    while (l){
        scanf("%lld%ld%lld",&n,&m,&q);
        ans=q;
        if (m>n) swap(n,m);
        t=m/gcd(n,m);
        for (i=0;i<t;i++){
            if (n*i>q) break;
            ans=ans-(q-n*i)/m;
            if (i) ans--;
        }
        printf("%lld\n",ans);
        l--;
    }
}