[Learning-from-data]有限假设空间的可学性

本文链接：https://blog.csdn.net/csdn0006/article/details/84979642

本文探讨了机器学习中的可学性问题，重点在于有限假设空间下的学习模型。首先，介绍了学习的基本概念，强调了从数据中学习的重要性。接着，通过感知机模型展示了在数据集上学习的可能性，解释了学习算法如何通过迭代找到最佳解。讨论了学习与设计的区别，并指出学习的可行性在于能否从有限数据中推断全局信息。最后，引入概率理论，通过Hoeffding不等式证明了有限数据集如何提供对未知数据的预测能力，从而证明了学习的可行性。文章还讨论了学习的两个关键问题：如何保证在训练集和未见数据上的表现以及如何选择合适的假设空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

明白机器学习中的通用理论,然后在细化到数学推导,之后再明白局限性以及改进;辅助以代码.
笔记.防止看得太过于枯燥.

-What is learning?
-Can a machine learn?
-How to do it?
-How to do it well?
-Take-home lessons.

“学习”

我们人类的学习过程,有时候并不是直接从定义学习,更像是实例学习,比如说小孩学习"树",并不能给出一个真正的定义,而是从实例的树来学习这个定义,也就是说"learning from data".

Learning from data: 因为不能给出一个明确的解析解,但是可以从大量的数据中构建一个经验解决方法.换句话说,就是我们不能给出明确的定义,但是可以从大量的数据中归纳出一种解决方法. 一种归纳推理:从特殊到一般. learning from data.

Learning from data is used in situations where we don’t have an analytic solution, but we do have data that we can use to construct an empirical solution.

什么是学习?给出与"学习"相关的各种概念,目前为止出现的各种学习方法.

学习问题

这种学习方法learning from data 是 machine 尝试以自己的角度从数据中学习,机器"自己"理解的角度/方法,当然这种方法对人类而言,可能是"天书",but it works, it’s enough! 不需要人类理解.

学习的"成分"

数据记录x
记录标签y
数据集X
标签Y
目标函数f: 理想函数
学习函数g: 学习到的函数
假设空间H
理想情况下 g = f, 我们学到的g函数和理想函数f完全相同; 一般情况下,就是用训练学习到的函数g去逼近ideal target function理想函数f.

函数g的选择依据是:在训练数据集上g已经非常逼近期望函数f了,而且我们也希望在unseen data/新数据上也能逼近函数f,也就是说在新数据上也能"完美运行/不出错[判断出错]",没有误差. 但这个期望能否实现需要继续判断.

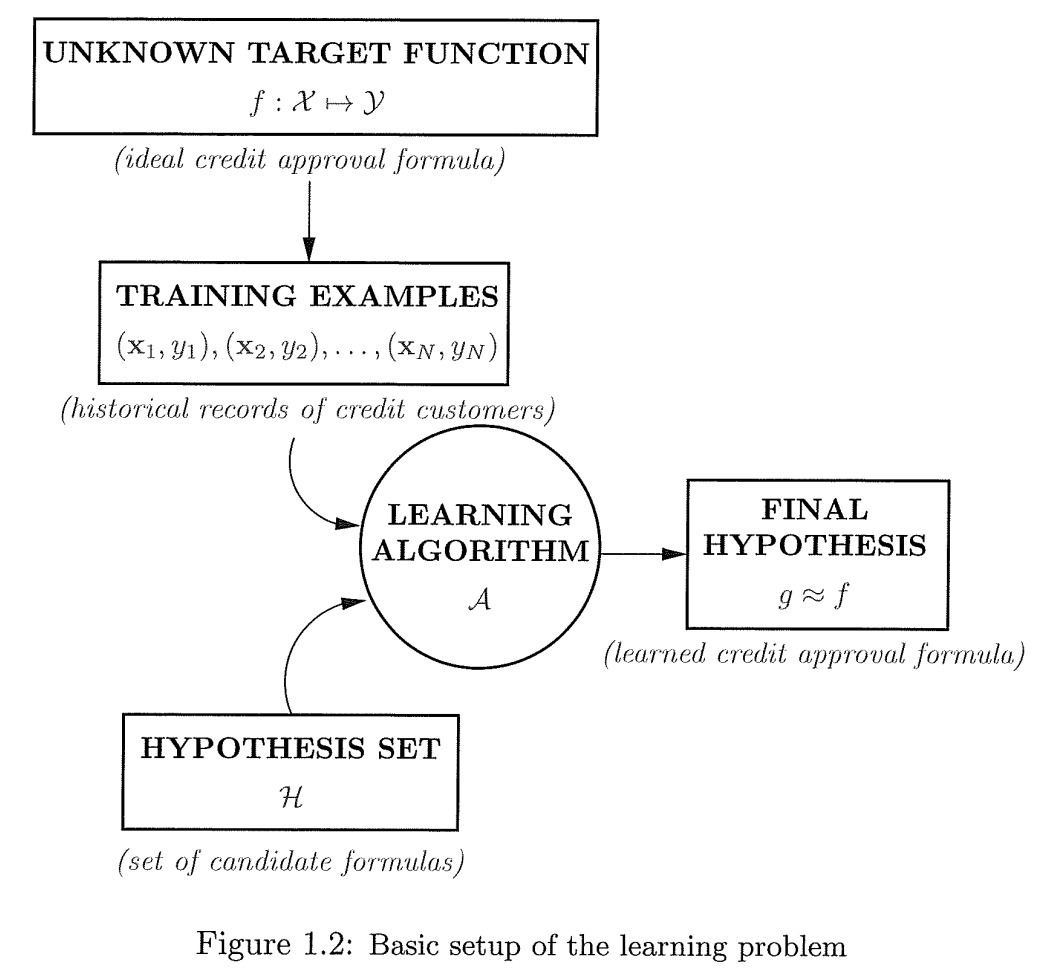
图中定义了"学习"过程中的各个"成分".

There is a target to be learned, but it’s unknown to us. We have a set of examples generated by the target. The learning algorithm uses these examples to look for a hypothesis that approximates the target.

一个简单的学习模型

对于一个实际的学习问题来说, 期望的目标函数f和数据集X能通过待求解的问题得到,是已知的[尽管目标函数并不是真正的已知],但是学习算法以及函数假设/假设函数是未知的,但是存在很多种选择需要我们自己选定. 假设函数集/函数空间和学习算法可以理解为"算法模型".

对于垃圾邮件分类器,如果数据集线性可分,那么我们能找到一个完美的模型:正确划分所有训练数据. 对于2-d维度来说,感知机模型的分类边界是一条直线.

假设空间H:

${h|Y=h_{\theta}(X), \theta \in R^n}$

假设空间由 $\theta$ 参数定义的一个函数族[实现确定了选定那种类型的算法].

感知机模型:

$h(x) = sign(w^Tx)$

分类结果是{+1, -1}.从式子中可以看出,分类结果是由两个向量内积决定,图像化来说就是两个向量的夹角决定,如果夹角大于90度,分为负类;夹角小于90度,分为正类.

PLA(perceptron learning algorithm):基于数据对感知机模型参数w进行学习.具体来说:
假设数据集线性可分,那么一定能找到一个超平面[参数向量w决定]将所有训练数据集中记录正确划分,也就是说,对于训练集中所有数据有h(xn)=yn.

PLA是一个简单的迭代算法:最终的分类效果是对训练数据集"完美划分".既然是一个迭代过程,刚开始划分效果并不好,需要进行优化,但是如何优化呢?或者说优化方法是什么?PLA给出了具体的方法.

在每次迭代t,t=0,1,…,当前迭代的权重向量为w(t). 训练集 $x_1,y_1),(x_2,y_2),...,(x_N,y_N)$ .
在训练集D中找一个误分样本点(x(t), y(t)),使用这个误分样本点对当前的权重向量w(t)进行更新.既然是误分,可以知道 $\neq sign(w^T(t)x(t))$ . 更新规则:
$w (t + 1) = w (t) + y (t) x (t)$ .

因为是误分样本,所以有上面的不等关系,在具体来说,就是正类样本分成负类,负类分成正类;

对于第一种情况来说,y(t)=1,但是感知机h(x)分成负类,因此 $w^Tx$ 两个向量内积应该是负的,本来夹角应该是小于90度的,但由于当前权重向量不准确,导致夹角大于90度了,对于这种情况需要两个向量之间的夹角变到90度里,所以让 $w (t + 1) = w (t) + x (t)$ ,两个起点相同的钝角向量相加,结果[w(t+1)]和原来的向量x(t)之间的夹角变到90度里,因此更新后的超平面能对这个样本点正确分类了;

对于情况二,y(t)=-1,但是h(x)分成正类,从图象上来说,本来两个钝角向量,变成了锐角向量,我们需要做的就是让锐角变到钝角去,从上面的例子中得到启发,两个起点相同的锐角向量[相减],$w(t+1) = w(t) - x(t)结果为更新后的权重向量w(t+1),此时两个向量的夹角成了钝角,也就是说超平面能对这个样本点(x(t),y(t))正确分类了.

两种情况合二为一,更新规则变成:

$w (t + 1) = w (t) + y (t) x (t)$ .

符合两种误分情况的更新方法.同时从上面的更新方法来看,每次更新只选择一个误分样本点.但最终一定会得到一个"完美"的模型.并且这个结果和我们如何初始化w,如何选择误分样本无关.因为一定有一个"最优解".

这种学习算法在无限的解空间里通过有限步的迭代最终找到了最优解,求解过程并不是无限次的使用每种可能进行尝试,而是有目的性的优化.找准优化方向是根本,只有方向正确,最终一定能找到.

BUT,关于这个学习模型还存在一定的疑问?

数据集D上学到的模型g对于unseen data是否适用?[学习理论的关键问题–模型的泛化评估]
如果数据集D上的样本点不是线性可分呢?应该怎么办?

**为什么一定能算法收敛?**一定能找到一个最优解,证明PLA算法的更新规则是正确的.

http://www.cnblogs.com/HappyAngel/p/3456762.html#top

**如果数据线性不可分怎么办?**能否通过PLA变形,完成问题求解.

http://www.cnblogs.com/HappyAngel/p/3456762.html#top

Learning VS. Design

Learning是基于数据进行学习的, design更像是专门设计的,由专家定义设计,有大量的专业知识[先验知识].design方法并不需要数据,不需要从数据中获取信息.

"学习"的可行性

How could a limited data set reveal enough information to pin down the entire target function?
有限的训练数据集为什么能从中学到整个数据集上的通用信息???或者说为什么有限集上学到的模型能在未知数据上应用?难道不会出错吗?

一个例子

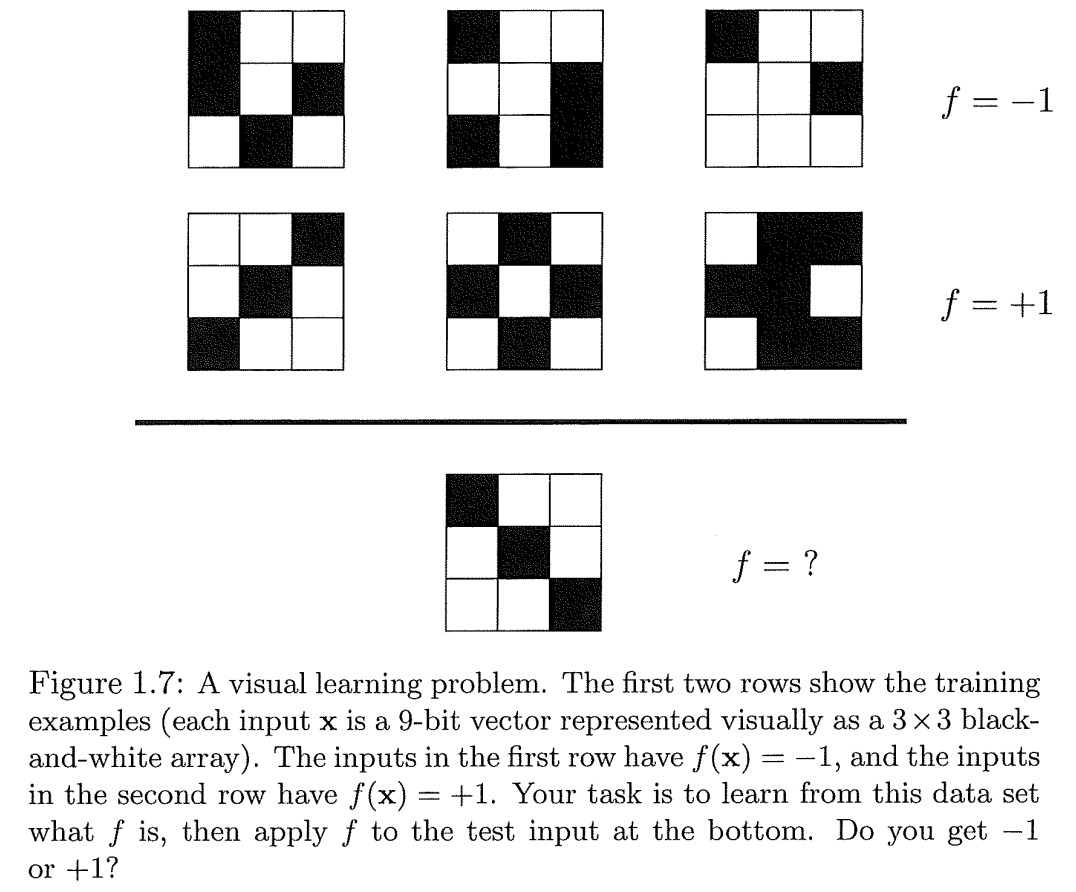
从上面的例子可以看出,对于6个样本的数据集来说,学到的模型并不一致,但是在数据集里,模型能完美运行,数据集之外unseen data上,不同的模型有不同的预测结果.但是我们并不能判断到底哪个结果是正确的[缺少额外信息]? 这个例子从一定程度上表明了判断"学习可行性"的难度.

Outside the Data Set

当我们在训练数据集D上进行训练时,表现良好,但在数据集之外unseen data上一无所知,这并不是学习,这属于单纯的记忆.我们关心的是模型在数据集之外的unseen data上的表现如何?

Does the data set D tell us anything Outside of D that we didn’t know before? If the answer is YES, then we have learned something. If the answer is NO, we can conclude that learning is not feasible.
训练数据集D,能够揭示数据集D之外的我们不知道的整个数据空间X上的信息?如果可以,那么机器学习就可行,能在有限集D上学到的知识是全局的,具有普世性[迁移性];如果不能揭示全局信息,机器学习就没有意义.

The performance outside D is all that matters in learning.

如何证明D上学到的f能够和全局h相互接近,这样,就可以用f来代替h,来进行应用.

Probability to the Rescue

We will show that we can indeed infer something outside D using only D, but in a probabilistic way.虽然推断的函数和全局target函数f相比可能并不完全相同,但关键是我们使用一种方法能预测数据集D之外unseen data上的表现如何.一旦确定了这种方法,我们就可以扩展到一般性的学习问题上,并能确定什么是可以学习的,什么是不能学习的?

举一个简单的例子,一个有红色和绿色石头的无限大瓶子[不能穷举石头个数],瓶子中红色石头和绿色石头的比例,如果在瓶子中随机选择一块石头,红色石头的概率是 $\mu$ ,绿色石头的概率 $1-\mu$ . 我们假定 $\mu$ 对于我们来说是未知的.