二叉查找(搜索)树（详解 + 刷题）

千帐灯无此声

已于 2024-05-09 09:23:10 修改

阅读量1.8k

点赞数 22

分类专栏： # 《算法训练营入门篇》文章标签：数据结构算法

于 2024-01-30 21:24:46 首次发布

本文链接：https://blog.csdn.net/csdner250/article/details/135872473

版权

《算法训练营入门篇》专栏收录该内容

15 篇文章

订阅专栏

本文介绍了二叉搜索树的基本概念、查找、插入、创建过程以及删除节点的分类讨论，包括查找时间复杂度、插入操作和删除的复杂度分析。同时提到了ACmap和TTL直接排序的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

🌼前言

嘿嘿嘿嘿嘿~ 《算法训练营入门篇》 ---- 完结撒花 *★,°*:.☆(￣▽￣)/$:*.°★*

本篇博客，作为《算法训练营》的结束，后续的：

平衡二叉树(红黑树) + 启发式搜索 -- 面试不考，二分 + DFS + BFS -- 学过了

（剩下就是加大题量，提高熟练度的问题）

下一步，考虑到大二下暑期实习的迫切性

蓝桥杯辅导课不跟了（已跟一半多），先一刷 hot100（剑指offer比较简单，也先放放）

有时间就二刷........

🌼二叉搜索树

🌙前置知识

二叉查找树 = 二分 + 二叉树

融合了两者的优势，二分的高效查 + 二叉树的高效增删改

二叉查找树（Binary Search Tree）BST，又二叉搜索树，二叉排序树

其 中序遍历，是递增序列，因为左子树 < 根 < 右子树

🎂查找

时间复杂度 O(logn)，n 为元素个数，logn 为二叉树高度

BSTree Search(BSTree T, ElemType key) { // 递归
    // 查找成功 - 返回指向该元素的指针，失败返回空指针
    if ( (!T) || key == T->data ) 
        return T;
    else if (T->data > key)
        return Search(T->lchild, key); // 递归左子树
    else 
        return Search(T->rchild, key); // 查找右子树
}

🌳插入

时间复杂度 O(logn)，即查找插入位置的时间复杂度 + 插入只需要常数时间（忽略）

void Insert(BSTree &T, ElemType e) { 
    // T 不存在大小为 e 的元素，就插入
    if (!T) { 
        BSTree S = new BSTNode; // 新节点S
        S->data = e;
        S->lchild = S->rchild = NULL; // S 作为叶子节点
        T = S; // 新节点更新到树中
    }

    else if (T->data > e) 
        Insert(T->lchild, e); // 插入左子树
    else
        Insert(T->rchild, e); // 插入右子树
}

🐕创建

步骤

（1）初始化空树， T = NULL

（2）输入 x，将 x 插入到二叉查找树 T

（3）重复 2，直到输入完毕

代码

void Create(BSTree &T) {
    // 依次读入元素 e，并插入
    T = NULL; // 初始化空树
    ElemType e;
    cin >> e;
    while (e != ENDFLAG) { // ENDFLAG 自定义常量，输入结束标志
        Insert(T, e); // 元素 e 插入 T
        cin >> e;
    }
}

分析

二叉查找树创建，需要 n 次插入

每次插入时间复杂度 O(logn)

平均复杂度 O(nlogn)

相当于把无序序列，转换为一个有序序列

创建二叉搜索树，和快排一样

根节点 == 快排中基准元素

左右两部分划分，取决于基准元素

🌼删除

分类讨论

（1）

被删除节点 P，左子树为空 --> 右子树取代 P 的位置

再重新连接

（2）

被删除节点 P，右子树为空 --> 左子树取代 P 的位置

再重新连接

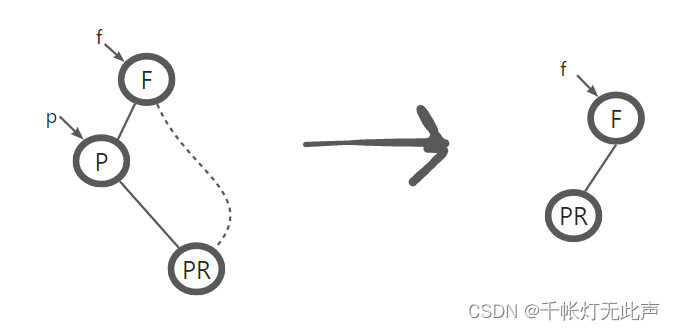
（3）

被删除节点 P，左右子树，都存在

则需要 P 的直接前驱 OR 直接后继，取代 P 的位置

然后删除直接前驱 s

最后将前驱节点的某个孩子重新连接到前驱节点的父亲上

直接前驱 s：左子树的最右节点（即，比 P 小的最大节点）

直接后继 s：右子树的最左节点（即，比 P 大的最小节点）

之所以这样选取节点，为了保证删除 -- 取代后，二叉搜索树的有序性

代码

删除的时间复杂度 O(logn)

查找被删除节点为O(logn)

如果删除时，需要找到直接前驱，也需要O(logn)的时间

所以总的时间复杂度 O(logn)

以下代码是直接前驱的 --> 左子树的最右(大)节点

void Delete(BSTree &T, char key) {

    // 二叉搜索树 T 中删除 值为 key 的节点
    BSTree p = T; // p 待删除节点
    BSTree f = NULL; // f 是 p 的父亲
    BSTree q, s; // s 直接前驱, q 是 s 父亲

    if (!T) return; // 树为空
    
    // 查找待删除节点 p
    while (p) {
        if (p->data == key) break; // 找到了
        f = p; // f 为 p 父亲
        if (p->data > key)
            p = p->lchild; // 左子树
        else
            p = p->rchild; // 右子树
    }
    
    if (!p) return; // 找不到

    // 3 种情况：左右子树都有，无左，无右
    if ( (p->lchild) && (p->rchild) ) {
        q = p; // q 是 s 父亲
        s = p->lchild; // s 是直接前驱
        while (s->rchild) { // 比 p 小的最大的点
            q = s;
            s = s->rchild;
        }
        // s 赋值给 p
        p->data = s->data;
        // 删除 s，只需要将 s 的左右孩子赋给 父亲 q 
        if (q != p)
            q->rchild = s->lchild; // 重接 直接前驱s 左子树
        else
            q->lchild = s->lchild; // 重接 右子树（s 只有左子树）
        delete s;
    }

    // 无左 或 无右子树
    else {
        // 被删除节点 p 无右，重接 p 左节点 PL
        if (!p->rchild) {
            q = p; // q 待删除节点
            p = p->lchild;
        }
        else { // 无左孩子
            q = p;
            p = p->rchild;
        }
        // p 的子树挂到 p父亲 f 的对应位置
        if (!f) // p 根节点, 没有父亲
            T = p; // T 即根节点
        else if (q == f->lchild)
            f->lchild = p;
        else
            f->rchild = p;
        delete q;
    }
}

🌙刷题

（一）落叶

1577 -- Falling Leaves (poj.org)

题目

输入删除序列，输出先序序列

样例

👆删除序列

思路

需要根据输入的树叶🍃删除序列，构造二叉搜索树👇

（大写字母；* 分隔每一组测试；$ 结束输入）

（1）删除序列，最后一个字母为树根、

（2）先输入的字母更深，所以逆序建树

解释下，为什么先输入的更深，就要逆序建树 (反着输入) 呢？

1) 逆序是为了，让更接近根节点的，先插入，有利于构建更平衡的二叉搜索树

2) 如果此时，顺序建树，可能会形成链表一样的不平衡二叉树，极大降低效率

（3）字符串存储读入序列，接着，逆序创建二叉树（小的字母插入左子树，大的右子树）

（4）输出先序遍历（根 - 左 - 右）

AC 代码

#include<iostream>
#include<cstring> // memset()
using namespace std;

int cnt = 1; // 计数

struct node {
    int l, r; // 左/右儿子索引
    char c; // 节点字符
}tree[110]; // 存储二叉树

void Insert(int k, char ch) // 索引 k 出发, 插入字符 ch
{
    if (!tree[k].c) { // 当前节点为空, 直接插入
        tree[k].c = ch;
        return;
    }
    if (tree[k].c > ch) { // 左子树找
        if (!tree[k].l) { 
            tree[++cnt].c = ch; // 赋值
            tree[k].l = cnt; // 连接
        }
        else 
            Insert(tree[k].l, ch); // 左儿子不为空，递归左子树
    }
    else if (tree[k].c < ch) { // 右子树找
        if (!tree[k].r) {
            tree[++cnt].c = ch;
            tree[k].r = cnt;
        }
        else
            Insert(tree[k].r, ch); 
    }
}

void pre_order(int k) // 先序遍历, k 索引
{
    if (!tree[k].c) return; // 当前节点为空
    cout << tree[k].c; // 输出字符
    pre_order(tree[k].l); // 递归左子树
    pre_order(tree[k].r); // 递归右子树
}

int main()
{
    string s, s1;
    while (1) { // 多组输入
        s = ""; // 初始化空字符串
        memset(tree, 0, sizeof(tree)); // 初始化结构体数组
        while (cin >> s1 && s1[0] != '*' && s1[0] != '$')
            s += s1; // 得到树叶删除序列
        // 逆序建树
        for (int i = s.size() - 1; i >= 0; --i) { // 第一次死循环, 写成++i了
            Insert(1, s[i]); // 1 表示从根节点出发
        }
        pre_order(1); // 根节点 1 开始
        cout << endl;
        if (s1[0] == '$') break;
    }
    return 0;
}

虽然，但是，题目好像没体现，如果输入相同字母怎么处理，按代码来看，应该是直接舍弃

（二）完全二叉搜索树

2309 -- BST (poj.org)

解释

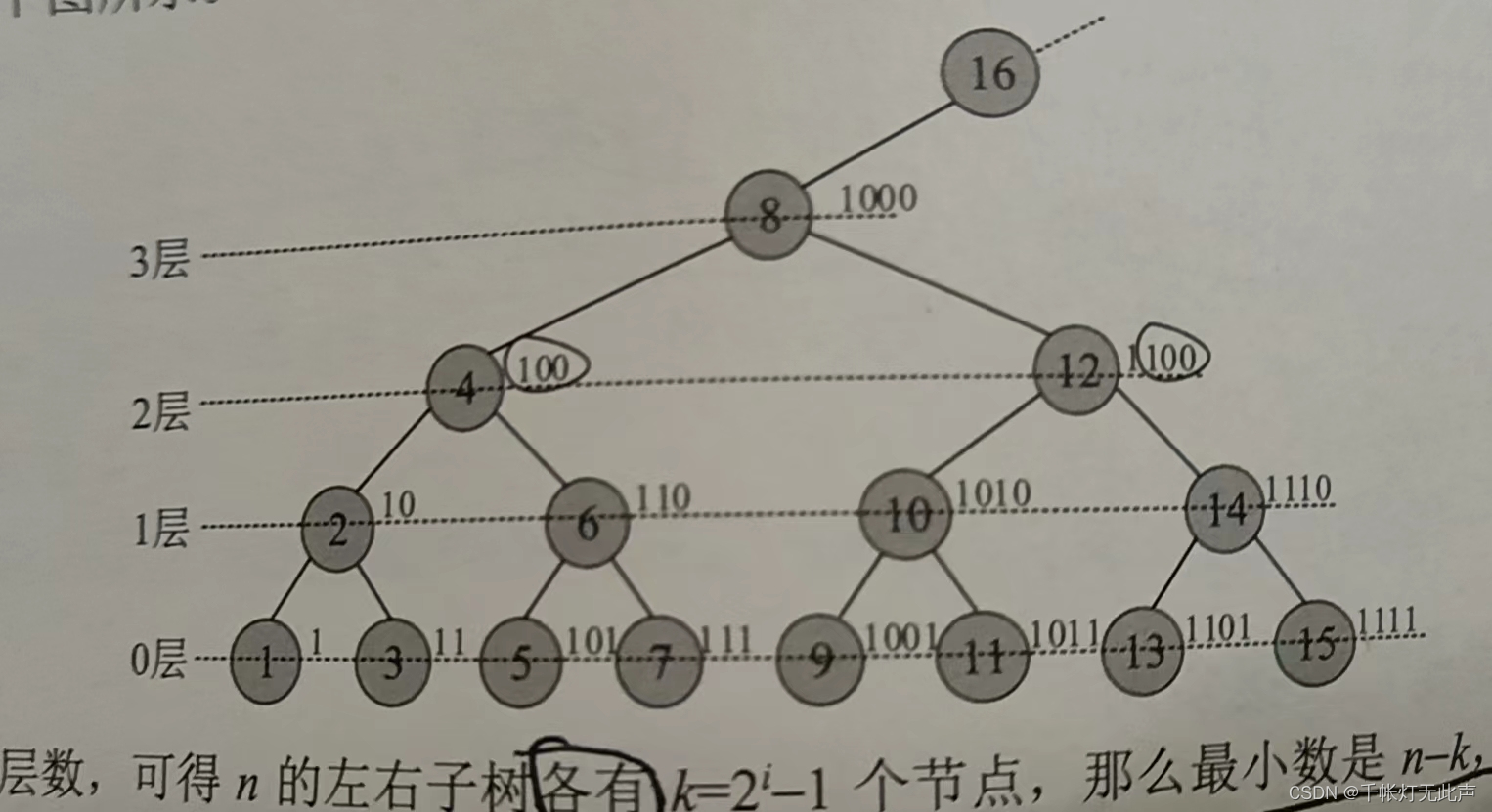
（1）看图找规律

若给定的 n 是奇数，必定是叶子节点，比如 1 3 5 7... 那么最大数和最小数都是自己

（2）

否则，求 n 所在的层数（底层为 0 层）

（3）

层数，即 n 这个数，二进制表示中，从低位开始第一个 1 的位置

（4）

比如 6 的二进制 110，是第 1 层

比如12 的二进制 1100，是第 2 层

（5）

令 i 为层数，那么 n 的左右子树，各有，k = 2^i - 1 个节点

比如 12 ，第 2 层，k = 2^2 - 1 = 3，所以 12 的左右子树各有 3 个节点

最小数即 n - k，最大数 n + k

12 的最小数就是 12 - 3 == 9，最大数 12 + 3 == 15

（6）

那么如何从 n 得到 k 的值呢？👇

n 取反，再 +1 ，得到的数，和原数 n 比，低位开始，直到第一个 1 ，都一样

后面都相反，即 -n

（7）此时再用 -n & n 即可得到 2^i

-n 即补码，按位取反 + 1

不理解的看看这个👇

【位运算】深入理解并证明 lowbit 运算_define lowbit(x) ((x) & - (x))-CSDN博客

AC 代码

#include<iostream>
using namespace std;

#define lowbit(x) (x&(-x)) // 宏定义lowbit()函数

int main() 
{
    int N, n;
    cin >> N;
    while (N--) {
        cin >> n;
        int k = lowbit(n) - 1;
        cout << n - k << " " << n + k << endl;
    }
    return 0;
}

（三）硬木种类

2418 -- Hardwood Species (poj.org)

思路

读入多行带空格字符串，每个字符串代表一个种类

统计每个种类占总数百分比

方法 1)

map 键值对，按键的大小升序排序，然后输出

方法 2)

二叉搜索树，每个单词存入二叉搜索树，比较时，按字符串的字典序比较

最后输出中序遍历结果（二叉搜索树中序遍历升序）

关于 map

默认升序，也可通过👇第3个模板参数设置为降序

map<string, int>a; //升序
map<string, int, greater<string> >a; //降序

h[key] = val;
//等价于
h.insert(make_pair(key, val));

AC map

插入，删除的复杂度都是 O(logn)，自动排序，所以会比快排快很多

#include<iostream>
#include<map>
#include<string> // getline()
#include<cstdio> // printf()
using namespace std;

int main()
{
    int sum = 0;
    map<string, int> m; // 默认按键升序
    string s;
    while(getline(cin, s)) { // 带空格字符串
        m[s]++; // 插入键值对
        sum++; // 总数
    }
    // 迭代器访问 map
    for (map<string,int>::iterator it = m.begin(); it != m.end(); ++it) {
        cout << it->first << " ";
        printf("%.4f\n", it->second * 100.0 / sum);
    }
    return 0;
}

TTL 直接排序

超时，原因可能是sort() O(nlogn) 超时了，也可能是用 getline() 读入字符串？？

因为题目结尾提示要用 scanf()

#include<iostream>
#include<string> // getline()
#include<cstdio> // printf()
#include<algorithm> // sort()
using namespace std;

const int maxn = 1e6 + 10;
string m[maxn];

int main()
{
    int sum = 0, ans = 0; // sum 总数, ans 当前品种数量
    string s;
    while(getline(cin, m[sum])) // 带空格字符串
        sum++; // 总数
    sort(m, m + sum); // 升序
    for (int i = 0; i < sum; ++i) { // 遍历每一棵树, 边遍历边输出
        ans++;
        if (m[i] != m[i + 1]) {
            cout << m[i] << " ";
            printf("%.4f\n", ans * 100.0 / sum);
            ans = 0;
        }
    }
    return 0;
}

AC 二叉搜索树

C++ AC，G++ WA

#include<iostream> 
#include<cstdio> // printf()
#include<string> // getline()
using namespace std;

typedef struct node {
    string w;
    struct node *l, *r; // 类型都是 struct node
    int cnt;
}*nodeptr; // 类型别名

int sum = 0;
nodeptr br; // 根节点

void BSTinsert(nodeptr &root, string s) // 引用传递当前节点 root
{
    if (root == NULL) {
        nodeptr p = new node(); // 新节点
        p->l = NULL, p->r = NULL;
        p->w = s;
        p->cnt = 1; // 出现次数
        root = p;
    }
    else if (root->w == s)
        root->cnt++;
    else if (root->w > s)
        BSTinsert(root->l, s);
    else
        BSTinsert(root->r, s);
}

void midPrint(nodeptr root)
{
    if (root != NULL) {
        midPrint(root->l);
        cout << root->w << " ";
        printf("%.4f\n", root->cnt * 100.0 / sum);
        midPrint(root->r);
    }
}

int main()
{
    br = NULL; // 初始化
    string s;
    while (getline(cin, s)) {
        BSTinsert(br, s); // 插入
        sum++;
    }
    midPrint(br);
    return 0;
}

嘿嘿嘿嘿嘿~ 《算法训练营入门篇》 ---- 完结撒花 *★,°*:.☆(￣▽￣)/$:*.°★*