数位dp-递推迭代和记忆搜索法dfs

(本文为网上各资料结合自己理解所得，如有误，欢迎指出讨论交流。)

所使用题目为经典例题Windy数和3.28日腾讯笔试题(奇偶数题)。

储备知识：

数位概念：例如4368，个位数为8，十位数为6,...,这种个位数十位数就称为数位。当然如果将4368转为二进制1000100010000,那么这里的每一个0和1也称为数位。

一个小技巧：针对某一个数4368,要遍历全部不大于这个数的所有数。显然：首先最高位不能超过4，当最高位取1-3时，后面三个数位取啥都可以，当最高位取4时，第二高位就不能取超过3即此时第二高位只能取0-3，当第二高位取0-2时，后面两个数位取啥都可以，当第二高位取3时，第三高位就不能取超过6，...，以此类推。因此当我们在统计某个满足条件的不超过R的数时，自然是要在不大于R上寻找，因此这个小技巧十分重要。知道这个小技巧后，其实就知道我们要遍历怎样的数了。只有遍历了全部，你才能去判断这个数是不是满足题目条件。因此一定要理解如何遍历全体。当然上述和下图说明的都是遍历与4368同数位的数(即4位数的数),若还需找到4368小于四位数的则直接从第二高位开始1-9及后面都没有限制即可。

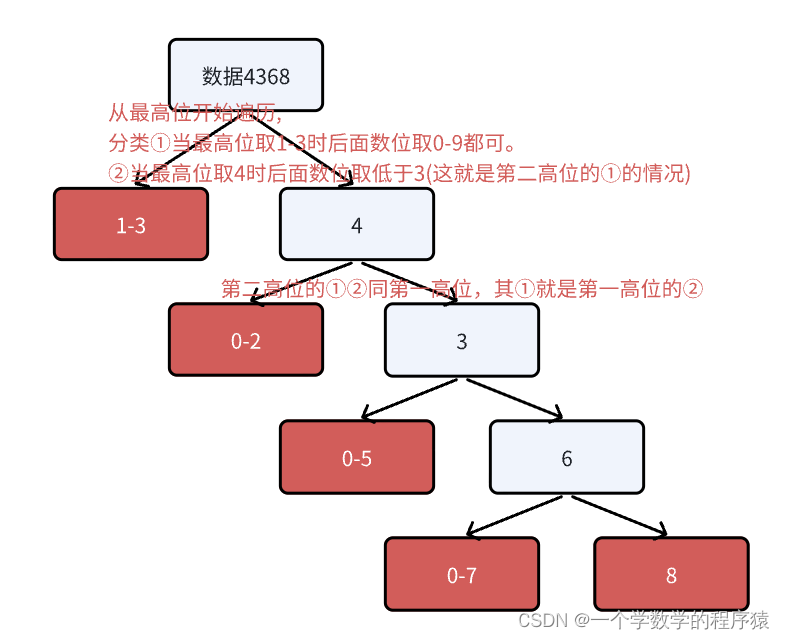
数位dp题目的特点：求某个数值区间[L,R]内，满足某种性质(可变)的数的个数。

eg.1. Windy数：求数值区间[L,R]内，满足相邻数之差不小于2的数的个数。

2. 3.28tx笔试题：求数值区间[L,R]内，满足数位中奇数个数与偶数个数相同的数的个数。

(其实注意到上面两个题虽然用同种方法，但其的数位dp数组会有本质区别，原因是由1.其满足条件的数只与数中的前后两个数字有关【求不降数也是如此】, 但是求2.其满足条件的数是与整个数的数字有关【求数之和为偶数/奇数/满足某个条件也是如此】，所以下面可以看看二者数位dp数组的变化。)

数位dp的技巧1：将求数值在[L,R]范围内的转化为求[0,L-1],[0,R], 这样可以将两个上界转为一个。

数位dp的技巧2(这也是整体思想,注意看)：无论对于递推迭代法还是dfs记忆化搜索，都是从最高位遍历到最低位，直至满足条件即退出(递推迭代法)或遍历到最后一数位就退出(dfs记忆化搜索法)。

=====================================================================

下面分别介绍这两种方法并用这两个例题进行说明。

一. 首先，采用递推迭代法。总体思想：首先构造数位dp数组，根据题目含义来构造二维dp或三维dp，一般题目条件若只与数字相邻有关的是构造二维，例如这里第1.题；与数字整体相关的要记录多个状态是构造三维，例如这里第2.题。

注意: ①其中前两维的含义一般dp[i][j]表示：i位数其中最高位为j(eg.i=3,j=3,则300-399之间)的（满足某个条件）的数的个数。②dp数组的递推公式即第i位数的推导一般都是由第i-1位数推导而来。③代码中a数组的意思是将输入的数字的上限传入数组中，方便提取。

1. Windy数：

# 给定数值[L,R],求在L-R之间的Windy数的个数。Windy数是相邻两个数之差不小于2的数。

# 因为本题涉及的条件只是 相邻两个数，因此dp数组考虑二维即可

# 初始化dp数组
def init(dp):
    # 首先题中只涉及到相邻两个数位的数的要求，并不涉及整个数因此二维dp即可
    # dp[i][j]表示i位数其中最高位为j(eg.i=3,j=3,则300-399之间)的Windy数的个数
    # 数位dp数组的递推关系:都是由dp[i-1][k]推导过来的，即第i位数都是由第i-1位数推过来。
    # dp[i][j] = dp[i-1][k] 其中abs(j-k)>2
    # 【对一位数的处理,或者说初始化dp数组】
    for j in range(10):
        dp[1][j] = 1
    # 【对大于2位数的处理】
    for i in range(2,N):
        # 注意这里j是从0开始，因为后面slove函数是使用dp数组与前一位进行拼接，因此大于2位数的可以从0开始
        for j in range(0,10):
            for k in range(10):
                if abs(j-k)>=2:
                    dp[i][j] += dp[i-1][k]
def slove(x):
    # 求[0,x]左闭右闭的Windy数的个数,若要求[l,r]的则只需slove(r)-slove(r-1)即可
    global a,dp
    res, last = 0, -2 # 这里last设定-2是因这样最高位数与上一位一定相差-2 则必定会符合条件地留下来
    cnt = 0
    while x:
        cnt += 1
        a[cnt] = x%10
        x//=10
    # 遍历不大于x的数位段，首先是同cnt位段(eg4368,则这里遍历的是1000-4368)
    # 因为要找小于等于的，按照前面将的逻辑，自然从高位到低位进行限制
    for i in range(cnt,0,-1):
        limit = a[i] # 提取当前位数字的限制
        for j in range((i==cnt),limit):
            # (i==cnt)是用的很巧妙，若当前就是最高位则从1开始，若当前不是最高位，则从0开始
            # 这里j取不到limit跟上图的树有关，如果取limit则下一位要限制，不取limit，则下一位的值不用限制，是两种情况，因此需要分开。
            # dp[i][j]已经提取完所有满足数位的Windy数的个数，solve函数的作用就是将其累加起来
            # 当前位数为i且最高位数为j的Windy数个数累加，
            # 例如4368，则1000~1999(dp[4][1])+2000~2999(dp[4][2])+3000~3999(dp[4][3])[至此一轮循环结束]
            # [第二轮循环当last取到4时就会进入第二轮循环]4000-4099(dp[3][0])+4100-4199(dp[3][1]),...,以此类推，直至+4368
            if abs(last-j)>=2:
                res+=dp[i][j]
        if abs(last-limit)<2:
            break # 若limit取不了则后面的不用看了直接剪枝
        last = limit # 否则继续取
        if i == 1:
            # 如果是最后一位数已经走到这 说明limit也是合适的需要自加1
            res += 1  # 4368是在这里加上的，有些题目条件并不需要加上
    # 遍历不大于x的<cnt位段，1-9(dp[1][1])+10-19(dp[2][1]+...
    for i in range(1,cnt):
        for j in range(1,10):
            res += dp[i][j]
    # 单独对0进行添加 这里只是为了与dfs方法统一，若不需要可不加
    res += dp[1][0]
    return res

if __name__ == '__main__':
    # 递推迭代法其实就两步
    # 预处理所有位数段的Windy数个数，使得遍历到时就可以直接提取--数位dp数组的初始化
    # 遍历num同等位数和以下位数的所有位数段，提取dp的值
    N = 20 # 数字数位
    dp = [[0]*10 for _ in range(N)]
    init(dp)
    # 初始化dp数组后，后面处理遍历到该数位段时都是从中进行取数
    num = 4368
    a = [0] * N
    print(slove(num))

2. tx笔试题：

def init(dp):
    # dp[i][j][k]的含义 i位数最高位为j.eg（i=3,j=3,则300-399）之间的奇数比偶数多k-N个的数的个数，当k==N时就是数位奇数与偶数相同。
    global N
    for j in range(10):
        # 针对一位数的初始化
        if j%2 == 0:
            dp[1][j][N-1] += 1
        else:
            dp[1][j][N+1] += 1
    # 从二位数开始，逐个由低位递推至高位进行初始化.eg.(10-19之间符合的数 是在固定的最高位为1(奇数的基础上)，将0-9对应的偶数个数加上)
    for i in range(2,N):
        for j in range(0,10):
        # 从二位数开始，首位也可以从0开始，因为后面solve时是对其进行拼接
            if j%2 == 0:
                for k in range(2*N - 1):
                    # 开始更新dp，因为j为偶数，因此k不可能为2*N - 1(即不可能全为奇数)
                    for x in range(10):  # 要由次高位的推导过来
                        dp[i][j][k] += dp[i-1][x][k+1] # 第二高位的奇数多1再加上当前位的j(是偶数)则奇数不会多1了
            else:
                for k in range(1, 2*N):
                    for x in range(10):
                        dp[i][j][k] += dp[i-1][x][k-1]
# 至此就初始化完dp数组
# 下面用slove函数来分类寻找dp数组
def solve(num):
    global a
    # 统计从1开始至num的所有数位为奇数与偶数个数相同的数字个数
    res, last = 0, N #，N表示刚好未累计
    # 更新a数组
    cnt = 0  # 用来更新a数组的指标 同时记录最高位
    while num:
        cnt += 1
        a[cnt] = num%10
        num//=10
    # cnt位的，从最高位开始
    for i in range(cnt,0,-1):
        # 从最高位到个数位
        limit= a[i]  # last来表示累计的奇数个数
        # 将每一位不超过limit的数先累计,不是最高位就可以从0开始，是最高位只能从1开始
        for j in range((i==cnt), limit):
            res += dp[i][j][last] # 这里后面的last赋值有巧妙之处
        # 当前位是都要的
        if limit%2 == 0:
            last += 1  # 如果limit为偶数，则last就多需要一个奇数
        else:
            last -= 1
        if i == 1 and last == N:
            # 如果i走到1了并且last也不差不多则剩余的那个数还是需要的
            res += 1
    # 答案小于cnt位的
    for i in range(1,cnt):
        # 数字共有i位的 且最高位的数字为j
        for j in range(1,10):  # 因为0必然不是结果 如果是则可以单独拿出来讨论
            res += dp[i][j][N]
    return res

if __name__ == '__main__':
    # 先预处理数位dp，找出所有位数的dp对应值
    # 构造slove函数，来找到对应的dp值进行相加，分类讨论进行相加
    # [L,R]的结果就是[1,R]-[1,L]的结果
    # 初始化需要用到的a数组(存储每一数位的上限)
    # 以及初始化dp数组
    # 根据本题，dp数组的含义dp[i][j][k]表示i位数最高位为j奇数比偶数多k-N个的个数。eg如果i为3，j为3，则表示的是
    # 300-399这一段的数字中奇数数位比偶数数位多k-N的个数。
    N = 20 # 根据题目条件，这里设定题目中的数字数位的最高位为19
    a = [0]*N
    dp = [[[0]*(2*N) for _ in range(10)] for _ in range(N)]
    init(dp)
    num = 4368
    print(solve(num))

二. 采用记忆化搜索法。

        记忆化搜索本质上先是利用dfs暴力搜索发现有多余的步骤，因此加入了记忆化的数位dp数组来记录之前搜过的状态的值，就可以避免多次重复搜。下面讲一下这个过程。(这个数位dp数组的定义与递推法的会有不同，这个数位dp数组会体现记忆性，也只是体现记忆性，并没有递推公式.因此或许这就是叫记忆化搜索原因所在(这个我瞎说的但觉得可以这样理解))

首先，如果是dfs暴力搜索，显然这道题目也可以解决,但时间复杂度会高很多，因为多了很多不必要的计算，以1举例，则代码如下。

1. Windy数

def dfs(pos, pre_num, flag, lead):
    # 表示前一个数填的是pre_num,当前位pos可以填什么？其中flag表示前面所有是否贴着上限走，lead表示是否有前导0
    # lead表示是否有前导0 这个是需要的 如果最高位为0 其实搜索的是次高位以下的值(这就不像递推迭代法还需要分与nums同等数位和以下数位的，这个前导0就很奇妙，将这些情况容纳进来了。)
    # dfs终止条件
    global a    # 将上限数组引入进来
    if pos <= 0:
        # 如果搜索的数已经把最后一位数的值确定下来了 那么说明这个数有效 返回这个数的个数 也就是1
        return 1
    # 当前位数的确定
        # 提取当前位数所能取的最大数，如果前面都贴着上限走(即flag为True)则自然当前位也要贴着上限走
    max_num = a[pos] if flag else 9
    res = 0 # 统计当 前一个数为pre_num时 当前位所能填的Windy数的个数
    for i in range(max_num+1):
        if abs(pre_num - i) < 2:
            continue
        # 否则就是合理的 但是要注意是否有前导0 若有的话 则说明是次高位搜索 下一位可以随意 没有限制
        if lead and not i:
            # 如果前面为0并且当前也为0，则说明仍然前导为0，则下一位可以任取
            res += dfs(pos-1, -2, flag and (i==max_num), True)
        else:
            # 说明下一个数字填的不是首位了 此时有限制 按照常规走
            res += dfs(pos-1, i, flag and (i==max_num), False)
    return res

if __name__ == '__main__':
    N = 20  # 数字的最高位数
    nums = 4368
    a = [0] * N
    cnt = 0
    while nums:
        cnt += 1
        a[cnt] = nums%10
        nums//=10
    print(dfs(cnt, -2, True, True))

加上记忆化数位dp：

def dfs(pos, pre_num, flag, lead):
    # 表示前一个数填的是pre_num,当前位pos可以填什么？其中flag表示前面所有是否贴着上限走，lead表示是否有前导0
    # lead表示是否有前导0 这个是需要的 如果最高位为0 其实搜索的是次高位以下的值
    # dfs终止条件
    global a, dp
    if pos <= 0:
        # 如果搜索的数已经把最后一位数的值确定下来了 那么说明这个数有效 返回这个数的个数 也就是1
        return 1
    # 为避免重复计算，利用之前记录的状态
    # dp[pos][pre_num]表示前一个数为pre_num的当前数无限制(0-9)可填的满足条件的个数
    # 这里之所以填的是无限制可填的，是因为其用的更多这样记录更有效
    if not flag and dp[pos][pre_num] != -1:
        # 只要没有限制 被记录过就可以用
        return dp[pos][pre_num]
    # 当前位数的确定
        # 提取当前位数所能取的最大数
    max_num = a[pos] if flag else 9
    res = 0 # 统计当 前一个数为pre_num时 当前位所能填的Windy数的个数
    for i in range(max_num+1):
        if abs(pre_num - i) < 2:
            continue
        # 否则就是合理的 但是要注意是否有前导0 若有的话 则说明是次高位搜索 下一位可以随意 没有限制
        if lead and not i:
            # 如果前面为0并且当前也为0，则说明仍然前导为0，则下一位可以任取
            res += dfs(pos-1, -2, flag and (i==max_num), True)
        else:
            # 说明下一个数字填的不是首位了 此时有限制 按照常规走
            res += dfs(pos-1, i, flag and (i==max_num), False)
    if not flag and not lead:
        # 这里不可以记录前导0的，是因为有前导0的其pre_num为-2会把正确值覆盖掉
        # 这里若前导有0
        dp[pos][pre_num] = res
    return res

if __name__ == '__main__':
    N = 20 # 数字的最高位数
    nums =4368
    a = [0] * N
    cnt = 0
    while nums:
        cnt += 1
        a[cnt] = nums%10
        nums//=10
    dp = [[-1]*10 for _ in range(N)]
    print(dfs(cnt, -2, True, True))

2. tx笔试题：

def dfs(pos,num0,num1,flag,lead):
    # lead表示是否是前导0
    global upper_bound,dp
    # flag表示是否一直贴着前面选数
    if pos <= 0:
        return 1 if (num0 == num1) and (num0 !=0) else 0  # 满足条件的才计数,将0的情况排除掉 因为0不满足题意
    # 可以剪枝
    if not flag and dp[pos][num0][num1] != -1:
        # 只要为flag则当前位必定取到0-9，这个过程统计是重复的，因此可以记录下来，如果被记录过，则直接用就可以不用重复计算
        return dp[pos][num0][num1]
    # 为当前位置选上限 若前面都是贴着走 则上限自然为num对应的上限
    max_num = upper_bound[pos] if flag else 9
    res = 0 # 要求的是当前位所有满足条件的个数
    for i in range(max_num+1):
        # 可以从0开始，有前导0的当做小于cnt位的
        if lead and not i:
            res += dfs(pos-1, num0, num1, flag and (i==max_num),True)
        elif i%2 == 0:
            res += dfs(pos-1,num0+1,num1,flag and (i==max_num),False)
        else:
            res += dfs(pos-1,num0,num1+1,flag and (i==max_num),False)
    # 记录当前位时前面有num0个偶数，num1个奇数时所有满足条件的个数
    if not flag and not lead:
        dp[pos][num0][num1] = res
    return res

if __name__ == '__main__':
    num = 4368
    # 求0-num的数位上奇数与偶数个数相同的数字个数
    # 这里关心的是pos为止前面填了多少个奇数和偶数
    # dp[pos][num0][num1]前面填了num0个偶数，num1个奇数，当前位pos没有限制所能填数字个数 记忆化dp数组
    N = 20
    upper_bound = [0] * N  # 与上述的a数组同含义
    dp = [[[-1]*N for _ in range(N)] for _ in range(N)]  # 奇数和偶数个数不会超过位数
    cnt = 0
    while num:
        cnt += 1
        upper_bound[cnt] = num%10
        num//=10
    print(dfs(cnt, 0,0,True,True))