卡诺模板_卡诺地图（K-地图）

卡诺模板

In the previous articles, we have already discussed how we can use theorems of Boolean Algebra to simplify Boolean functions so that these simplified expressions help us in getting simple, less expensive and smaller circuits. Although, that method was helpful but also was difficult and non-systematic. We don't have any guarantee that we have reached a minimal expression. Thus, Karnaugh Maps (K-Maps) are used to simplify Boolean functions. K-Map is a systematic method to simplify Boolean expressions.

在先前的文章中，我们已经讨论了如何使用布尔代数定理来简化布尔函数，以便这些简化的表达式有助于我们获得简单，成本更低且更小的电路。 虽然，该方法很有用，但也很困难且不系统。 我们不能保证我们已达到最低要求。 因此， 卡诺地图(K-Maps)用于简化布尔函数。 K-Map是简化布尔表达式的系统方法。

卡诺地图(K-地图) (Karnaugh Map (K-Map))

A K-Map is a chart or graph composed of an arrangement of adjacent cells. Each of the cells represents one of the 2² possible products that can be formed from n-variables. Two different types of K-Map can be drawn for both CSOP and CPOS in terms of respective minterms and maxterms.

K-Map是由相邻单元格的排列组成的图表。 每个单元代表可由n变量形成的2 ²可能乘积之一 。 可以根据各自的最小项和最大项为CSOP和CPOS绘制两种不同类型的K-Map 。

1)2变量K-Map (1) 2-variable K-Map)

A 2-variable expression can have 2² = 4 possible ways of input representation. Thus, a 2-variable K-Map will have 4 adjacent cells representing each of the 4 possible combinations of inputs. Binary numbers at the top of the K-Map represent the condition of variable B along any column and binary number to the left of the K-Map represents the condition of variable A along any row.

2变量表达式可以具有2 ² = 4种可能的输入表示方式。 因此， 2变量K映射将具有4个相邻的像元，分别代表输入的4种可能组合中的每一种。 K-Map顶部的二进制数字表示沿任何列的变量B的条件，K-Map左侧的二进制数字表示沿任何行的变量A的条件。

Representation using minterms (SOP form):

使用minterm表示(SOP表格)：

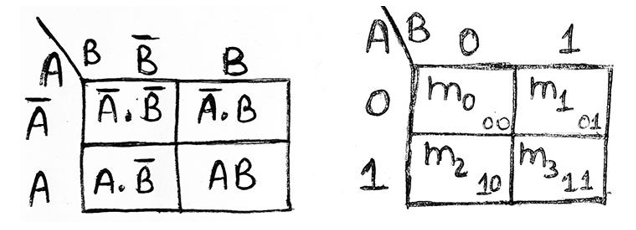
Representation using maxterms (POS form):

使用maxterms的表示形式(POS形式)：

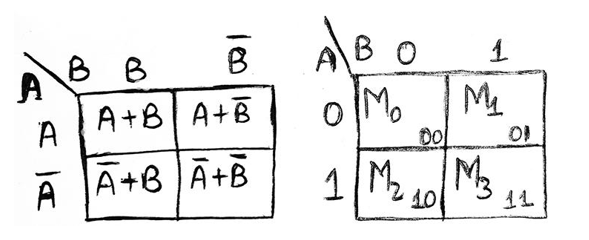
2)3变量K-Map (2) 3-variable K-Map)

A 3-variable expression can have 2³ = 8 possible ways of input representation. Thus, a 3-variable K-Map will have 8 adjacent cells representing each of the 8 possible combinations of inputs.

3变量表达式可以具有2 ³ = 8种可能的输入表示方式。 因此，一个三变量K-Map将具有8个相邻的像元，分别代表输入的8种可能组合中的每一种。

The thing to be noticed in the representation is that the binary numbers along the top of the K-Map are not in normal binary order. They are, in fact, in the Gray Code. This is to ensure that two physically adjacent squares are adjacent i.e., their minterms and maxterms differ by only one variable.

该表示法中要注意的是， K-Map顶部的二进制数字不是正常的二进制顺序。 实际上，它们在格雷码中。 这是为了确保两个物理上相邻的正方形相邻，即它们的最小项和最大项仅相差一个变量。

Representation using minterms (SOP form):

使用minterm表示(SOP表格)：

Representation using maxterms (POS form):

使用maxterms的表示形式(POS形式)：

3)4变量K图 (3) 4-variable K-Map)

A 4-variable expression can have 2⁴ = 16 possible ways of input representation. Thus, a 4-variable K-Map will have 16 adjacent cells representing each of the 16 possible combinations of inputs.

4变量表达式可以具有2 ⁴ = 16种可能的输入表示方式。 因此，一个4变量K映射将具有16个相邻的像元，分别代表输入的16种可能的组合中的每一种。

The binary number designations of the rows and columns are in Gray Code. Binary numbers at the top of the K-Map represents the condition of variables C and D along any column and binary numbers to the left of the K-Map represents the condition of variables A and B along any row.

行和列的二进制数字表示在格雷码中 。 K-Map顶部的二进制数字表示沿任何列的变量C和D的条件，K-Map左侧的二进制数字表示沿任何行的变量A和B的条件。

Representation using minterms (SOP form):

使用minterm表示(SOP表格)：

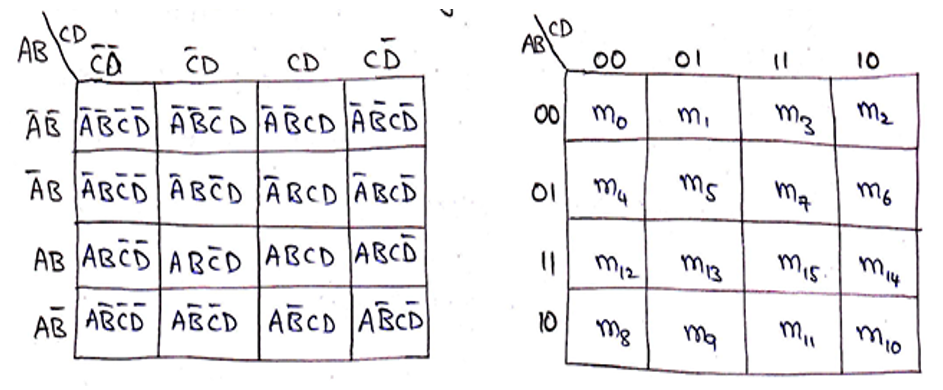
Representation using maxterms (POS form):

使用maxterms的表示形式(POS形式)：

翻译自: https://www.includehelp.com/basics/karnaugh-maps-k-maps.aspx

卡诺模板