Rivest-Shamir-Adleman（RSA）的密码学

The RSA algorithm is an asymmetric cryptography algorithm in cryptography. The Asymmetric eventually means that it implements two different keys i.e. Public Key and Private Key in cryptography. As like, the name tells that the Public Key is given to everyone and the Private key is kept private for others.

RSA算法是密码学中的一种非对称密码算法。 非对称最终意味着它实现了两个不同的密钥，即密码学中的公共密钥和私有密钥。 就像该名称一样，它告诉您将公钥提供给每个人，而私钥则对其他人保持私有。

As such a cryptosystem, the encryption key is public and it is different from the decryption key which is kept secret or as private. Mainly RSA, this is asymmetry is based on the practical high of the factorization of the multiple of two large prime numbers, the "factoring problem" in the cryptography. Then, the RSA is made of the first letters of the surnames of the publisher i.e. "Ron Rivest", "Adi Shamir" and "Leonard Adleman". It is published in 1977.

作为这样的密码系统，加密密钥是公共的，并且不同于保持秘密或私有的解密密钥。 主要是RSA ，这是不对称的，是基于两个大质数的倍数(在密码术中的“分解问题”)的分解的实用性高。 然后，RSA由发布者姓氏的首字母组成，即“ Ron Rivest”，“ Adi Shamir”和“ Leonard Adleman”。 它于1977年出版。

非对称密码的例子 (Example of asymmetric Cryptography)

1. A second party or client sends its public key to the server and requests for some data in cryptography.

   另一方或客户端将其公钥发送到服务器，并请求加密中的某些数据。

2. One more the server encrypts the data using the client's public key and sends the encrypted data to encrypt a key.

   服务器再使用客户端的公共密钥加密数据，然后发送加密的数据以加密密钥。

3. Second Party or Client receives this data and decrypts it.

   第二方或客户接收此数据并将其解密。

Hence, this is an asymmetric nobody else except client or second party can decrypt the data even if a third party has the public key of the client.

因此，这是不对称的，即使第三方具有客户端的公钥，除了客户端或第二方之外，其他任何人都不能解密数据。

RSA密钥对的生成 (Generation of RSA Key Pair)

Every person or a party who describes participating in communication using encryption needs to generate a pair of keys called namely public key and private key in the cryptography. The steps are followed in the generation of keys is described as following,

描述使用加密参与通信的每个人或一方都需要生成一对称为密码学的密钥，即公钥和私钥。 生成密钥的步骤如下，

• Find the RSA modulus (n)

  求出RSA模数(n)

  • Let two large primes, p and q.
  • Then, Calculate, n=p*q. For high encryption, let (n) be a large number, typically a minimum of 512 bits of the character.

• Now, Find Derived Number (e)

  现在，找到派生数(e)

  • Let, Number (e) must be between 1 and (p − 1)(q − 1).
  • Here, there will not be common factor for (e) and (p − 1)(q − 1) only 1. In other words two numbers e and (p – 1)(q – 1) are coprime for each other.

• Now, calculate the public key

  现在，计算公钥

  • The pair of public key numbers (n, e) form the RSA public key and is made public for everyone.
  • Therefore, though n is part of the public key, changes in factorizing a large prime number ensure that higher attackers cannot find in finite time the two primes (p and q) used to obtain n in this. This is the strength of RSA for cryptography.

• Now, generate the private key

  现在，生成私钥

  • Now, Private Key (d) is calculated from p, q, and e in this. For given n and e, there is unique number d for private or a key use by the author only.

• Here, number (d) is the inverse of e modulo (p - 1)(q – 1). This means that d is the number less than (p - 1)(q - 1) such that when multiplied by e, it is equal to 1 modulo (p - 1)(q - 1) in this cryptography.

  在此，数字(d)是e模(p-1)(q – 1)的倒数。 这意味着d是小于(p-1)(q-1)的数，因此当与e相乘时，它等于此密码术中的1模(p-1)(q-1)。

• This function is written mathematically as follows as e*d = 1 *mod (p − 1)(q − 1).

  该函数的数学写法如下：e * d = 1 * mod(p − 1)(q − 1)。

Example:

例：

Here, an example of generating RSA Key pair in cryptography is given below.

这里，下面给出在加密中生成RSA密钥对的示例。

• Let, two primes be p = 6 and q = 13. Then, n = p*q = 7 x 13 = 91.

  设两个素数为p = 6和q =13。然后，n = p * q = 7 x 13 = 91。

• Now, select e = 5, which is a valid since there is no number that is common factor of 5 and (p - 1)(q - 1) = 6 x 12 = 72, except for 1.

  现在，选择e = 5，这是有效的，因为除1之外，没有公因数为5且(p-1)(q-1)= 6 x 12 = 72的数字。

• Then, the pair of numbers (n, e) = (91, 5) forms the public key and can be made available to anyone which will be able to send us encrypted messages in the cryptography.

  然后，这对数字(n，e)=(91，5)构成了公共密钥，并且可以提供给任何能够以加密方式向我们发送加密消息的人。

    Input p = 7, q = 13, and e = 5 and find d=e^(-1)mod(p-1)(q-1)
    The output will be d = .29

• Now, check that the d calculated is correct or not:-d*e = 29 x 5 = 145 = 1 mod 72=1.

  现在，检查计算出的d是否正确：-d * e = 29 x 5 = 145 = 1 mod 72 = 1。

• Hence, public key is (n,e) i.e (91, 5) and private keys is(n,d) i.e (91, 29).

  因此，公钥是(n，e)，即(91，5)，私钥是(n，d)，即(91，29)。

• 加密与解密 (Encryption and Decryption)

  Hence, once the key pair of the private and public key has been generated, the process of encryption and decryption are relatively simple and easy to use by the keys.

  因此，一旦生成了私钥和公钥的密钥对，密钥的加密和解密过程就相对简单并且易于使用。

  Therefore, RSA does not directly operate on strings of bits as in case of symmetric key encryption in more opration. It operates on numbers as n. Here, it is necessary to represent the plaintext or original text as a series of numbers less than n in the RSA.

  因此，RSA不会像在对称密钥加密的情况下那样直接对位串进行操作。 它以数字n运算。 在此，有必要在RSA中将纯文本或原始文本表示为一系列小于n的数字。

  RSA加密 (RSA Encryption)

  • Now, Suppose the sender message to send some text message to someone whose public key is (n, e) in this.

    现在，假设发件人消息向其中的公钥为(n，e)的某人发送一些文本消息。

  • Then, the sender represents the plaintext as a series of numbers less than n in the process.

    然后，发送者在该过程中将纯文本表示为一系列小于n的数字。

  • Now, to encrypt the first plaintext P, which is a number modulo of n. The encryption process is simply done by a formula as C = P^e mod n

    现在，要加密第一个明文P，它是n的模数。 加密过程只需通过公式即可完成，即C = P ^ e mod n

  • In different words, the ciphertext C is equal to the plaintext P product by itself e times and then reduced modulo n in this. This means that C is also a number less than n in RSA.

    换句话说，密文C本身等于明文P乘积的e倍，然后以n为模降低。 这意味着在RSA中，C还要小于n。

  • Then, returning to our Key Generation example with plaintext as P = 10, we get ciphertext C: C = 10^5 mod 91=82

    然后，返回到以P = 10的明文的“密钥生成”示例，得到密文C：C = 10 ^ 5 mod 91 = 82

  RSA解密 (RSA Decryption)

  • Here, the decryption process for RSA is also very simple and easy. Suppose that the receiver of public-key pair (n, e) has received a ciphertext C as shown above.

    在这里，RSA的解密过程也非常简单。 假设公共密钥对(n，e)的接收者已经收到了密文C，如上所述。

  • Now, the receiver does the C to the power of his private key d. The result n will be the plaintext P as Plaintext = C^(d) mod n.

    现在，接收方将C发挥其私钥d的作用。 结果n将是纯文本P，因为Plaintext = C ^(d)mod n。

  • Now, returning to our example, the ciphertext as C = 82 would get decrypted to number to 10 using the private key as 29: Plaintext = 82^(29) mod 91 = 10

    现在，回到我们的示例，使用私钥作为29，将C = 82的密文解密为10：数字： Plaintext = 82 ^(29)mod 91 = 10

  
  
  
  

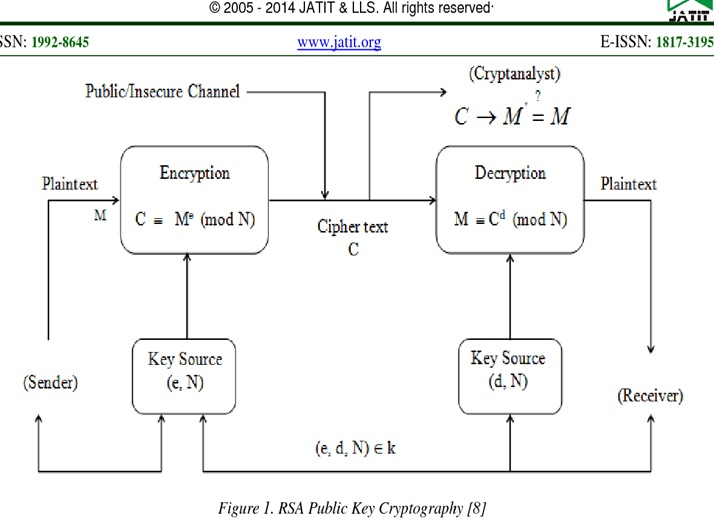
  Image source: https://www.semanticscholar.org/paper/Cryptanalytic-Attacks-on-Rivest%2C-Shamir%2C-and-(RSA)-Abubakar-Jabaka/209edc70b90515901adc08e1c5a27b90cb627421/figure/0

  图片来源：https://www.semanticscholar.org/paper/Cryptanalytic-Attacks-on-Rivest%2C-Shamir%2C-and-(RSA)-Abubakar-Jabaka/209edc70b90515901adc08e1c5a27b90cb627421/figure/0

  RSA分析 (RSA Analysis)

  The safety and security of RSA based on the strengths of two separate functions in it. Thus, the RSA cryptosystem is the most popular public-key cryptosystem in the cryptography strength of which is based on the practical high of factoring the very large numbers in this.

  RSA的安全性基于两个独立功能的优势。 因此，RSA密码系统是最流行的公钥密码系统，其密码强度是基于将其中的大量数字分解的实际高。

  • Encryption Function: This is considered as a single way function of transfer plaintext into ciphertext and it can be opposite only with the knowledge of private key d as private.

    加密功能：这被认为是将纯文本转换为密文的单向函数，并且只有在知道私钥d为私有的情况下才可以相反。

  • Key Generation: Mainly, the difficulty of determining a private key from an RSA public key is equivalent to factoring the n in RSA. A Hacker attacker thus cannot use knowledge of an RSA public key to determine an RSA private key unless he can factor n as n is large then he will not. It is also a single way function, going from p and q values to modulus n is easy but the reverse is not possible by these values only.

    密钥生成：主要而言，从RSA公共密钥确定私钥的难度等同于在RSA中分解n。 因此，黑客攻击者无法使用RSA公钥的知识来确定RSA私钥，除非他可以将n分解为n，否则n就不会。 它也是一个单向函数，从p和q值到模数n很容易，但仅通过这些值不可能相反。

  If one of these two functions is proved non-single-way, then RSA will be broken and the attacker can attack. Whereas, if a technique for factoring efficiently is developed then RSA will no longer be safe in the algorithm.

  如果证明这两个功能之一不是单向的，则RSA将被破坏，攻击者可以进行攻击。 而如果开发出一种有效分解因子的技术，则RSA在算法中将不再安全。

  The main strength or power of RSA encryption goes down against attacks if the number of p and q are not large primes or chosen public key e is a small number in this algorithm.

  如果p和q的数量不是大质数，或者选择的公共密钥e在此算法中很小，则RSA加密的主要强度或威力会遭到攻击。

  翻译自: https://www.includehelp.com/cryptography/rivest-shamir-adleman-rsa-in-cryptography.aspx