递推式子+矩阵快速幂+欧拉降幂

题目描述

百度之星2022年题——离散数学 题目链接

题目大致解析

• 大致解题思路
• 看到题目的n值如此之大，要么就是有结论，要么就是log级别的算法，而这种算方案数的一种最经典方式就是dp，dp中的log级别一般就是使用了矩阵快速幂加速。

递推式子

1. 寻找f[n]和f[n - 1]的直接关系（有时甚至还要考虑f[n - 2], f[n - 3]等）：得到0的情况很少，所以我们不妨先找到能够产生0的情况，再用总的选择数减去它即可。要使得n个数的情况能为0，则一个充分条件为【前n-1个数满足两个蕴含条件，且第n个数为0】，因为这样将导致第一个蕴含条件不满足；而事实上，这个条件也是一个必要条件，证明略过。
   $$f[n]=2^n-f[n-1]$$
2. 只有线性的式子才能被矩阵快速幂加速（因为要乘的矩阵的各元素均是常数），所以要进行转换，得到如下式子：
   $$f[n]=f[n-1]+2\ast f[n-2]$$
3. 右边有两类f，左边有一类f，不好设计矩阵，故增加如下的一个式子：
   $$f[n-1]=f[n-1]$$
4. 将上面两个式子用矩阵表示，如下所示, 矩阵递推步长为1：
   $$\left[\begin{array}{cc}f[n]& f[n-1]\end{array}\right]=\left[\begin{array}{cc}f[n-1]& f[n-2]\end{array}\right]\left[\begin{array}{cc}1& 1\\ 2& 0\end{array}\right]$$

欧拉降幂

• 相关公式如下，素数的欧拉函数为素数减一
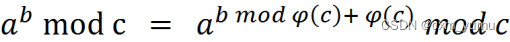
• 不太确定矩阵乘方是否能用欧拉降幂，暂时没有看到比较严格的证明，有大佬懂的话可以在评论区发一下，我这个做法也只是搬运别人的。

相关代码

• 个人认为本人的这个矩阵乘法和快速幂的板子还是蛮好用的

#include <iostream>
#include <stack>
#include <map>
#include <queue>
#include <string>
#include <vector>
#include <cmath>
#include <algorithm>
#include <string.h> 
using namespace std;
typedef long long ll;
#define int ll
const ll mod = 998244353;//不需要模的时候，把模数调大点即可 
typedef struct Mat{
    vector<vector<int>> m;
	int h, wide; 
    Mat(vector<vector<int>> &tmp){
    	m = tmp;
		h = m.size(), wide = m[0].size();
	};
	Mat(int h, int wide, int x = 0){
		m.resize(h);
		for (int i = 0; i < h; i++){
			m[i].resize(wide);
			for (int j = 0; j < wide; j++){
				m[i][j] = x;
			}
		}
		this -> h = h, this -> wide = wide;
	};
}Mat;//存储结构体
Mat mat_mul(Mat x,Mat y)
{
    Mat c(x.h, y.wide);
    for(int i = 0; i < x.h; ++i){
        for(int j = 0; j < y.wide; ++j){
            for(int k = 0; k < y.h; ++k){
                c.m[i][j] = (c.m[i][j] + x.m[i][k] * y.m[k][j] % mod) % mod;//可选择更换为其他的求矩阵元素的操作 
            }
        }
    }
    return c;
}
Mat mat_pow(Mat x, ll y)//矩阵快速幂
{
    Mat ans(x.h, x.h);
    for (int i = 0; i < ans.h; i++){//要初始化为1矩阵，注意不是全1！ 
    	ans.m[i][i] = 1;
	}
    while(y){
        if(y & 1) ans = mat_mul(ans, x);
        x = mat_mul(x, x);
        y >>= 1;
    }
    return ans;
}
vector<vector<int>> a = {{1, 1}, {2, 0}};//一些初始矩阵可以这样初始化
vector<vector<int>> f = {{3, 1}};
void solve(){
    string s;
    cin >> s;
    int n = 0;
    for(int i = 0 ; s[i] ; i ++ )
        n = (n * 10 + s[i] - '0') % (mod - 1);
    n = (n - 2 + mod - 1) % (mod - 1);
    Mat a_mat(a);
	Mat f_mat(f);
	Mat ans(mat_mul(f, mat_pow(a, n)));
	cout << ans.m[0][0] << endl;
}

signed main(){
	std::ios::sync_with_stdio(false);
	std::cin.tie(0); 
	std::cout.tie(0);
	int T = 1;
	while(T--){
		solve();
	}
	return 0;
}