二叉树的销毁（O(1)空间复杂度）

本文主要介绍二叉树的删除。
一、递归
算法思想：
在释放某节点时，该节点的左、右子树都已经释放，所以，应该采用后序遍历。

二、非递归
同时要求：不能使用栈，空间复杂度必须为O(1)
算法思想：借助链栈，同时把每个节点的左指针（lchild）看成是链栈中的next指针，然后将后序遍历中需要压入栈的节点原地连成一个链式栈。

补充：链式栈简介
（1）栈的链接存储结构称为链栈。
（2）通常链栈用单链表表示，因此其节点结构与单链表的节点结构相同。因为只能在栈顶执行插入和删除操作，显然以单链表的头部作栈顶是最方便的，而且没有必要像单链表那样为了运算方便附加一个头节点。
（3）空栈时，由于链栈不带头节点，因此只需将栈顶指针top置为空。
（4）入栈和出栈：链栈的插入操作和删除操作只需要处理栈顶即第一个位置的情况，而无需考虑其他位置的情况。
（5）取栈顶元素：只需返回栈顶指针top所指节点的数据域。
（6）判空操作：只需判断top = NULL是否成立，若成立，则栈为空。

具体实现如下：

#include <iostream>
using namespace std;

typedef struct node
{
    char data;
    struct node *lchild;
    struct node *rchild;
}BiNode, *BiTree;


// 先序建立二叉树 （输入时，按先序次序输入二叉树中结点的值,以 # 字符表示空树）
BiTree createBiTree()
{
    BiTree T;

    char c;
    scanf("%c", &c);

    if (c == '#')
        T = NULL;
    else
    {
        T = new BiNode;  // 或 T = (BiTree)malloc(sizeof(BiNode));
        T->data = c;

        T->lchild = createBiTree();
        T->rchild = createBiTree();
    }

    return T;

}


// 二叉树的销毁（递归）
void releaseTree2(BiTree &T)  // 此处的参数使用引用形式，仅是为了防止出现打印异常。
{
    if (T != NULL)
    {
        releaseTree2(T->lchild);
        releaseTree2(T->rchild);
        delete T;
        T = NULL;

    }
}


// 二叉树的销毁（非递归＋O(1)空间复杂度）
void releaseTree(BiTree &root) // 此处的参数使用引用形式，仅是为了防止出现打印异常。
{
    BiTree top = NULL; // 链式栈的栈顶（此时为NULL，即空栈）
    BiTree temp, q;

    temp = root->lchild; // 先将二叉树根节点的左孩子保存在temp变量中
    root->lchild = top; // 此处的lchild相当于单链表中的next，所以此处是让根节点入链式栈，栈底元素为NULL；注意链式栈和顺序栈的区别。
    top = root; // 链式栈的栈顶此时为root

    while(top != NULL)
    {
        while(temp != NULL) // 通过循环，将根节点的左子树(还有左子树的左子树，...)的根节点，加入链式栈
        {
            q = temp;
            temp = q->lchild; // 始终用temp来保存当前子树根节点的左孩子
            q->lchild = top; // 当前子树的根节点入链式栈
            top = q; // 链式栈的栈顶此时为q
        }
        temp = top; // 此时的temp对应的栈顶top，是整棵树的最左子树的根节点
        if(temp->rchild != NULL)
        {
            q = temp;
            temp = q->rchild; // 将当前栈顶节点的右子树非空，则将该右子树保存到temp变量中，在下一次循环时，再次进入到while(temp != NULL)，然后将该子树的左子树(还有左子树的左子树，...)的根节点，加入链式栈。
            q->rchild = NULL;  // 此时已经使用过当前栈顶节点的rchild来访问，不会再次使用，故清空。
        }
        else
        {
            top = temp->lchild; // 若当前栈顶节点的右子树为空，则当前栈顶节点出链式栈。出栈前，先改变栈顶指针。
            free(temp); // 释放当前栈顶节点
            temp = NULL; // 指针清空
        }
    }

    root = NULL; // 最后清空根节点指针
}


// 前序遍历
void PreOrderTraverse(BiTree T)
{
    if (T)
    {
        printf("%c\n", T->data);
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);

    }
}

int main(int argc, const char * argv[]) {

    BiTree T = createBiTree(); // 建立

    PreOrderTraverse(T);

    printf("---------------------\n");

    releaseTree(T); // 非递归
    PreOrderTraverse(T);


//    releaseTree2(T); // 递归
//    PreOrderTraverse(T);
//   // 销毁后，再执行打印时，应该打印为空，但是可能会打印出一些其他数据(如a)，why？
//   // 原因：此处销毁二叉树时，传入的二叉树的根节点(T)是值传递，即使在销毁的过程中对T做了清空操作(T = NULL)也没用，仍然有可能会打印出其他数据。
//   // 解决方案：直接传递引用即可，例如，把releaseTree2函数的参数改为引用形式，void releaseTree2(BiTree &T)。

    return 0;
}

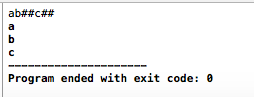
输入输出示例如下：