Jazz_Charles的Dog数列
Description
Jazz_Charles发现了一个数列称为Dog数列:
A[1] = 1
A[2] = 1
A[n] = A[n-1] + 8*A[n-2]
onisac看到这个数列之后,问了Jazz_Charles一个简单的问题,给定一个整数n,求A[n]是多少?
Jazz_Charles自然是答不来的,所以他请你替他回答这个问题。
(Dog数列名称由来(●'◡'●))
Input
多组数据,每组一行,一个整数n(0<n<=10000000000000)
Output
每组输出一行,输出A[n] (对100000007取膜)
Sample Input
1 2 3
Sample Output
1 1 9
HINT
暴力写是不行的哦
汪汪汪 java BigInteger BigDecimal花式TLE
换C++大数模板花式TLE
搜OEIS看到通项公式 a(n) = (((1+sqrt(33))/2)^(n+1) - ((1-sqrt(33))/2)^(n+1))/sqrt(33).
然后心里美滋滋的暴力一发花式TLE
然后灵光一闪 这不是和快速幂模很像吗。。
果然自己还是太弱了。。这摆明了要0(logn)的算法,我用O(n)硬怼。。
但小数又没有取模规则。。肯定有其他方法。。
然后到处找找到了做法。。
随缘写了一发过了。。
题解:用矩阵快速幂
这很重要,上面的是用矩阵快速幂来模拟斐波那契数列的过程
详情百度搜索poj3070or斐波那契数列快速幂模
所以这道题的单位矩阵变一下就好了,变成:1,1
8,0
也就是说(b,a)*(1,1) =(b+8*a,b);(意思理解就好了)
(8,0)
看
也就是说乘一次转换矩阵就相当变换了一次,而原始矩阵我们可以构造的和转换矩阵一样,因为恰好F(1)=1且F(2)=1,见图,左是原始矩阵(正好跟转换矩阵一样),右是我们每次乘的矩阵。
//算了我编不下去了,其实是随便猜了一个正好对了就是这样。。(划掉)
而快速幂的好处就是将本来一个一个乘导致的O(n)的复杂度降到O(logn)所以不会超时,而因为取模规则a^n%p可以化简为((a%p)^n)%p/*(大概0.0,记得是这样的。。)*/所以每次取模保证不会溢出,快速幂中也可以运用这条规则,这就造就了快速幂模完美地解决了时间复杂度和溢出的问题。
AC Code:
//package K;
import java.io.*;
import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.*;
public class Main {
static final long MOD=100000007;
static Matrix ans=new Matrix();
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
while(sc.hasNext()){
long cur=sc.nextLong();
if(cur==1||cur==2)
System.out.println(1);
else{
Matrix base =new Matrix(1,1,8,0);
System.out.println(matrix_pow(base,cur));
}
}
}
static Matrix multi(Matrix a, Matrix b) {
Matrix tmp=new Matrix();
for(int i = 0; i < 2; i++) {
for(int j = 0; j < 2; j++) {
tmp.m[i][j] = 0;
for(int k = 0; k < 2; k++)
tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;
}
}
return tmp;
}
static long matrix_pow(Matrix a, long n) {
ans.m[0][0] = ans.m[1][1] = 1;
ans.m[0][1] = ans.m[1][0] = 0;
while(n!=0) {
if((n & 1)!=0) ans = multi(ans, a);
a = multi(a, a);
n >>= 1;
}
return ans.m[0][1];
}
}
class Matrix{
long[][] m;
Matrix(){
this.m=new long[2][2];
}
Matrix(long a,long b,long c,long d){
this.m=new long[2][2];
this.m[0][0]=a;
this.m[0][1]=b;
this.m[1][0]=c;
this.m[1][1]=d;
}
}
算了再来发C++:
#include <cstdio>
#include <cstring>
#include <cmath>
#include<iostream>
using namespace std;
const long long MOD = 100000007;
struct matrix {
long long m[2][2];
}ans;
matrix base = {1, 1, 8, 0};
matrix multi(matrix a, matrix b) {
matrix tmp;
for(int i = 0; i < 2; i++) {
for(int j = 0; j < 2; j++) {
tmp.m[i][j] = 0;
for(int k = 0; k < 2; k++)
tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;
}
}
return tmp;
}
long long matrix_pow(matrix a, long long n) {
ans.m[0][0] = ans.m[1][1] = 1;
ans.m[0][1] = ans.m[1][0] = 0;
while(n) {
if(n & 1) ans = multi(ans, a);
a = multi(a, a);
n >>= 1;
}
return ans.m[0][1];
}
int main() {
long long n;
while(cin>>n) {
printf("%lld\n", matrix_pow(base, n));
}
return 0;
}







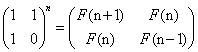

















 851
851

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








