《中国古代数学思想》读书笔记（15）

　

《中国古代数学思想》读书笔记（15）
　　 　作者：中科大胡不归
　　

　 第四章：数学思想的理论奠基——刘徽的数学思想。本篇记录此章第3节的第3部分和第4节的第1、2、3部分。

4.3 极限（无限）思想——前无古人的算法

3、开方不尽数

　　这是在《九章算术》少广章开方术的注文中提出的，也是数学史上非常有名的话题：
　　“术文：若开之不尽者，为不可开，当以面命之。

注文：术或有以借算加定法而命分者，虽粗相近，不可用也。凡开积为方，方之自乘当还复有积分。令不加借算而命分，则常微少；其加借算而命分，则又微多。其数不可得而定。故惟以面命之，为不失耳。譬犹以三除十，以其余为三分之一，而复其数可以举。不以面命之，加定法如前，求其微数。微数无名者以为分子，其一退以十为母，其再退以百为母。退之弥下，其分弥细，则朱幂虽有所弃之数，不足言之也。

　　术文：若实有分者，通分内子为定实，乃开之。讫，开其母，报除。若母不可开者，又以母乘定实，乃开之。讫，令如母而一。”
　　开方术的原文肯定了开方不尽数的存在，把sqrt (N)称为N的“面”，即平方根，不论N是不是完全平方数。这是一个了不得的数学认识，离无理数的发现也就是一步之差了！按：但这一步之差中国古人就是没跨过去呀。毕达哥拉斯学派早在刘徽之前几百年就发现了sqrt (2)是无理数，跨过了这一步之差。
刘徽指出“以借算加定法而命分”。设N开方已得的根为a，则有

sqrt(N)≈a+(N−a2)/(2a+1)

$$sqrt (N) ≈ a + (N - a^2) /(2a + 1)$$ ，
　　还有不加借算而给出的结果
　 $$sqrt (N) ≈ a + (N - a^2) /2a$$ 。
　　非常重要的是刘徽指出
　 $$a + (N - a^2) /(2a + 1) < sqrt (N) < a + (N - a^2)/2a$$ ，
　　　得出了从不足近似值和过剩近似值两方面逼近方根的认识和方法，在世界上是处于先进行列的。按：在刘之前，阿基米德得到了同样的不足近似值和过剩近似值。他求出了根号3的很好的近似值：1351 /780 > sqrt(3) > 265 /153。
　　更重要的是，刘徽提出了不用分数逼近方根，而按前面的方法，不断退位，一直用开方术计算下去，得到“微数”，就是十分小的数，而且是十进小数。因此这里是给出的是用十进小数逼近方根，开启了用小数逼近无理数的先河，真正是具有世界历史意义的成果。按：这话有可疑之处。用小数逼近是没错，但无理数的概念，刘徽根本没想到。
　　开方术的最后两句话给出了分数开方的算法：
设A是完全平方数，则
　 $$sqrt (C + B /A) = sqrt [(CA + B) /A] = sqrt (CA + B) /sqrt (A)$$ ，
设D不是完全平方数，则
$$sqrt (E /D) = sqrt (ED /D2) = sqrt (ED) /D$$ 。
　　这也是与现代十分一致的结果。按：本书没有说清楚，这是《九章算术》原文的内容，不是刘徽的新结果。此外，如果要开方的数不能表示成有限分数，怎么办？这说明他们只考虑了有理数的开方，完全没考虑无理数的开方。中国古人离无理数的概念不是一步之遥，而是离得远呢！

4.4 以盈补虚思想——出入相补的原理

　　以盈补虚是刘徽进行算法解释或者说进行证明的一种基本思想。从这种思想出发，刘徽提出了一个基本原理——出入相补原理。最典型的就是在圆田术、开方术和各种“化圆为方”问题中的应用。
1、初次应用

　　刘徽第一次应用出入相补原理，是在方田章中为圭田术作的注文中。按：圭是古代帝王、诸侯举行隆重仪式所执玉制礼器，上尖下方。圭田即三角形田。
　　“又有圭田广五步二分步之一，从八步三分步之二，问为田几何？
　　答曰：二十三步六分步之五。
　　术曰：半广以乘正从。
　　注文：半广知，以盈补虚为直田也。亦可半正从以乘广。按半广乘从，以取中平之数，故广从相乘为积步。亩法除之，即得也。”

译文：用广（底边）的一半乘从（高）。取广的一半，是为了以盈补虚，使它变为长方形田。又可以取从的一半乘广。

　　术中所说的方法可以图示出来。

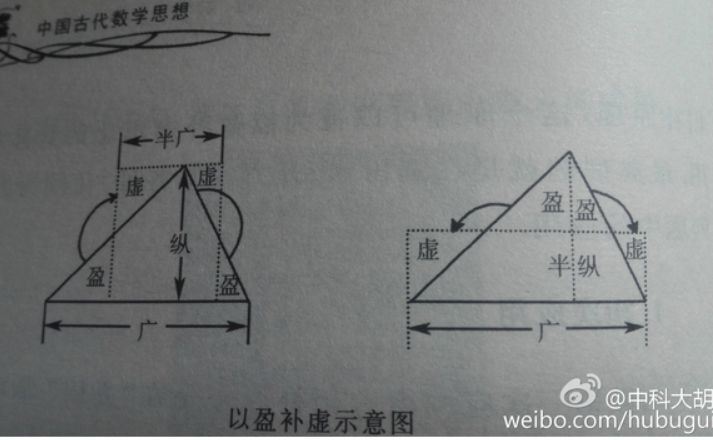
　　出入相补原理在方田章下文的邪田（直角梯形）、箕田（梯形）以至于圆田等几乎所有的求积计算中得到应用。
　　出入相补的做法本质上都是把面临的问题转化为已经解决的问题——就是现在所说的“关系映射反演”方法，这是现代数学中最基本最重要的数学思想或者数学方法。

2、在“圆田术”注中的运用
　　“术曰：半周半径相乘得积步。
　　注文：按：半周为从，半径为广，故广从相乘为积步也。假令圆径二尺，圆中容六觚之一面，与圆径之半，其数均等。合径率一而外周率三也。”

译文：把半周作为从，半径作为广，按照方田术广从相乘即得到积步。假设圆的直径是2尺，那么圆内接正六边形的一边，与圆的半径，在数值上是相等的。这符合前人圆周长是直径三倍的认识。

　　这是刘徽指出前人之说，并用出入相补原理推证。将圆内接正六边形的周长作为圆周长，正12变形的面积作为圆面积。如下图，形成一个以圆半径为广、正六边形周长的一半为从的长方形。这是对出入相补原理的进一步应用。

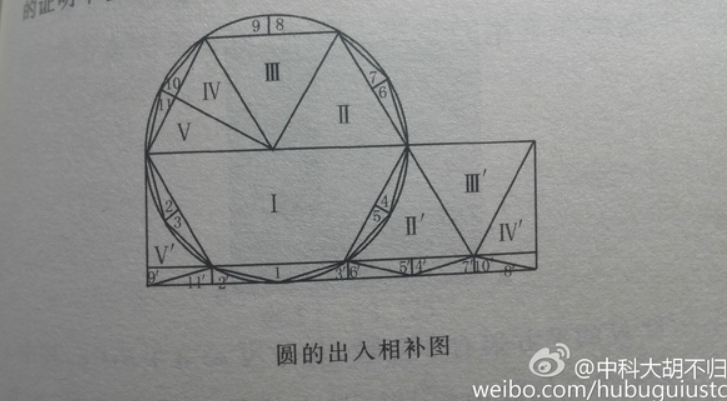
3、开方术解释

　　刘徽对少广章开方术的注解是出入相补原理的一个出色的运用，得到了非常现代的数学结果。
　　“开方。注文：求方幂之一面也。
　　术曰：置积为实。借一算，步之，超一等。
　　注文：言百之面十也。言万之面百也。
　　术文：议所得，以一乘所借一算为法，而以除。
　　注文：先得黄甲之面，上下相命，是自乘而除也。
　　术文：除已，倍法为定法。
　　注文：倍之者，豫张两面朱幂定袤，以待复除，故曰定法。
　　术文：其复除，折法而下。
　　注文：欲除朱幂者，本当副置所得成方，倍之为定法，以折、议、乘，而以除。如是当复步之而止，乃得相命。故使就上折下。
　　术文：复置借算，步之如初。以复议一乘之。
　　注文：欲除朱幂之角黄乙之幂，其意如初之所得也。
　　术文：所得副以加定法，以除。以所得副从定法。
　　注文：再以黄乙之面加定法者，是则张两青幂之袤。
　　术文：复除，折下如前。”
　　用图来解释刘徽的注文。

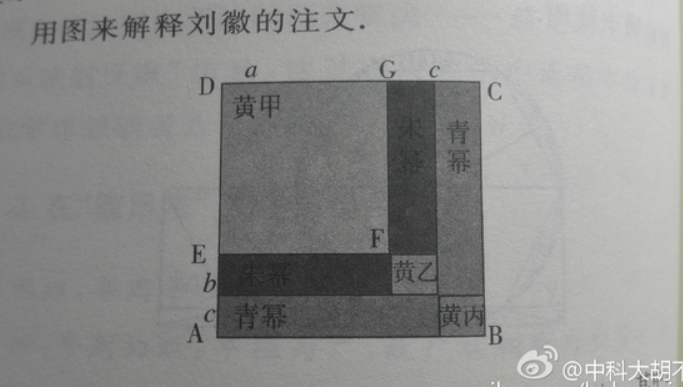
　　设N的平方根有三位数，$sqrt (N) = a + b + c$，其中$a = 100a_1$是百位数，$b =10b_1$是十位数，c是个位数。N是正方形ABCD的面积。
　　开方时，先估计根的百位数a，就是“先得黄甲之面，上下相命，是自乘而除也”，从N中减去$a^2$（黄甲），剩下曲尺形EABCGF。
　　再求十位数b，从曲尺形中减去$2ab + b^2$。就是减去两个朱幂，以及黄乙。
再求个位数c，从曲尺形中减去$2 (a + b)c + c^2$，就是两个青幂和黄丙。正好减尽。如位数不止3位，可以按上述继续做下去。
　　开方术的这个算法，与现代笔算的开平方法完全一致。