SVM算法

自从开始工作了以后，就很少有时间去接触原先熟悉的那些机器学习算法，前段时间一个同学询问关于svm算法的事情，突然发现原来能够熟练推导的东西，现在也很生疏了，最近正在读周志华老师的《机器学习》，借此机会，尽量把常见的机器学习算法总结一下。

SVM算法基本型

首先，以一个二类的问题开始，我们假设样本数据集是$D=\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}),\cdots ,(x^{(m)}, y^{(m)}) \}$，其中$y^{(i)}\in\{-1,+1\}$。对于分类问题来说，就是寻找一个最佳的超平面将训练数据集划分为几部分。对于上面这个二类问题来说，总是有很多超平面将训练集划分，如下图所示

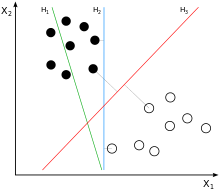
图中，蓝色的线跟红色的线都能准确的将训练数据集划分，但是从直观的角度，我们会认为红色的线更好，因为红色的线距离两类样本的距离都是比较远的，这样当有新的数据进行分类的时候，红线允许的数据扰动会更大，换句话说，红线的鲁棒性更好一点。

那么从几何的角度来看，分类的超平面可以通过如下的线性方程来表:示

$$\begin{equation} w^{T}x+b=0 \tag{1} \end{equation}$$
其中， $w=\{w_1,w_2,\cdots,w_d\}$表示超平面的法向量， $b$表示的是超平面与原点之间的距离。而点到超平面的距离可以通过下面表达式求得：
$$\begin{equation} \frac{|w^{T}x+b|}{||w||} \tag{2} \end{equation}$$

SVM算法就是要找到最佳的超平面，即希望能够找到这样的$w$和$b$，能够使得

$$\begin{equation} w^{T}x+b^{(i)}\geq+1, y^{(i)}=+1\\ w^{T}x+b^{(i)}\leq-1, y^{(i)}=-1 \tag{3} \end{equation}$$
上面两个式子可以改写为
$$\begin{equation} y^{(i)}(w^{T}x+b^{(i)})\geq+1 \tag{4} \end{equation}$$
可以注意到，在这里，不是像传统的分类问题，要求 $y^{(i)}(w^{T}x+b^{(i)})>0$，这是因为为了能够得到更好的泛化能力，为了不仅仅是希望训练的实例在分类超平面的两侧，还希望实例能够到超平面具有一定的距离。在训练数据中，距离超平面最近的几个点可以使等式成立，我们将那几个点称为“支持向量”。

在这里，支持向量到超平面的距离称作边缘(margin)，通过公式(2)(4)可以知道超平面到两侧的边缘为$\frac{2}{||w||}$，我们要求的最佳超平面即是最大化边缘的超平面，即满足

$$\begin{equation} \max \frac{2}{||w||}\\ s.t.\text { }y^i(w^Tx+b)\geq1, i=1,2,\cdots,m \tag{5} \end{equation}$$
可以知道，公式(5)可以转换为：
$$\begin{equation} \min \frac{1}{2}||w^2||\\ s.t.\text { }y^i(w^Tx+b)\geq1, i=1,2,\cdots,m \tag{6} \end{equation}$$

对偶问题

下面开始求解公式(6)，可以看出公式(6)是一个凸二次规划的问题，可以通过很多现有的优化方法进行优化，但是通过其对偶问题进行求解更为简单高效。

对公式(6)使用拉格朗日乘子法，即：

$$\begin{equation} L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_{i}(1-y^{(i)}(w^Tx^{(i)}+b)) \tag{7} \end{equation}$$
其中， $\alpha=\{\alpha_{1},\alpha_{2},\cdots,\alpha_{m}\}, \alpha_{i}\geq0$
首先，需要明确的一点是公式(7)关于 $\alpha^{i}$求最大等价于公式(6)中的目标函数，即
$$\begin{equation} \frac{1}{2}||w||^2=\max_{\alpha:\alpha_{i}\geq0}L(w,b,\alpha) \tag{8} \end{equation}$$
简单证明一下上式：当