C语言数据结构笔记——一次搞定十大排序算法

已于 2023-04-24 15:01:17 修改
阅读量370 收藏 7
点赞数
分类专栏： C++ 学习笔记 文章标签： 数据结构 算法 c++
于 2021-09-20 19:59:47 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/daimashiren/article/details/120205776
版权

准备工作

定义一个基础的交换函数swapValue()和打印函数output()以便于后续排序函数的调用。

#include<iostream>
#include<Windows.h>
using namespace std;

void swapValue(int &a , int &b);
void output(int arr[], int len);


void swapValue(int &a , int &b)
{
    int temp = a;
    a = b;
    b = temp;
}


void output(int arr[],int len)
{
    int i;
    for (i = 0; i < len; i++)
        cout<<arr[i]<<" ";
    cout<<endl;
    Sleep(1000);
}

 一.冒泡排序

算法核心：每次从前往后扫描，两两交换值，较大值依次沉底，执行n-1趟之后即可完成排序。

时间复杂度：O(n^{2})

空间复杂度：O(1)

稳定性：稳定

适用情况：n较小，初始序列基本有序

void bubbleSort(int arr[],int len)
{
    int i,j;
    for(i = 0; i < len-1; i++)    
        for(j = 0; j < len-1-i; j++)
            if(arr[j] > arr[j+1])
            {
                swapValue(arr[j], arr[j+1]);
            }
}

实例测试——冒泡排序

int main() {
    int arr[] = {23,54,66,12,7,89,45,33,97,30};
    int len = (int) sizeof(arr) / sizeof(*arr);
    bubbleSort(arr, len);
    return 0;
}

 注意观察序列末尾，较大的值依次沉底。

二.简单选择排序

算法核心：依次从未排序的序列中选择出最小的值放到已排序的序列末尾，重复n-1趟后即可完成排序。

时间复杂度：O(n^{2})

空间复杂度：O(1)

稳定性：不稳定

适用情况：n较小

void selection_sort(int arr[],int len)
{
    int i,j,temp;
    for(i = 0; i < len-1; i++)
    {
        int min =i;
        for(j = i + 1; j < len; j++)
            if(arr[j] < arr[min])
            {
                min = j;     //找到未排序序列中最小值的下标
            }
        if(min != i)
        {
            swapValue(arr[min], arr[i]);
            output(arr, len);
        }
    }
}

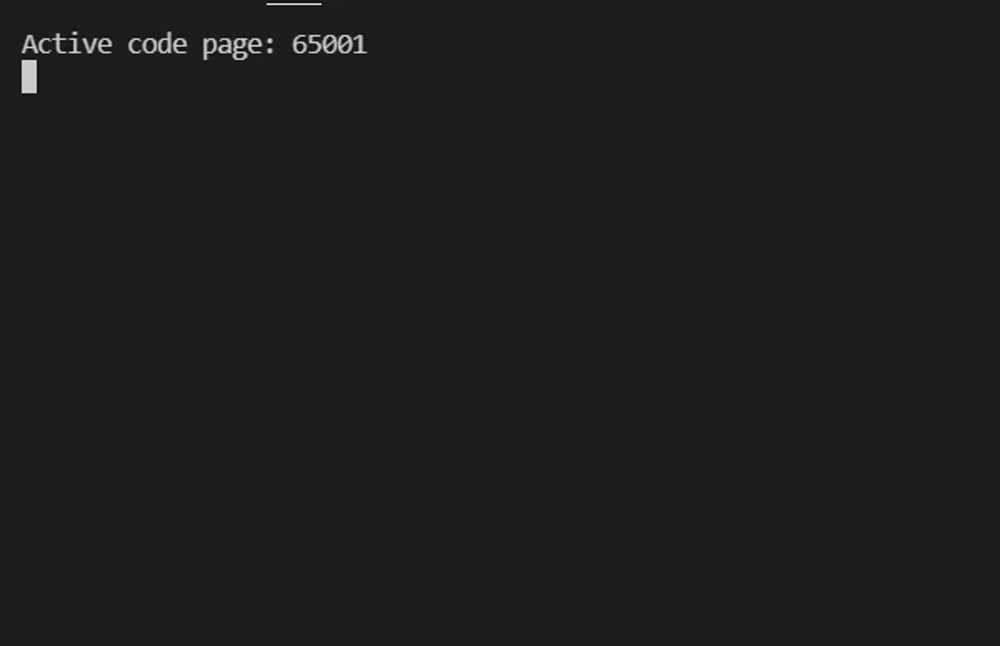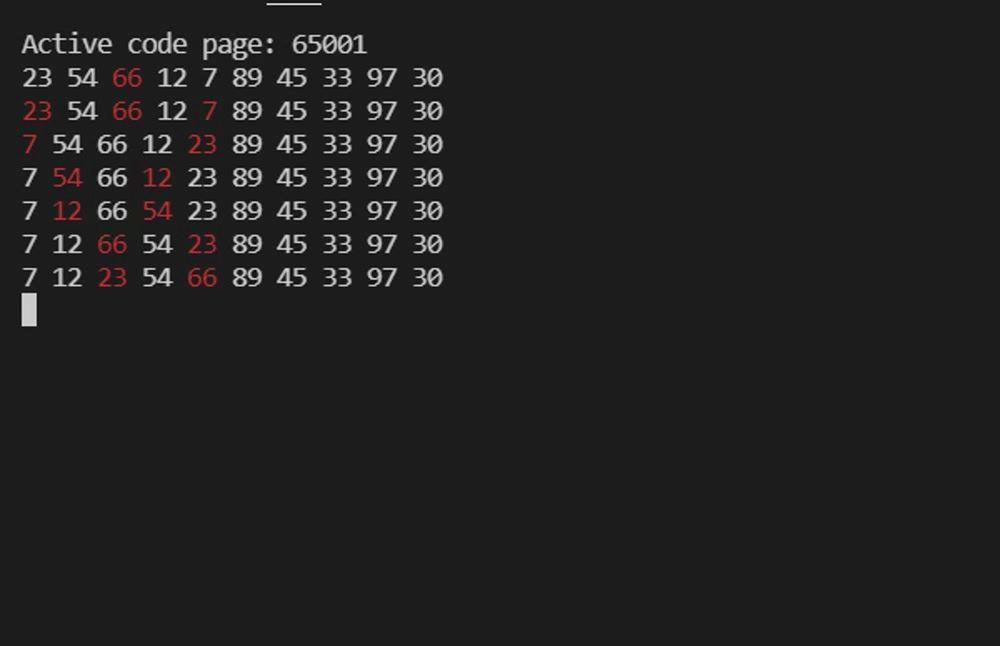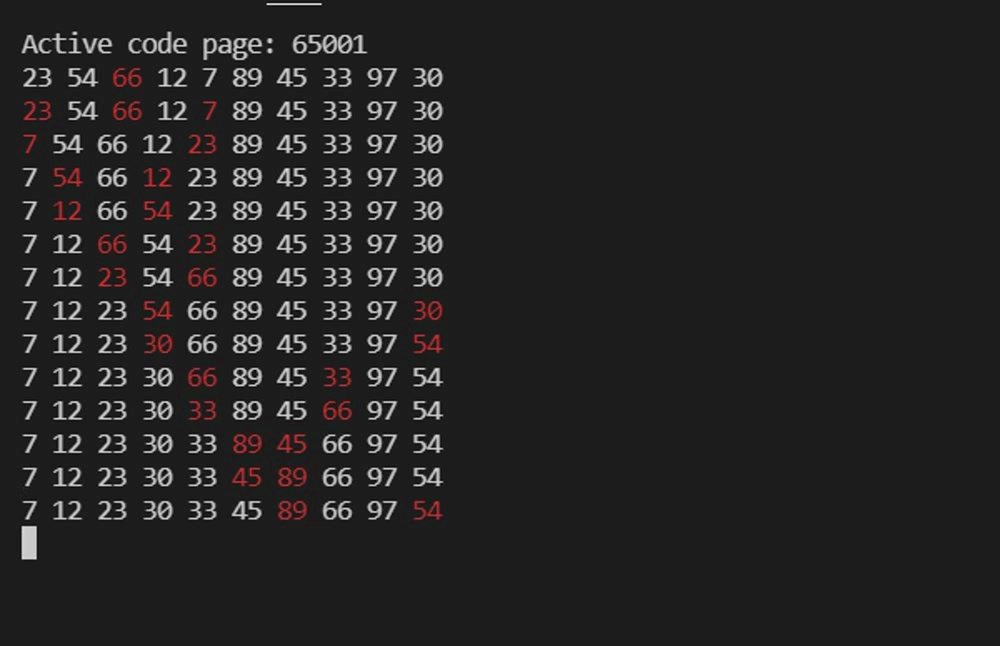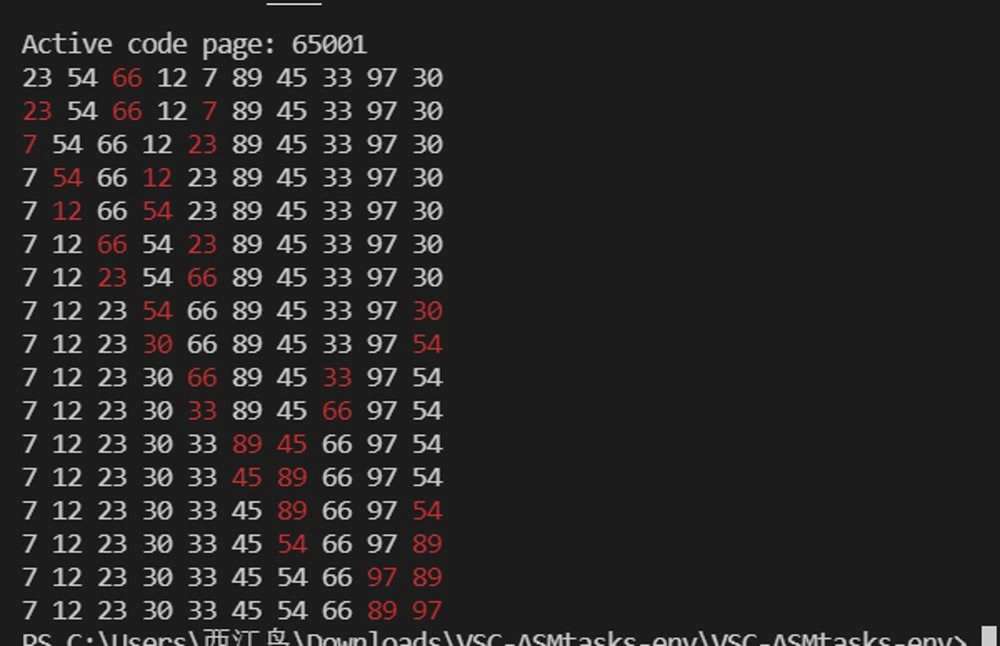
实例测试——简单选择排序 

int main() {
    int arr[] = {23,54,66,12,7,89,45,33,97,30};
    int len = (int) sizeof(arr) / sizeof(*arr);
    selection_sort(arr, len);
    int i;
    return 0;
}

 注意观察序列前部，未排序序列中的最小值被依次前置。

 三.直接插入排序

 算法核心：将未排序序列中的元素依次插入到已排序的序列中，找到合适的插入位置后需要依次后移元素，给新插入的元素腾出地方。

时间复杂度：O(n^{2})

空间复杂度：O(1)

稳定性：稳定

适用情况：n较小，初始序列基本有序

void insertion_sort(int arr[],int len)
{   
    int i,j,temp;
    for(i = 1; i < len; i++)
        {
            temp = arr[i];
        for(j = i; j > 0 && arr[j-1] > temp; j--)
            {
                arr[j] = arr[j-1];      //插入的位置后的元素依次后移
            }
        
        arr[j] = temp;      
        /*每次循环结束，j--,此时的arr[j]已经向后复制到了arr[j+1]处，即arr[j]=arr[j+1]
        并且此时arr[j-1]<=temp,因此可放心将temp插入到arr[j]处
        */
        }
}

实例测试——直接插入排序

int main() {
    int arr[] = {23,54,66,12,7,89,45,33,97,30};
    int len = (int) sizeof(arr) / sizeof(*arr);
    output(arr,len);
    insertion_sort(arr, len);
    return 0;
}

 注意观察插入的位置后的元素依次向后移动的过程。

四.希尔排序(改进的插入排序)

算法核心：直接插入排序对基本有序的序列排序效率较高，因此可以通过设置一个增量gap，以间隔为gap的数作为一组，在其内部进行插入排序，依次减少增量gap并重复上述步骤，直到gap=1时，希尔排序退化为直接插入排序。

时间复杂度：O(n^{1.3})

空间复杂度：O(1)

稳定性：不稳定

void shell_sort(int arr[],int len){
    int gap,i,j;
    int temp;
    for(gap = len>>1; gap > 0; gap = gap>>1)    //增量gap每次减小一半
        {
            for(i = gap; i < len; i++)        //组内进行直接插入排序
            {
                temp = arr[i];
                for(j = i-gap; j >= 0 && arr[j] > temp; j -= gap)
                {
                    arr[j+gap] = arr[j];  //组内元素依次后移

                }
                arr[j+gap] = temp;        //插入元素,此时arr[j+gap]位置元素已经备份至arr[j+2*gap]处
            }
        }

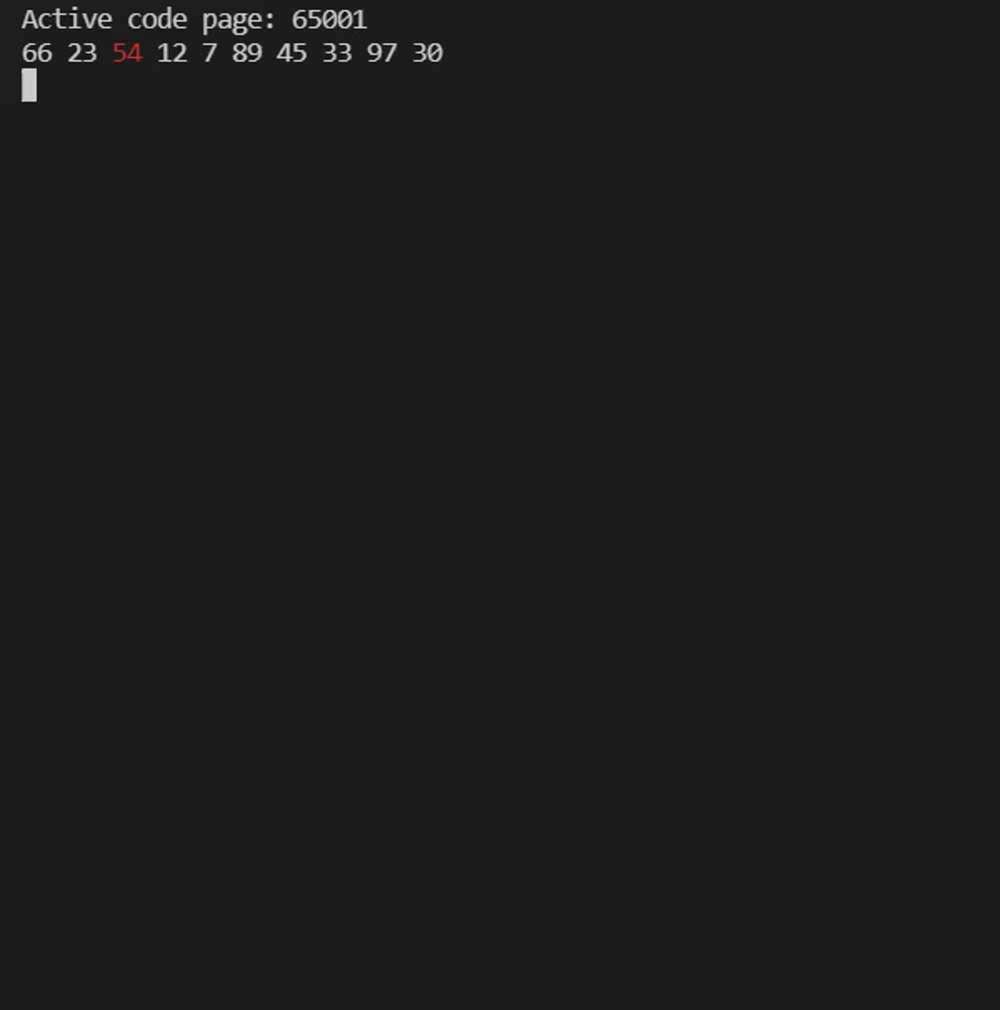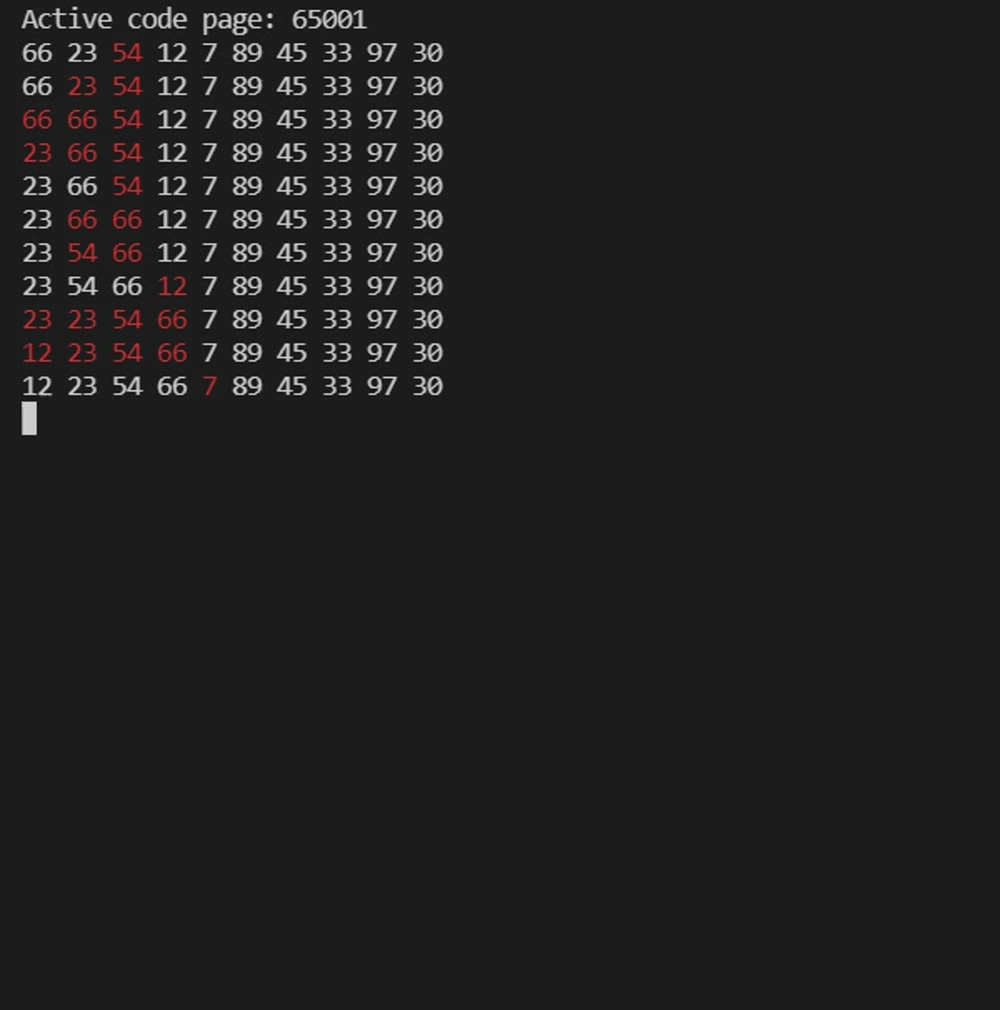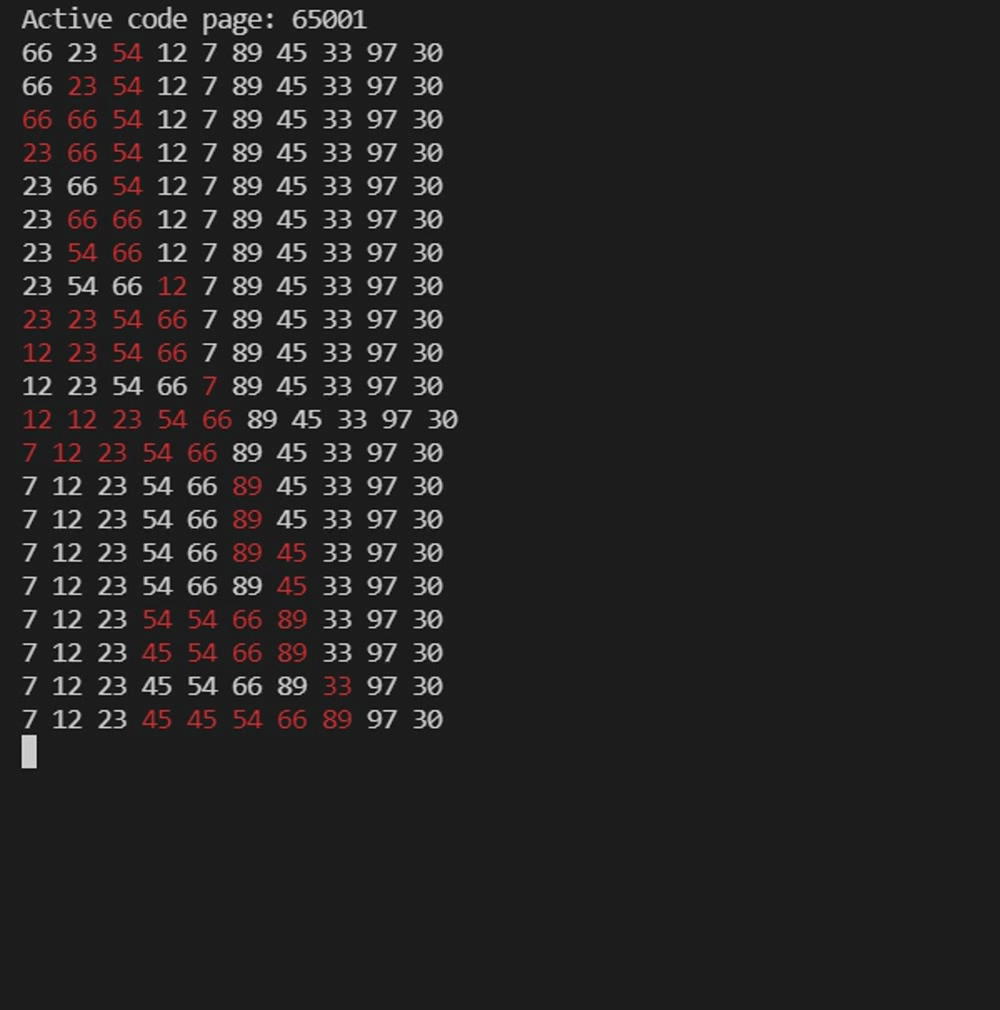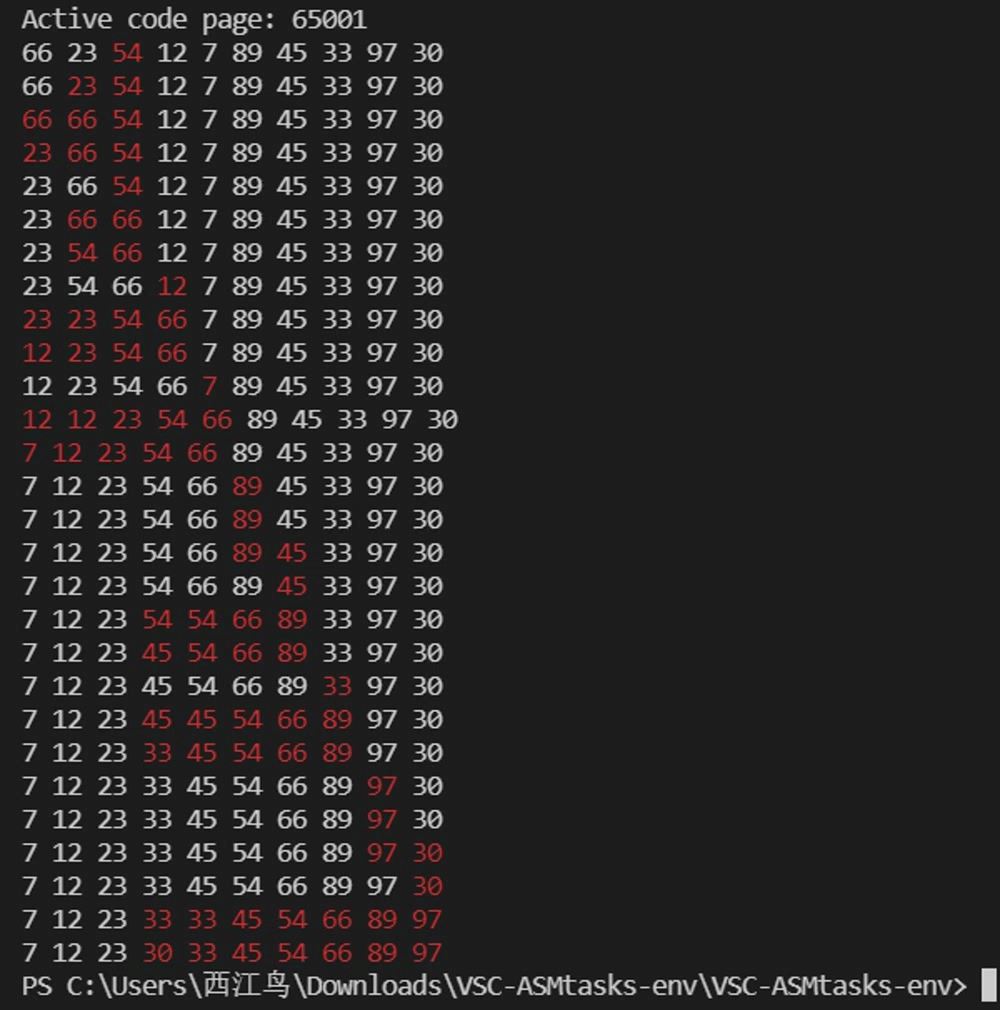
 实例测试——希尔排序

int main() {
    int arr[] = {66,23,54,12,7,89,45,33,97,30};
    int len = (int) sizeof(arr) / sizeof(*arr);
    int *colorIndex = new int[len]; //定义一个动态数组
    memset(colorIndex,0,len);       //初始化为0
    output(arr,len,colorIndex);
    shell_sort(arr, len);
    return 0;
}

注意观察不同间隔gap的组，在组内进行直接插入排序的过程。

五.归并排序

算法核心：采用分治的思想，不断将原始序列一分为二，直到一个小组内只包含一个元素。然后各小组两两合并成一个较大的组，当只剩一个小组的时候排序就完成了。合并的过程中依次从各组中选取较小的元素放入临时数组中，排序完成后将临时数组覆盖原数组即可得到排好序的序列。

时间复杂度：O(n\log _{2}n)

空间复杂度：O(n)

稳定性：稳定

 适用条件：适用于规模较大的数组排序

递归写法

//归并排序递归写法
void mergeSort_recursive(int arr[],int temp[],int start,int end)
{
    if(start>=end)
    {
        return;
    }

    int len = end-start,mid = (len>>1)+start;
    int start1 = start,end1 = mid;
    int start2 = mid+1,end2 = end;
    mergeSort_recursive(arr,temp,start1,end1);
    mergeSort_recursive(arr,temp,start2,end2);
    int k = start;      
    while(start1 <=end1 && start2 <= end2)
        {
            temp[k++] = arr[start1] < arr[start2] ? arr[start1++]:arr[start2++]; //两个小分组中选取较小值存入临时数组
        }
    while(start1 <= end1)
        {
            temp[k++] = arr[start1++];      //1号小分组没遍历完，直接接到临时数组末尾
        }
    while(start2 <= end2)
        {
            temp[k++] = arr[start2++];      //2号小分组没遍历完，，直接接到临时数组末尾
        }
    for(k = start; k <= end; k++)
        {
            arr[k] = temp[k];               //排好序的临时数组覆盖原始数组
        }
}

void merge_sort(int arr[],const int len)
{
    int *temp = new int[len];
    mergeSort_recursive(arr,temp,0,len-1);
}

 实例演示——归并排序(递归写法)

int main() {
    int arr[16];
    int len = (int) sizeof(arr) / sizeof(*arr);
    int *Randarr = getRandarray(arr,len);
    int *colorIndex = new int[len];    //定义一个动态数组
    // memset(colorIndex,0,len);       //初始化为0
    resetColor(colorIndex,len);
    cout<<"*******归并排序递归法********"<<endl;
    cout<<"原始序列:  ";
    output(arr,len,colorIndex);
    merge_sort(arr, len);
    resetColor(colorIndex,len);
    cout<<"排序序列:  ";
    output(arr,len,colorIndex);
    return 0;
}

 把原始序列递归地一分为二直到只有一个元素时才开始合并。

迭代写法

void merge_sort(int arr[],int len)
{   
    int getmin(int,int);
    int *a = arr;
    int *b = (int*)malloc(len*sizeof(int));
    for(segLength = 1;segLength < len; segLength += segLength){
        /*迭代写法与递归过程刚好相反,开始先从段长为1开始，按照段长segLength=1,2,4,8...依次合并迭代，
        直到将所有段合并为一个排好序的序列*/ 
        for(start = 0; start < len; start += 2*segLength){
            int low = start,mid = getmin(start+segLength,len),high = getmin(start+2*segLength,len);
            int k = low;
            int start1 = low,end1 =mid;
            int start2 = mid,end2 = high;
            while(start1 < end1 && start2 < end2)
                {
                    b[k++] = a[start1] < a[start2] ? a[start1++]:a[start2++];   //从各段中选取较小的元素添加到临时数组末尾
                }
            while (start1 < end1)
                {
                    b[k++] = a[start1++];   //1号段没有遍历完直接拼接到临时数组中
                }
            while(start2 < end2)
                {
                    b[k++] = a[start2++];   //2号段没有遍历完直接拼接到临时数组中
                }
        }
        
        int *temp = a;      //备份原始数组
        a= b;               //a数组中存储这一轮排序后的序列
        b = temp;           //b数组存储原始序列       
    }
    if(a != arr){
        int i;
        for(i = 0;i < len; i++)
            {
                b[i] = a[i];    //用a数组排好序的元素覆盖原始位置元素
            }
        b = a;
    }
    free(b);
}

 实例演示——归并排序(迭代写法)

int main() {
    int arr[16];
    int len = (int) sizeof(arr) / sizeof(*arr);
    int *Randarr = getRandarray(arr,len);
    int *colorIndex = new int[len];    //定义一个动态数组
    // memset(colorIndex,0,len);       //初始化为0
    resetColor(colorIndex,len);
    cout<<"*******归并排序迭代法********"<<endl;
    cout<<"原始序列:"<<endl;
    output(arr,len,colorIndex);
    merge_sort(arr, len);
    resetColor(colorIndex,len);
    output(arr,len,colorIndex);
    return 0;
}

 对比递归法，观察它们元素划分和合并的异同点。

 六.快速排序（改进的冒泡排序）

算法核心：

        在无序序列中随机选取一个元素作为枢轴(基准)，同时从左往右、从右往左两个方向进行扫描，把比枢轴小的元素交换到枢轴左边，比枢轴大的元素放在枢轴右边，一次划分可得到枢轴两侧的两个无序子序列，然后再次在左右两侧的子序列中调用快速排序算法，直到只有一个元素时递归结束。

时间复杂度：O(n\log _{2}n)

空间复杂度：O(\log _{2}n)

稳定性：不稳定

适用条件：初始序列无序

        快速排序是对冒泡排序的一种改进，只需一趟排序就可以把较大的元素放到枢轴后面，较小元素放到枢轴前面，元素一次比较的移动距离比冒泡排序远。快速排序适用于无序序列，当原始序列基本有序时快速排序退化为冒泡排序。

 递归写法

/*快速排序递归法*/


//获取枢轴下标
int getPivot(int arr[],int low,int high)
{   
    int i,j;
    int pivot = arr[low];       //一般选取无序序列的第一个元素作为枢轴
    i = low,j = high;

    while(i < j)
    {
        while(i<j && arr[j] >= pivot)  //从后往前扫描寻找比枢轴小的元素交换到枢轴前
            j--;
        arr[i] = arr[j];               //刚开始的时候arr[i]中的值已经保存在pivot,所以可以直接覆盖
        while(i < j && arr[i] <= pivot)   //从前往后扫描寻找比枢轴大的元素交换到枢轴后
            i++;
        arr[j] = arr[i];               //arr[j]中的值已经保存在上一轮的arr[i]中了,所以可以被新的arr[i]覆盖
    }

    arr[i] = pivot;  //i=j即为枢轴所在位置
    return i;       

}

void quickSort_recursive(int arr[],int low,int high)
{
    if(low < high)
    {   
        int pivot = getPivot(arr,low,high);     //获取枢轴下标
        quickSort_recursive(arr,low,pivot-1);   //枢轴左侧再进行一次快排
        quickSort_recursive(arr,pivot+1,high);  //枢轴右侧再进行一次快排

    }
}


void quickSort(int arr[],int len)
{
    quickSort_recursive(arr,0,len-1);

}

实例演示——快速排序(递归法)

int main() {
    int arr[16];
    int len = (int) sizeof(arr) / sizeof(*arr);
    int *Randarr = getRandarray(arr,len);
    int *colorIndex = new int[len];    //定义一个动态数组
    // memset(colorIndex,0,len);       //初始化为0
    resetColor(colorIndex,len);
    cout<<"*******快速排序递归法********"<<endl;
    cout<<"原始序列:  ";
    output(arr,len,colorIndex);
    quickSort(arr, len);
    resetColor(colorIndex,len);
    allsetColor(colorIndex,len);
    cout<<"排序序列:  ";
    for(int i=0;i<pivotIndex.size();i++)
        colorIndex[pivotIndex[i]]=0;
    output(arr,len,colorIndex);
    return 0;
}

 迭代写法

//定义一个结构体存储枢轴划分出来的左右子序列区间大小
typedef struct {
    int low;
    int high;
}Range;

void quickSort(int arr[],int len)
{
    int low,high;
    vector <Range>s;        //用向量储存枢轴划分出来的多个子序列
    Range range = {0,len-1};
    s.push_back(range);
    while(s.size() != 0)      //向量大小为空时说明所有枢轴划分出来的子序列全部排序完毕
    {
        low = s.back().low;
        high = s.back().high;
        int pivot = getPivot(arr,low,high);
        s.pop_back();
        if((pivot-low) >= 2)  //子序列长度大于2时才需要再次划分
            {
                s.push_back(Range{low,pivot-1});
            }
        if((high-pivot) >= 2) 子序列长度大于2时才需要再次划分
            {
                s.push_back(Range{pivot+1,high});
            }
    }
    
}

 实例演示——快速排序(迭代法)

int main() {
    int arr[16];
    int len = (int) sizeof(arr) / sizeof(*arr);
    int *Randarr = getRandarray(arr,len);
    int *colorIndex = new int[len];    //定义一个动态数组
    // memset(colorIndex,0,len);       //初始化为0
    resetColor(colorIndex,len);
    cout<<"*******快速排序递归法********"<<endl;
    cout<<"原始序列:  ";
    output(arr,len,colorIndex);
    quickSort(arr, len);
    resetColor(colorIndex,len);
    allsetColor(colorIndex,len);
    cout<<"排序序列:  ";
    for(int i=0;i<pivotIndex.size();i++)
        colorIndex[pivotIndex[i]]=0;
    output(arr,len,colorIndex);
    return 0;
}

 七.堆排序

算法核心：首先将一个无序序列建成一个大顶堆/小顶堆，然后依次输出堆顶元素(将堆顶元素交换到末尾)，并将剩余元素重新调整为一个新的堆，重复上述过程直至输出最后一个元素。

时间复杂度：O(n\log _{2}n)

空间复杂度：O(1)

稳定性：不稳定

 适用条件：适用于规模较大的数组排序

class Heap{
    public:
        int length;
        vector<int>r;
        Heap(int arr[],int len);
};

Heap :: Heap(int arr[],int len)
{
    length = len;
    for(int i = 1; i < len+1; i++)
    {
        r.push_back(arr[i]);
    }
}


//堆调整
void heapAdjust(Heap &heap,int s,int e){
    //H.r[s..e]中除H.r[s]外均满足堆的定义
    //调整H.r[s]的关键字，使H.r[s..e]成为一个小顶堆
    int temp = heap.r[s];   
    for(int j = 2*s; j <= e ; j *=2)                   //从左孩子开始,左孩子为2*s,右孩子为2*s+1
    {

        if(j < e && heap.r[j] > heap.r[j+1]) ++j;     //沿着较小的孩子向下寻找
        if(temp <= heap.r[j]) break;               //当前子树已经是堆了
  
        heap.r[s] = heap.r[j];                 //子树中最小的节点交换到子树堆顶位置
        s = j;

    }
    heap.r[s]  = temp;                        //原节点交换到孩子节点位置

}




//堆排序
void HeapSort(int arr[],int len){

    for(int i = heap.length / 2; i >= 0; --i)        //叶子节点一定是堆，则从第一个有孩子的节点即length/2开始调整，直到根节点也变成堆
    {
        heapAdjust(heap,i,heap.length-1);

    }

    for(int j = heap.length-1;j >= 1; --j)
    {
        swapValue(heap.r[0],heap.r[j]);     //把堆顶元素交换到最后并输出之

        heapAdjust(heap,0,j-1);             //将剩余节点重新调整为一个堆
       
    }

}

 实例演示——堆排序

 这里用到了二叉树的打印代码较为复杂，这里不作讨论，详情可参见：

二叉树打印代码https://blog.csdn.net/daimashiren/article/details/120312618?spm=1001.2014.3001.5501

八.计数排序

算法核心：额外申请一个计数数组 count[] 用于统计待排序序列中每个元素的个数，然后从前往后遍历计数数组依次累加各元素的计数和，得到各元素在排序序列中的实际位置下标，在临时数组output[] 中的对应位置插入各元素，直到全部元素插入完毕，再用临时数组覆盖原序列即可。

时间复杂度：O(n+k)，k为序列元素大小范围

空间复杂度：O(n+k)

稳定性：稳定

void countSort(int arr[],int len)
{
	int output[len];
   

	//初始化一个计数数组并初始化为0
	int count[RANGE + 1], i;
	memset(count, 0, sizeof(count));

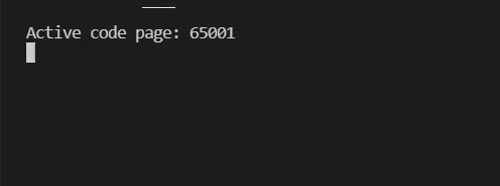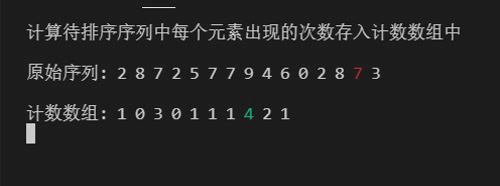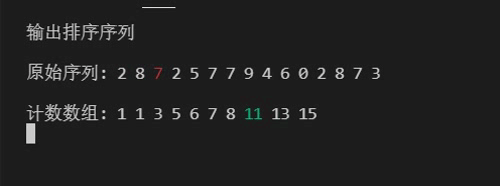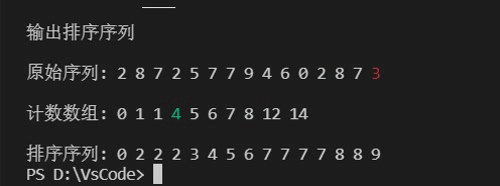
	//计算待排序序列中每个元素出现的次数存入计数数组中
	for (i = 0; i < len; ++i)
        {
            ++count[arr[i]];             //大小为arr[i]的元素个数储存在第arr[i]的位置
        }
        
   
    //从前往后遍历计数数组，确定各元素的实际下标
	for (i = 1; i <= RANGE; ++i)
		{
            count[i] += count[i - 1];
        }
 
	//输出排序序列
	for (i = 0; i < len; ++i) {
		output[count[arr[i]] - 1] = arr[i];        //output的下标从0开始,故第一个arr[i]插入的位置应该是count[arr[i]]-1
		--count[arr[i]];                           //更新下一个arr[i]应该插入的位置
	}
	
    //排好序的序列覆盖原序列
	for (i = 0; i < len; ++i)
    {
        arr[i] = output[i];
    }
		
}

实例演示——计数排序

九.基数排序

算法核心：基于计数排序，按照元素大小的个位、十位、百位...依次调用计数排序进行排序，直到全部元素有序。需要注意的是，当前位的排序是基于上一位的排序结果的。因此，如果有两个元素的当前位相同，则不能改变上一位排序的排序结果。例如下面的例子中元素909经过十位这一趟的排序后已经排在了元素924的前面，进行百位排序时不能改变这一相对顺序，所以基数排序的最后的关键一步是要从序列末尾逆序遍历排序(假设排序要得到的是从小到大的序列)。

时间复杂度：O(d*(n+rd))，rd为数据基数(十进制/二进制)，d = O(log_{rd}k)，k为待排序列中的最大值（每一趟分配O(n)，每一趟收集O(rd)，共d趟→O(d*(n+rd)）

空间复杂度：O(rd)

稳定性：稳定

适用条件：适用于元素数目n很大且值较小的序列

void countSort(int arr[], int len, int r)       //r为当前排序的基数位(个位，百位...)
{
    int output[len]; 
    int i, count[10] = { 0 };
 
    for (i = 0; i <len; i++)
        {
            count[(arr[i] / r) % 10]++;        //如果后几次排序中多次出现arr[i]/r%10=0,相当于前面几次排序中已经排好了，只需要“照抄”就行
        }

    for (i = 1; i < 10; i++)
        {
            count[i] += count[i - 1];
        }
 
    for (i =len - 1; i >= 0; i--)              //逆序遍历是关键，当前位相同时，不能改变上一位排序的排序结果
        {
        output[count[(arr[i] / r) % 10]-1] = arr[i];
        count[(arr[i] / r) % 10]--;
        }
 
    for (i = 0; i < len; i++)
        {
            arr[i] = output[i];
        }
}


void radixSort(int arr[],int len){
    int max = getMax(arr,len);
   
    for(int r = 1; max / r >0; r *= 10)     //从个位开始比较，依次比较十位，百位...
    {
        //调用计数排序完成一次排序
        countSort(arr,len,r);
    }

}

实例演示——基数排序

 

 十.桶排序

算法核心：额外申请一个向量数组 b[] 用于实现对序列元素的区间划分，采用一定的规则将不同元素装入各自对应的桶中，然后再在各自的桶内进行排序，将排序好的各个桶按照先后次序依次连接即可得到一个有序序列。

时间复杂度：O(n)

空间复杂度：O(n)

稳定性：不稳定(取决于桶内排序的算法，通常采用的是快速排序)

适用条件：1.序列元素处在一定的取值范围内

                  2.序列元素在各个桶之间的分布较为均匀

        桶排序在最佳情况下时间复杂度可以达到O(n)，但对序列元素的分布和大小要求较为严格，当序列元素在各桶间的分布较不均匀，即存在有的桶内元素很多，有的桶内元素较少时，桶排序将退化为O(nlog_{2}n)的算法。

void bucketSort(float arr[], int len)
{
   
    // 建立len个桶
	vector<float> b[len];

	// 将各元素插入桶中
	for (int i = 0; i < len; i++) {
		int bi =len * arr[i];            // 桶的编号
		b[bi].push_back(arr[i]);
	}

	//分别进行桶内排序
	for (int i = 0; i < len; i++)
		sort(b[i].begin(), b[i].end());         //C++中的sort底层是采用快速排序实现的

	// 连接各个桶
	int index = 0;
	for (int i = 0; i < len; i++)
        for (int j = 0; j < b[i].size(); j++)
            arr[index++] = b[i][j];
}

实例演示——桶排序

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

daimashiren

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值