【深度学习】卷积神经网络的实现与理解

本系列由斯坦福大学CS231n课后作业提供
CS231N - Assignment2 - Q4 - ConvNet on CIFAR-10

---

问题描述：使用IPython Notebook（现版本为jupyter notebook，如果安装anaconda完整版会内置），在ConvolutionalNetworks.ipynb文件中，你将实现几个卷积神经网络中常用的新层。使用CIFAR-10数据，训练出一个深度较浅的卷积神经网络，最后尽你所能训练出一个最佳的神经网络。

---

任务

实现卷积神经网络卷积层的前向计算与反向传导
实现卷积神经网络池化层的前向计算与反向传导
卷积层与池化层的加速

---

卷积神经网络结构

常规神经网络的输入是一个向量，经一系列隐层的转换后，全连接输出。在分类问题中，它输出的值被看做是不同类别的评分值。
神经网络的输入可不可以是图片呢？
常规神经网络对于大尺寸图像效果不尽人意。图片的像素点过多处理起来极为复杂。因此在处理图片的过程中较为合理地降维成为一个模糊的研究方向。因此基于神经网络结构产生了一个新的神经网络层结构，我们称之为卷积神经网络。
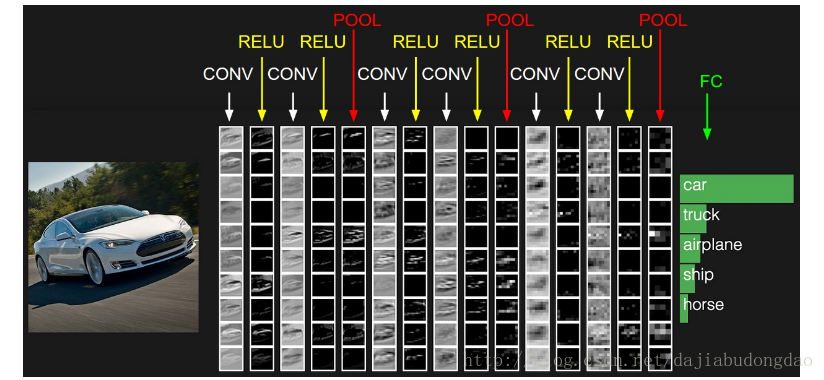
下图是多层卷积神经网络的一种结构：

可以看出，网络结构开始为“卷积层（CONV），relu层（RELU），池化层（POOL）”C-R-P周期循环，最后由全连接层（FC）输出结果。

注：实际应用的过程中常常不限于C-R-P循环，也有可能是C-C-R-P等等

设激活函数$f_{sigmoid}(-)$，池化操作$pool(-)$,x为输入数据代表图像像素矩阵，w为权重代表过滤层（卷积核），b代表偏置。C-R-P周期则有下面的计算公式：
$$x_j^l=f_{relu}(pool(\sum _{i\in M_j}{x}_i^{l-1}\ast w_{ij}^l+b_j^l))$$
卷积神经网络的理解比较困难，为了更好地了解，我们先讲解过程再讨论实际作用。

卷积层的朴素（无加速算法）实现与理解

（在实际应用过程中，一般使用加速过程处理的卷积层，这里表现的是原始卷积版本）
###卷积层元素
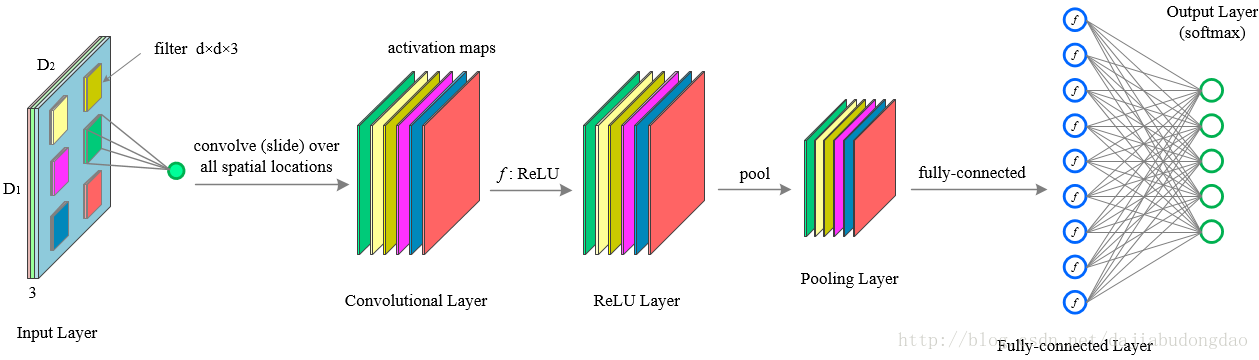
下图是卷积层的元素：输入图片与过滤参数。

输入图片（image）：输入层（Input Layer）有3个深度（D1，D2，D3，通常代表图片的三个通道RGB）。我可以将每个深度独立出来，看成三幅图片。图片的大小为32*32。

过滤参数（filter）：过滤器有很多称呼，如“卷积核”、“过滤层”或者“特征检测器”。不要被名词坑了。过滤器也有3个深度（D1，D2，D3），就是与输入图片的深度进行一一对应，方便乘积操作。过滤器窗口一般比输入图片窗口小。
###卷积层的前向计算
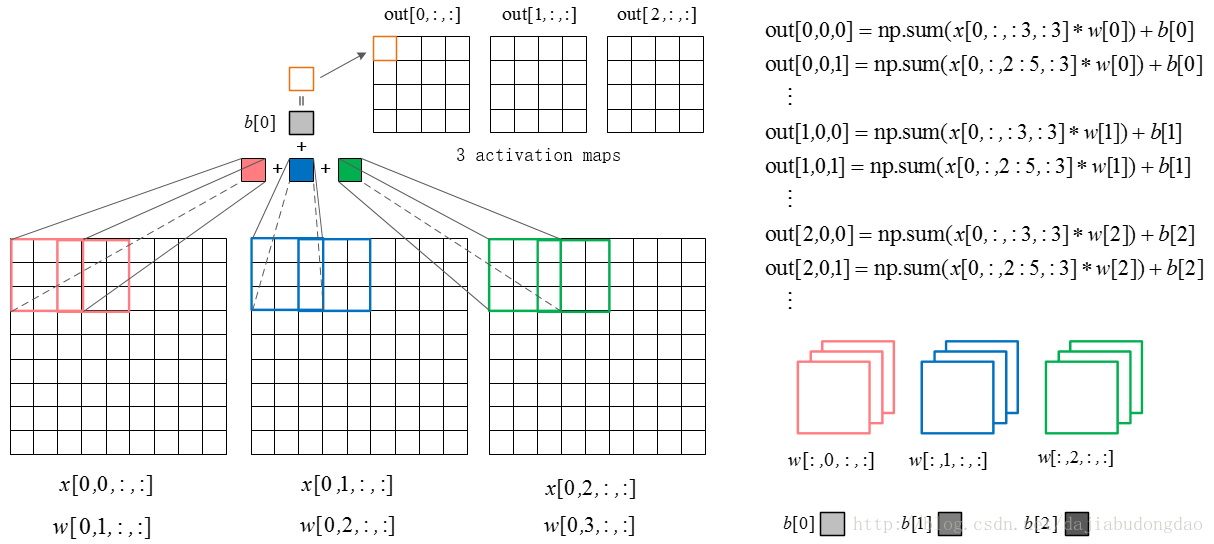
下图是卷积层的具体实现方法。

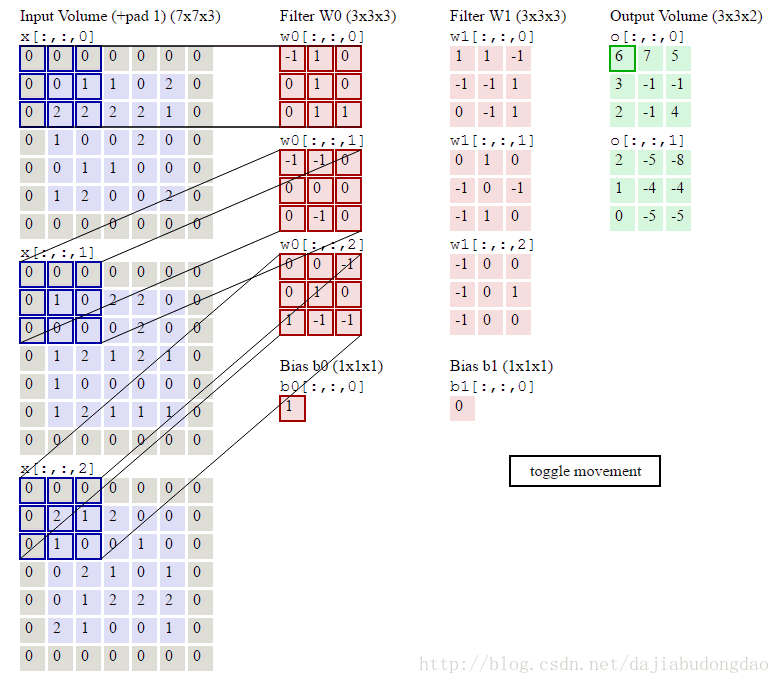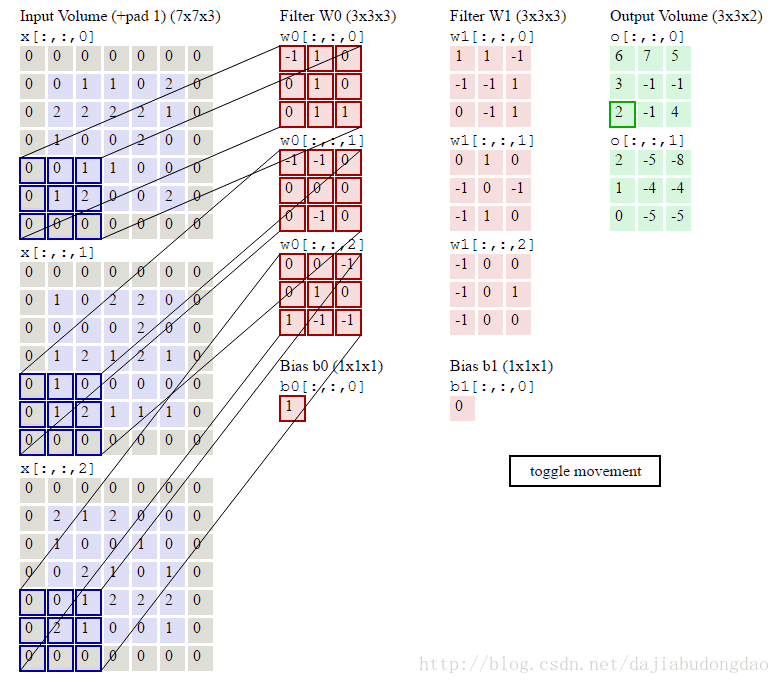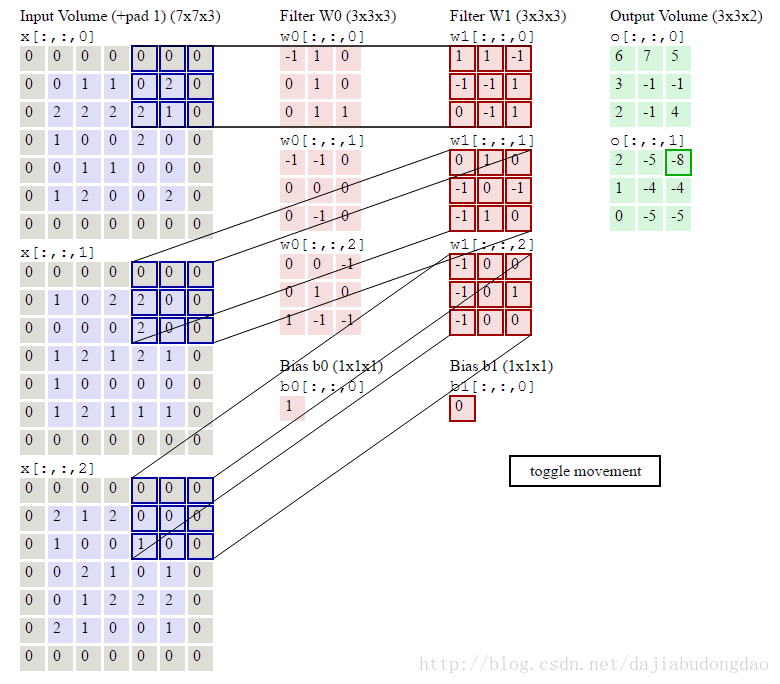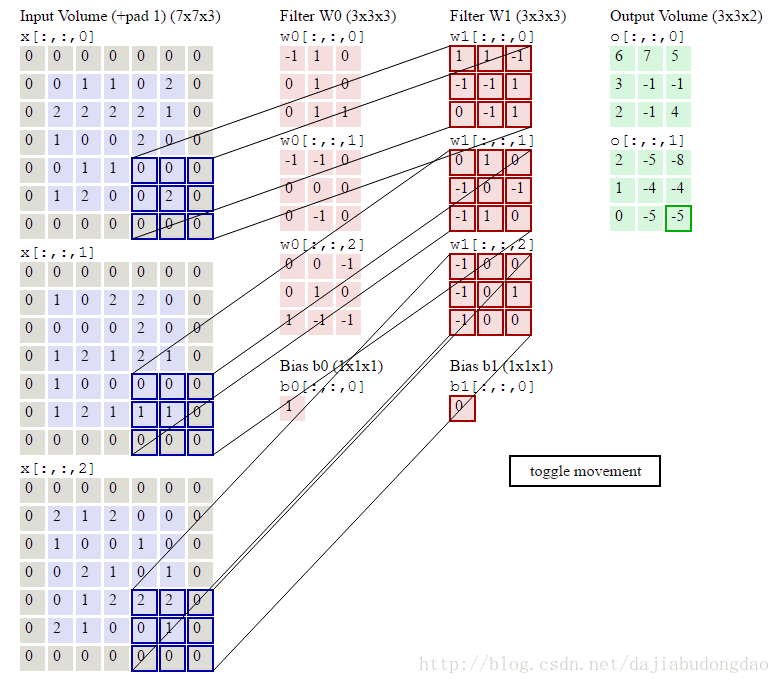
x代表图片image矩阵，w代表过滤层矩阵。过滤器与image一样窗口大小的部分乘积求和，这就是卷积过程。下面的动图就是卷积过程。

上图中我们看到每次窗口移动2格。这2格就是每次卷积的移动步长。
我们看到原来的图片在周围填充了一圈0。填充0的宽度即为每次卷积的填充宽度
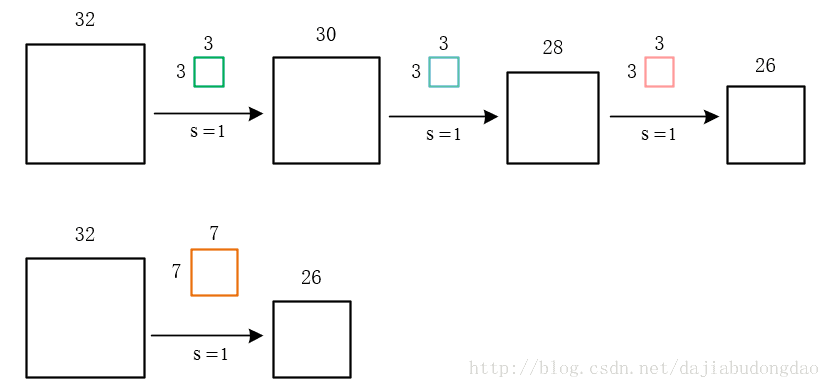
移动步长很好理解，但为什么要填充呢？假设我们不填充。如下图：

会发现每次卷积之后都会有维度降低。浅层卷积网络可能没有什么问题。但是深层卷积可能在网络没到最后的时候维度即降为0。
这显然不是我们所希望的。
当然，如果有意愿用卷积计算去降维也可以，不过我们更喜欢用池化层的池化操作降维。为甚？我们必须先了解卷积层的作用。

卷积层正向卷积过程代码实现

def conv_forward_naive(x, w, b, conv_param):
    """
    A naive implementation of the forward pass for a convolutional layer.

    The input consists of N data points, each with C channels, height H and
    width W. We convolve each input with F different filters, where each filter
    spans all C channels and has height HH and width HH.

    Input:
    - x: Input data of shape (N, C, H, W)
    - w: Filter weights of shape (F, C, HH, WW)
    - b: Biases, of shape (F,)
    - conv_param: A dictionary with the following keys:
      - 'stride': The number of pixels between adjacent receptive fields in the
        horizontal and vertical directions.
      - 'pad': The number of pixels that will be used to zero-pad the input.

    Returns a tuple of:
    - out: Output data, of shape (N, F, H', W') where H' and W' are given by
      H' = 1 + (H + 2 * pad - HH) / stride
      W' = 1 + (W + 2 * pad - WW) / stride
    - cache: (x, w, b, conv_param)
    """
    ###########################################################################
    # TODO: Implement the convolutional forward pass.                  #
    # Hint: you can use the function np.pad for padding.               #    ###########################################################################
    N, C, H, W = x.shape
    F, C, HH, WW = w.shape
    stride = conv_param['stride']
    pad = conv_param['pad']
    
    ##计算卷积后新矩阵的大小并分配全零值占位
    new_H = 1 + int((H + 2 * pad - HH) / stride)
    new_W = 1 + int((W + 2 * pad - WW) / stride)
    out = np.zeros([N, F, new_H, new_W])

    ##卷积开始
    for n in range(N):
        for f in range(F):
            ##临时分配(new_H, new_W)大小的全便宜香卷积矩阵，（即提前加上偏移项b[f]）
            conv_newH_newW = np.ones([new_H, new_W])*b[f]
            for c in range(C):
                ##填充原始矩阵，填充大小为pad，填充值为0
	            pedded_x = np.lib.pad(x[n, c], pad_width=pad, mode='constant', constant_values=0)
                for i in range(new_H):
                    for j in range(new_W):
                        conv_newH_newW[i, j] +=  np.sum( pedded_x[i*stride:i*stride+HH, j*stride:j*stride+WW] * w[f,c,:,:] )
                out[n,f] = conv_newH_newW
    ###########################################################################
    #                             END OF YOUR CODE                     #
###########################################################################
    cache = (x, w, b, conv_param)
    return out, cache

###卷积层的个人理解
对卷积层的作用，很多人的说法莫衷一是。我这里谈谈自己的理解。
####1. 实现某像素点多通道以及周围信息的整合
说白了就是将一个像素与其周围的点建立联系。我们用将一点及其周边“卷”起来求和计算。那么每一层卷积必然是将一个像素点与周围建立联系的过程。

这么说起来“Convolution”翻译为“卷和”更恰当，其实卷积的“积”是积分的意思

####2. 我们先讲一个丧心病狂的故事
如果你每天玩游戏不陪女朋友，那么女朋友每天都要扇你一巴。打你一巴掌后，脸的一部分就肿了。你的脸就是图片，女朋友的巴掌就是卷积核层。每打一巴掌，相当于“卷积核”作用脸部一个地方“做卷积”。脸肿了相当于脸部“卷积后”输出的结果。
如果有一天，女友忍无可忍，连续扇你嘴巴，那么问题就出现了。上一次扇你鼓起来的包还没消肿，第二个巴掌就来了。女友不断扇你，卷积不地作用在你脸上，效果不断叠加了，这样这些效果就可以求和了。

女友再狠一点，频率越来越高，以至于你都辨别不清时间间隔了。那么，求和就变成积分了。这就是“卷积”一词的由来。

女友打你在不同的位置，自然会有不同的身体反应。根据打你后卷积后身体的反应卷积结果可以判断出打到什么位置了。

身体反应(卷积结果)	可能推论
肿了	打到脸了
红了	打到肚子了
没反应	打到骨头了
女友手疼	打到骨刺了
更爱她了	变态
没有感觉	单身狗的幻想

这么一解释卷积层的解释果然很明显。。。。嗯，对。。。。我自己都信了。。。。

3. 图像处理中模板的概念

在传统图像处理中，模板即一个矩阵方块。在这里你可以认为是卷积核，计算为方法为卷积运算。如下面的一个模板

$$\frac{1}{9}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$
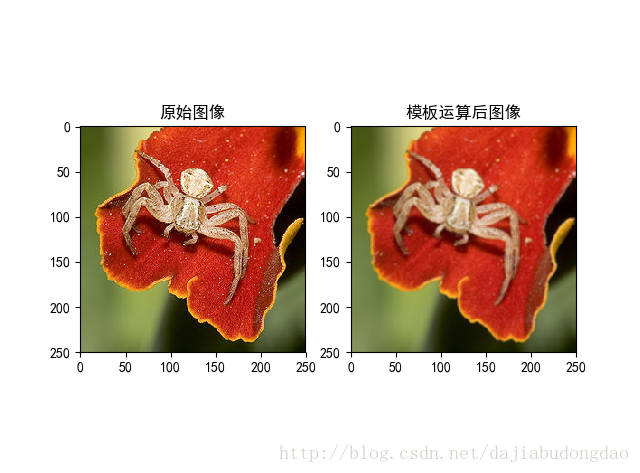
一幅图片经过它的卷积运算，可以得到这样的结果。

上面的那种模板就是“低通滤波模板”的一种。
通过改变方阵的数值与大小，可以生成很多新鲜的模板。如“高通滤波模板”，“边缘检测模板”，“匹配滤波边缘检测模板”等等。。
那么问题来了：我们该在什么时候，用什么数值的模板？对传统的模板选择，凭借的是算法工程师的经验。但现在，我们不怕了!~~~~~~深度学习帮我们训练模板的参数。图片在卷积神经网络的一次前向过程，相当于对图像做一次特定的处理。

###卷积层反向求导
前面我们介绍了卷积层的前向计算。大致了解了卷积的作用，但是神经网络的参数是怎么来的？参数的获取是一个迭代的训练的过程，每次反向传播是纠正参数，减小误差。（具体细节请看别人关于神经网络“前向计算，反向传播”的讲解。）
上文提到了C-R-P周期计算公式。
$$x_j^l=f_{relu}(pool(\sum _{i\in M_j}{x}_i^{l-1}\ast w_{ij}^l+b_j^l))$$
$f_{relu}(-)$为relu激活函数，池化操作用$pool(-)$表示,x为输入数据代表图像像素矩阵，w为权重代表过滤器（卷积核），b代表偏置。
编写卷积层反向传播时，暂时不用考虑池化层，与激活函数。我们可以用g()代指卷积层后所有的操作。所以这一层的反向对x求导可以简化为如下操作。
$$\begin{gathered} g(x\ast w+b)=g(out) \\ out=x\ast w+b \\ \frac{\partial g}{\partial x}=\frac{\partial g}{\partial out}\ast \frac{\partial out}{\partial x} \end{gathered}$$
在斯坦福CS231n课程作业中，把无实际用处的g忽略。记$dx=\frac{\partial g}{\partial x},dout=\frac{\partial g}{\partial out}$。
对于中国大陆学生来说这是一个深渊巨坑的记法。在高等数学教材里。dout，dx有专门的含义。但这里我们要遵循老师的记法。
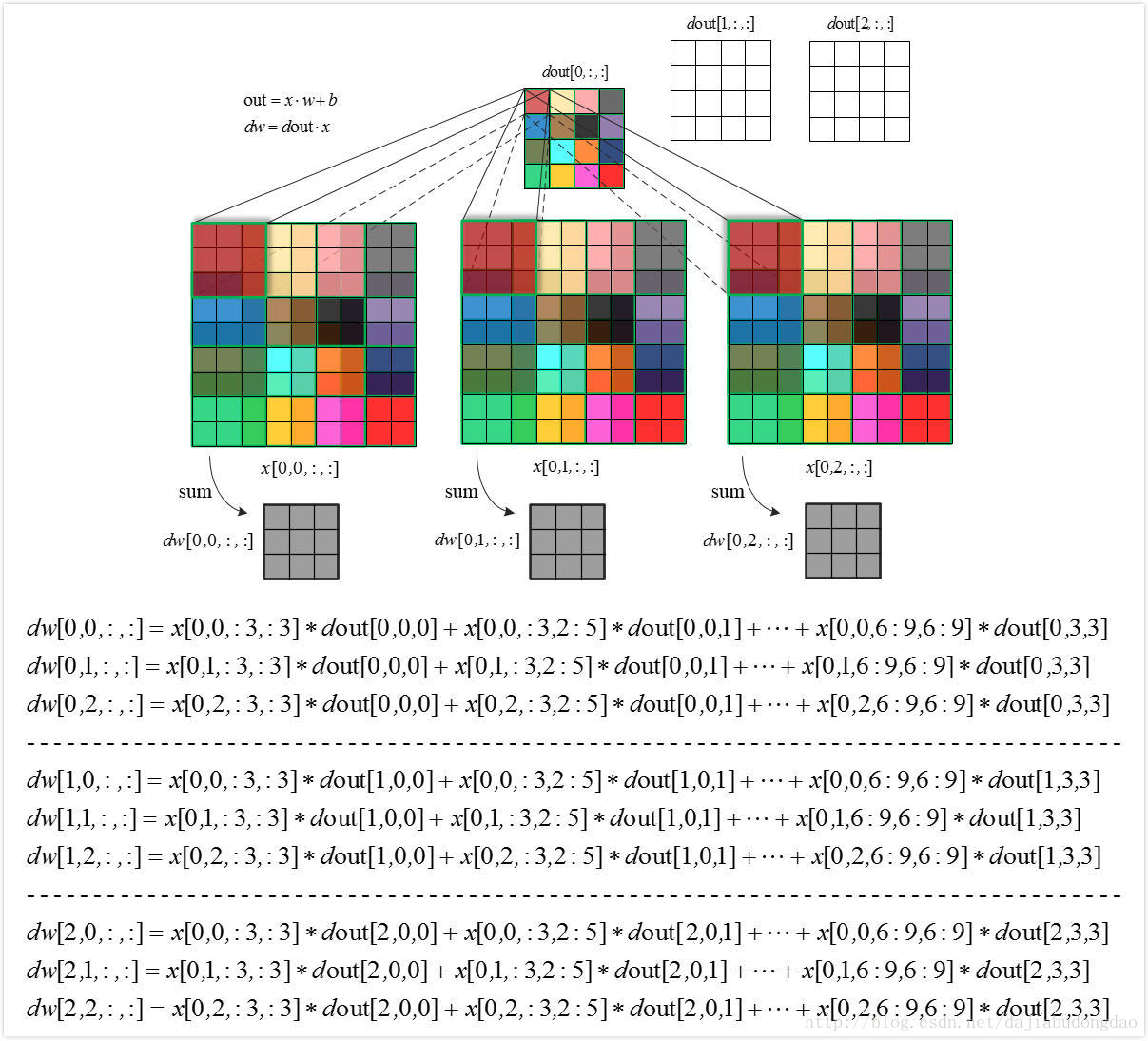
下图为卷积层反向求导的过程图片。

卷积层反向求导过程代码实现

def conv_backward_naive(dout, cache):
    """
    A naive implementation of the backward pass for a convolutional layer.

    Inputs:
    - dout: Upstream derivatives.
    - cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive

    Returns a tuple of:
    - dx: Gradient with respect to x
    - dw: Gradient with respect to w
    - db: Gradient with respect to b
    """
   ###########################################################################
    # TODO: Implement the convolutional backward pass.             #
###########################################################################
    # 数据准备
    x, w, b, conv_param = cache
    pad = conv_param['pad']
    stride = conv_param['stride']
    F, C, HH, WW = w.shape
    N, C, H, W = x.shape
    N, F, new_H, new_W = dout.shape

    # 下面，我们模拟卷积，首先填充x。
    padded_x = np.lib.pad(x,
                          ((0, 0), (0, 0), (pad, pad), (pad, pad)),
                          mode='constant',
                          constant_values=0)
    padded_dx = np.zeros_like(padded_x)  # 填充了的dx，后期去填充即可得到dx
    dw = np.zeros_like(w)
    db = np.zeros_like(b)

    for n in range(N):  # 第n个图像
        for f in range(F):  # 第f个过滤器
            for i in range(new_H):
                for j in range(new_W):
                    db[f] += dout[n, f, i, j] #求导为1，无争议
                    dw[f] += padded_x[n, :, i*stride : HH + i*stride, j*stride : WW + j*stride] * dout[n, f, i, j]
                    padded_dx[n, :, i*stride : HH + i*stride, j*stride : WW + j*stride] += w[f] * dout[n, f, i, j]
    # 反填充
    dx = padded_dx[:, :, pad:pad + H, pad:pad + W]
    ###########################################################################
    #                             END OF YOUR CODE                 #  ###########################################################################
    return dx, dw, db

池化层的朴素（无加速算法）实现与理解

池化层的前向计算

在“卷积层需要填充”这一部分我们就说过：卷积层负责像素间建立联系，池化层负责降维。从某种层度上来说，池化操作也算是一种不需要填充操作的特殊的卷积操作。
池化操作也需要过滤器（也有翻译为池化核），每次过滤层移动的距离叫做步长。
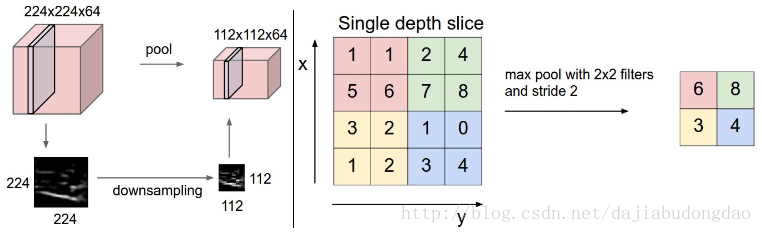
不过在池化操作中，过滤器与原图可以不做卷积运算，仅仅是降维功能。下图就表示过滤器选择窗口最大项的**“最大池化操作”**。

最大池化操作的前向计算

基于卷积的经验，很快地写出最大池化操作的前向计算与反向求导的代码。

def max_pool_forward_naive(x, pool_param):
    """
    A naive implementation of the forward pass for a max pooling layer.

    Inputs:
    - x: Input data, of shape (N, C, H, W)
    - pool_param: dictionary with the following keys:
      - 'pool_height': The height of each pooling region
      - 'pool_width': The width of each pooling region
      - 'stride': The distance between adjacent pooling regions

    Returns a tuple of:
    - out: Output data
    - cache: (x, pool_param)
    """
    ###########################################################################
    # TODO: Implement the max pooling forward pass                      #
###########################################################################
    # 准备数据
    N, C, H, W = x.shape
    pool_height = pool_param['pool_height']
    pool_width  = pool_param['pool_width']
    pool_stride = pool_param['stride']
    new_H = 1 + int((H - pool_height) / pool_stride)
    new_W = 1 + int((W - pool_width) / pool_stride)

    out = np.zeros([N, C, new_H, new_W])
    for n in range(N):
        for c in range(C):
            for i in range(new_H):
                for j in range(new_W):
                    out[n,c,i,j] = np.max(x[n, c, i*pool_stride : i*pool_stride+pool_height, j*pool_stride : j*pool_stride+pool_width])
###########################################################################
    #                             END OF YOUR CODE                            #
###########################################################################
    cache = (x, pool_param)
    return out, cache

最大池化的反向求导

def max_pool_backward_naive(dout, cache):
    """
    A naive implementation of the backward pass for a max pooling layer.

    Inputs:
    - dout: Upstream derivatives
    - cache: A tuple of (x, pool_param) as in the forward pass.

    Returns:
    - dx: Gradient with respect to x
    """
###########################################################################
    # TODO: Implement the max pooling backward pass                     #
###########################################################################
    # 数据准备
    x, pool_param = cache
    N, C, H, W = x.shape
    pool_height = pool_param['pool_height']
    pool_width  = pool_param['pool_width']
    pool_stride = pool_param['stride']
    new_H = 1 + int((H - pool_height) / pool_stride)
    new_W = 1 + int((W - pool_width) / pool_stride)
    dx = np.zeros_like(x)
    for n in range(N):
        for c in range(C):
            for i in range(new_H):
                for j in range(new_W):
                    window = x[n, c, i * pool_stride: i * pool_stride + pool_height,j * pool_stride: j * pool_stride + pool_width]
                    dx[n, c, i * pool_stride: i * pool_stride + pool_height, j * pool_stride: j * pool_stride + pool_width] = (window == np.max(window))*dout[n,c,i,j]
###########################################################################
    #                             END OF YOUR CODE                            #
###########################################################################
    return dx

三明治卷积层（Convolutional “sandwich” layers）

“三明治”卷积层是我得到资料是斯坦福大学CS231n的专门讲法，其实就是将多个操作组合成一个常用模式。前文我一直说的C-R-P组合，可以看做一种三明治卷积层。卷积神经网络在实际应用上，也往往跳过底层实现，直接面向组合操作。
在文件cs231n/layer_utils.py 里keras的源码里。都会找到这样的“三明治”卷积层。它们的简化了复杂深度学习神经网络的实现。