矩阵快速幂模板

基础知识：

（1）矩阵乘法

简单的说矩阵就是二维数组，数存在里面，矩阵乘法的规则:A*B=C

其中c[i][j]为A的第i行与B的第j列对应乘积的和，即:

（2）矩阵快速幂模板

       就是算A^n，就是把快速幂算法中的乘法改成矩阵的乘法就可以了

代码：

#include<iostream>
#include<cstring>
using namespace std;
const int N=5;
struct mat{
	int m[N][N];
}init;
void Init()
{
	init.m[0][0]=1;
	init.m[0][1]=2;
	init.m[1][0]=2;
	init.m[1][1]=1;
}
mat Mul(mat a,mat b,int n)
{
	mat c;
	memset(c.m,0,sizeof(c.m));
	for(int i=0;i<n;i++)
	for(int j=0;j<n;j++)
	for(int k=0;k<n;k++)
	  c.m[i][j]+=a.m[i][k]*b.m[k][j];
	return c;
}
mat quickpow(mat a,int n)
{
	mat res;
	int k=n;
    memset(res.m,0,sizeof(res.m));
    for(int i=0;i<n;i++) res.m[i][i]=1;
    while(k)
    {
    	if(k&1) res=Mul(a,res,n);
    	a=Mul(a,a,n);
    	k>>=1;
	}
	return res;
}
int main()
{
	int n;
	cin>>n;
	Init();
	mat t=quickpow(init,2);
	cout<<t.m[0][0]<<" "<<t.m[0][1]<<endl;
	cout<<t.m[1][0]<<" "<<t.m[1][1]<<endl;
	return 0;
}

例一:http://poj.org/problem?id=3070
题目：斐波那契数列f(n),给一个n，求f(n)%10000,n<=1e9;

(这题是可以用fibo的循环节去做的，不过这里不讲，反正是水题)

矩阵快速幂是用来求解递推式的，所以第一步先要列出递推式:

 f(n)=f(n-1)+f(n-2)

第二步是建立矩阵递推式，找到转移矩阵:

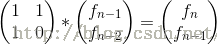,简写成T * A(n-1)=A(n)，T矩阵就是那个2*2的常数矩阵，而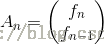

这里就是个矩阵乘法等式左边:1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);

这里还是说一下构建矩阵递推的大致套路,一般An与A(n-1)都是按照原始递推式来构建的，当然可以先猜一个An,主要是利用矩阵乘法凑出矩阵T,第一行一般就是递推式，后面的行就是不需要的项就让与其的相乘系数为0。矩阵T就叫做转移矩阵(一定要是常数矩阵),它能把A(n-1)转移到A(n);然后这就是个等比数列，直接写出通项:此处A1叫初始矩阵。所以用一下矩阵快速幂然后乘上初始矩阵就能得到An,这里An就两个元素(两个位置)，根据自己设置的A(n)对应位置就是对应的值，按照上面矩阵快速幂写法，res[1][1]=f(n)就是我们要求的。

给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

2.f(n)=c^n-f(n-1) ；（c是常数）