模态逻辑
(本文来源:http://zh.wikipedia.org/wiki/模态逻辑)
维基百科,自由的百科全书
模态逻辑 ,或者叫(不很常见)内涵逻辑 ,是处理用模态如“可能”、“或许”、“可以”、“一定”、“必然”等限定的句子的逻辑 。模态逻辑可以用语义的“内涵 性”来描述其特征: 复杂公式的真值不能由子公式的真值来决定的。允许这种决定性的逻辑是“外延 性的”,经典逻辑就是外延性的例子。模态算子不能使用外延语义来形式化: “乔治·布什 是美国总统”和“2 + 2 = 4”是真的,但是“乔治·布什必然是美国总统”是假的,而“2 + 2 = 4 是必然的”是真的。
形式模态逻辑使用模态判决算子 表示模态。基本的模态算子 是  和
和  。(有时分别使用“L”和“M”)。它们的意义依赖于特定的模态逻辑,但它们总是以相互定义的方式来定义:
。(有时分别使用“L”和“M”)。它们的意义依赖于特定的模态逻辑,但它们总是以相互定义的方式来定义:
目录[隐藏 ] |
真势模态
在真势模态逻辑(就是说必然性和可能性的逻辑)中  表示必然性 ,而
表示必然性 ,而  表示可能性 。所以 Jones 有兄弟是“可能的”,当且仅当 Jones “没”有兄弟是“非必然的”。
表示可能性 。所以 Jones 有兄弟是“可能的”,当且仅当 Jones “没”有兄弟是“非必然的”。
句子被认定为
- 可能的 如果它“可能”为真(不管实际上是真是假);
- 必然的 如果它“不可能”为假;
- 偶然的 如果它“不是”必然为真,就是说,可能为真可能为假。偶然的真理是“实际上”为真,但“可能曾经不是”的真理。
其他模态
认识
模态逻辑最经常用来谈论所谓的“真势模态 ”: “...是必然的”或者“....是可能的”,这些模态(包括形而上学模态 和逻辑模态 )最容易混淆于认识模态 (来自希腊语 episteme, 知识):“...确实是真的” 和“...(对给定的可获得的信息)或许是真的”。在普通的话语中这两种模态经常用类似的词来表达;下列对比可能有所帮助:
一个人 Jones 可以合理的“同时”说出: (1)“我确信大脚怪 不 可能存在”,还有(2)“大脚怪存在的确是可能的”。Jones 通过(1)表达的意思是,对于给定的所有可获得的信息,大脚怪存在与否是没有疑问的。这是一个认识上的断言。通过(2)表达的意思是这个事物可能曾是其它 样子的。他的意思不是“就我所知而言,大脚怪可能存在”。(所以这不矛盾于(1))。而是,他做了一个“形而上学”上的断定,“即使我不知道,大脚怪存在 仍是可能的”。
在其他方面,Jones 可以说 (3)“哥德巴赫猜想 可 能为真,也可能为假”,还有(4) “如果它是真的,则它必然是真的,不可能是假的”。这里 Jones 的意思是,“就他所知而言,它为真为假都是在认识上可能的(哥德巴赫猜想仍未被证明是真还是假)。但是如果有这么一个证明(至今仍未发现),则哥德巴赫猜 想为假在逻辑上是不可能的”。逻辑上的可能性是一种“真势”(alethic)可能性;(4)做了对一个数学真理曾经为假是否可能的一个断言,而(3)只 做了对“就 Jones 所知而言”这个论断被证实为假是否可能的一个断言,所以 Jones 还是不自相矛盾。
认识上的可能性还以一种非形而上学的方式关注真实世界。形而上学的可能性以“可能曾是”的方式关注世界,而认识上的可能性以(就我所知而言)“可能 正是”的方式关注世界。比如,我想知道在离开前是否要带把伞。如果你告诉我“外面可能在下雨” -- 在一种“认识上可能”的意义上--那么这会影响我是否带伞的决定。但是如果你告诉我“外面下雨是可能的” -- 在一种“形而上学上可能”的意义上--那么我从这种大道理中没有得到任何启示。
大量的哲学文献关心“真势”而非“认识”模态。(实际上,其中大多数关心一种最广泛的真势模态,就是逻辑可能性 )。这不是说真势可能性比我们日常用的认识可能性更重要(考虑上面决定是否带伞的例子)。只是说在哲学研究中的优先权不是日常生活中的重要性带来的。
道义和时间
言语中有一些类似的模式,尽管不大可能与真势模态混淆但仍密切的相关。其一是有关时间的谈论。明天可能会下雨,但也可能不下好像是合理的;在另一方 面,如果昨天下雨了,如果实际上已经下了,则说“昨天可能没有下雨”就不是完全正确的。过去好像“固定的”或必然的,而将来在某种程度上不是。很多哲学家 和逻辑学家认为这种推理不是很好;但是我们经常以这种方式谈话,所以最好有一种逻辑能捕获它的结构。类似的有关道德的谈论,或者说义务 和规范 一般好像也有模态结构。在“你必须这么做”和“你可以这么做”之间的区别看起来很像在“这是必然的”和“这是可能的”之间的区别。这种逻辑叫做道义逻辑 ,“道义”来自希腊语 duty。
模态逻辑的释义
在模态逻辑的最常见解释中,你要考虑“所有逻辑上可能的 世界”。如果一个陈述在所有可能世界 中是真的,则它是必然的真理。如果一个陈述碰巧在我们的世界中是真的,但不是在所有可能世界中是真的,则它是偶然的真理。在某些(不是必须在我们自己的)可能世界中是真的陈述叫做可能的真理。
这种"可能世界"是否是解释模态逻辑的最佳方式,怎样在文字上接受这种方言,是形而上学的鲜活的问题。例如,可能世界的方言可以把关于大脚怪的断言 翻译为“有某个可能世界,在其中大脚怪存在”。要主张大脚怪的存在性是可能的,但不是现实的,你可以说“有某个可能世界,在其中大脚怪存在;但是在现实世 界中,大脚怪不存在”。但是对使模态断言对我们负责的那个东西是什么仍是不清楚的。我们真的要宣称可能世界的存在性吗?它在每一点都同我们的现实世界一样 真实,却惟独不是现实的。David Lewis 强硬的说就是这样,可能世界同我们自己的世界一样真实。这种立场叫做“模态现实主义 ”。不足为奇的,多数哲学家不愿意接受这种特别的学说,在搜寻一种可替代的方式来释义我们的模态断言所蕴含的本体论承诺。
公理系统
有很多有不同性质的模态逻辑。在其中很多必然性和可能性的概念满足下列 德·摩根定律 的联系:
- " X 是 非必然的 " 等价于 "非 X 是 可能的 "。
- " X 是 非可能的 " 等价于 "非 X 是 必然的 "。
尽管模态逻辑教科书比如 Hughes 和 Cresswell 的《A New Introduction to Modal Logic》覆盖了这个定律不成立的一些系统。
模态逻辑向命题逻辑 的“合式公式”增加上必然性和偶然性。在一些记号中“必然的 p”使用“方块”(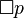 )表示,而“可能的 p”使用“菱形”(
)表示,而“可能的 p”使用“菱形”( )表示。无论是什么样的记号,两个算子是以相互定义的方式定义的:
)表示。无论是什么样的记号,两个算子是以相互定义的方式定义的:
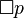 (必然的 p) 等价于
(必然的 p) 等价于  (非可能的非 p)
(非可能的非 p) (可能的 p) 等价于
(可能的 p) 等价于 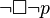 (非必然的非-p)
(非必然的非-p)
因此, 和
和  叫做对偶算子。
叫做对偶算子。
要建立模态逻辑的可用系统,必须向命题逻辑的增加什么公理是非常有争议的主题。得名于 Saul Kripke 的 K,只向经典命题逻辑公理体系增加了如下规则:
- 必然性规则: 如果 p 是 K 的定理 ,则
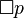 也是。
也是。 - 分配律公理: 如果
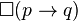 则
则 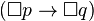 (这也叫做公理 K)
(这也叫做公理 K)
但 K 是一个弱模态逻辑。特别是留下了一个公开的问题,命题是必然的但只偶尔是必然的。如果 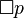 为真则
为真则  为真不是 K 的定理,它是说,必然的真理必然是必然的。这可能不是 K 的大缺陷,因为这些好像是十分奇怪的问题,而试图解答它们的任何尝试都把我们卷入混乱的难题中。无论如何,对这种问题的不同解决方式生成了不同的模态逻辑系统。
为真不是 K 的定理,它是说,必然的真理必然是必然的。这可能不是 K 的大缺陷,因为这些好像是十分奇怪的问题,而试图解答它们的任何尝试都把我们卷入混乱的难题中。无论如何,对这种问题的不同解决方式生成了不同的模态逻辑系统。
这些规则缺乏从 p 的必然性到 p 的实际情况的公理,所以通常要补充上下列“自反性”公理,这就生成经常叫做 T 的一个系统。
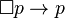 (如果 p 是必然的,则 p 是事实)
(如果 p 是必然的,则 p 是事实)
这是多数但不是全部模态逻辑系统的规则。Jay Zeman 的书《Modal Logic》覆盖了没有这个规则的系统如 S1^0。
其他周知的基本公理:
- 4 :

- B :

- D :

- E :
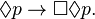
这些公理产生的系统:
- K := K + N
- T := K + T
- S4 := T + 4
- S5 := S4 + B 或 T + E
- D := K + D .
K 到 S5 形成了嵌套的系统层级,建造了正规模态逻辑 的核心。D 重要对探索模态逻辑的道义 解释的人有价值。
今天最常见的系统是模态逻辑 S5 , 它通过增加使所有模态真理是必然的公理来粗壮的解答了这个问题: 例如,如果 p 是可能的,则 p 必然是可能的,如果 p 是必然的,则它必然是必然的。很多人认为它正当的根据是,它是在我们需要每个可能的世界相对于每个其他世界都是可能的时候所获得的系统。不过,模态逻辑的 其他系统已经被公式化了,部分的因为 S5 不能很好的适合我们感兴趣的所有种类的形而上学模态。(若此则意味着可能的世界的谈论不能很好的适合这些种类的模态)。
模态逻辑的发展
尽管亚里士多德 的逻辑几乎全部都关注直言三段论 的理论,他的著作还包含在模态逻辑要点上的一些延伸讨论(比如他著名的在解释篇 § 9 中海战悖论 ),并且它们与潜在性和时间有关连。遵从他的著作,经院学者 为模态逻辑的严格理论开发出了根基,大多在关于本质性 和偶然性 的陈述的逻辑的注释的上下文中。在中世纪的作家中,在 William of Ockham 和 John Duns Scotus 的著作中找到了关于模态逻辑的一些最重要的工作。
形式模态逻辑的缔造者是 C. I. Lewis ,他在专著《A Survey of Symbolic Logic》(1918) 中介入了一个系统(后来叫做 S3),并(同 C. H. Langford 一起)在书《Symbolic Logic》(1932)中介入了系统 S1-S5。J. C. C. McKinsey 在 1941 年使用代数方法(带有算子的布尔代数)来证明 Lewis 的 S2 和 S4 的可判定性。Saul Kripke 从 1959 年开始为模态逻辑设计了关系语义 或可能世界语义 。Vaughan Pratt 在 1976 年介入了动态逻辑 。Amir Pnueli 在 1977 年提出使用时态逻辑来公式化频繁操作并发程序的行为。
时间逻辑 ,在 1957 年由 A. N. Prior 发明,与模态逻辑有密切的关联,因为增加了模态算子 [F] 和 [P],分别意味着今后 和至今 ,导致了时间逻辑的一个系统。时间逻辑的风味包括: 命题动态逻辑(PDL),命题线性时间逻辑(PLTL),线性时间逻辑 (LTL),计算树逻辑 (CTL),Hennessy-Milner 逻辑和 T。
模态逻辑的数学结构,也就是扩充一元运算 的布尔代数 (经常叫做“模态代数 ”),开始出现于 J. C. C. McKinsey 在 1941 年对 S2 和 S4 是可判定性的证明,并于阿尔弗雷德·塔斯基 和他的学生 Bjarni Jonsson 的工作(Jonsson 与 Tarski 1951-52) 中得到完全能力。这项工作显示了 S4 和 S5 是内部代数 的模型,它是最初设计用来捕获拓扑学 的内部算子 和闭包算子 的性质的布尔代数的真扩展 。关于模态逻辑的课本典型不太多提及它与布尔代数 和拓扑学 研究的联系。形式模态逻辑与有关数学的历史概述可参见Goldblatt (2006) 。
引用
- M. Fitting and R.L. Mendelsohn (1998) First Order Modal Logic . Kluwer Academic Publishers.
- James Garson (2003) Modal logic . Entry in the Stanford Encyclopedia of Philosophy .
- Rod Girle (2000) Modal Logics and Philosophy . Acumen (UK). The proof theory employs refutation trees (semantic tableaux). A good introduction to the varied interpretations of modal logic.
- Robert Goldblatt (1992) "Logics of Time and Computation", CSLI Lecture Notes No. 7, Centre for the Study of Language and Information, Stanford University, 2nd ed. (distributed by University of Chicago Press).
- Robert Goldblatt (1993) "Mathematics of Modality", CSLI Lecture Notes No. 43, Centre for the Study of Language and Information, Stanford University. (distributed by University of Chicago Press).
- G.E. Hughes and M.J. Cresswell (1968) An Introduction to Modal Logic , Methuen.
- G.E. Hughes and M.J. Cresswell (1984) A Companion to Modal Logic , Medhuen.
- G.E. Hughes and M.J. Cresswell (1996) A New Introduction to Modal Logic , Routledge.
- E.J. Lemmon (with Dana Scott), 1977, An Introduction to Modal Logic , American Philosophical Quarterly Monograph Series, no. 11 (ed. by Krister Segerberg), Basil Blackwell, Oxford.
- J. Jay Zeeman (1973) Modal Logic . D. Reidel Publishing Company.
参见
外部链接
- A discussion of modal logic by John McCarthy
- Bibliography of Non-Standard Logics by Peter Suber
- List of Logic Systems List of most of the more popular modal logics.
- Advances in Modal Logic (bi-annual international conference and book series in Modal Logic)
致谢
本文包含最初来自Free On-line Dictionary of Computing 的一些材料,经过授权 在 GFDL 下。









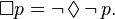

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








