》树:n个结点的有限集。常用操作是遍历,是一种典型的非线性数据结构,具有一对多的关系。
-在非空树中:有且仅有一个根节点(Root);当n>1时,其余结点可以分为m个(m>0)互不相交的有限集T1,T2,...,Tm,其中Ti为根的子树。树中不可以有回路。
-结点:树中的一个数据元素及指向其子树的分支。
-结点的度:结点拥有的子树数。
-叶子结点:度为0的结点。
-分支结点:度不为0的结点。
-树的度:树内各结点的度的最大值。
-子结点(孩子结点):结点的子树的根。
-父节点(双亲结点):B 结点是A 结点的子结点,则A结点是B 结点的父结点。
-兄弟结点:同一父结点的结点。
-堂兄结点:同一层上的结点(父结点不同)。
-祖先结点: 从根到该结点的所经分支上的所有结点。
-子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙。
-树的度:树内各结点的度的最大值。
-有序树:子树有序的树。
-无序树:不考虑子树的顺序。
-层次(深度):根结点的层定义为1,根的孩子为第2层结点,依此类推。
-一棵含有n个结点的K叉树,可能达到的最大深度为n,最小深度为2。
-ADT Tree{
数据对象D:D是具有相同特性的数据元素的集合。
数据关系R:具有一对多的关系。
基本操作:
InitTree(&T); //初始化树
CreateTree(&T); //创建树
ClearTree(&T); //清除树
TreeEmpty(T); //判空
DestoryTree(&T); //销毁树
。。。
}//ADT Tree
》二叉树:每个结点至多有两棵子树(即度小于等于2),子树有左右之分。
-在二叉树的第i层上至多有2i-1个结点(i≥1)。
-深度为k的二叉树至多有2k-1个结点(k≥1)。
-对任何一棵二叉树,度为0的结点总比度为2的结点多一个。
-满二叉树:一棵深度为k且有2k-1个结点的二叉树。
-完全二叉树:设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
-完全二叉树的叶子结点个数:总数为偶数n/2、总数为奇数(n-1)/2+1。
-对一棵有n个结点的完全二叉树(其深度为log2n+1层,每层从左到右),则对任一结点i(1≤i≤n),有:
(1)如果i=1,则结点i是二叉树的根,无双亲;若i>1,则其双亲parent(i)是结点i/2。
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子LCHILD(i)是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子RCHILD(i)是结点2i+1。
ADT BinaryTree{
数据对象D:D是具有相同特性的数据元素的集合。
数据关系R:
-若D为空集,则为空二叉树。
-若D不为空集,则R={H},H是如下二元关系:
在D中存在唯一点根结点root,它在关系H下无前驱;若D-{root}≠ Ø ,则存在D-{root}={Dl,Dr},且Dl∩Dr= Ø 若Dl≠Ø,则Dl中存在唯一的元素xl,<root,xl>∈H,且存在Dl上的关系Hl;若Dr≠Ø,则Dr中存在唯一的元素xr,<root,xr>∈H,且存在Dr上的关系Hr。
-(Dl,{Hl})是一棵符合本定义的二叉树,为根的左子树。
-(Dr,{Hr})是一棵符合本定义的二叉树,为根的右子树。
基本操作:
}//BinaryTree
》二叉树的存储结构
-顺序存储(通过使用数组):将完全二叉树上编号为i的结点元素存储在一维数组下标为i-1的分量中。
-如果树不是完全二叉树,首先需要把它补充成完全二叉树,缺少的地方在数组中空出来。
#define MAX_TREE_SIZE 100;
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;
-链式存储:每一个结点有两个指针域(一个指向左子树,一个指向右子树),一个数据域。
-在n个结点的二叉链表中,有n-1个非空指针域,有n+1个空指针域。
typedef struct BiTree{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
基本操作:
CreatBiTree(BiTree &T);//按先序顺序构造一棵二叉树
PreOrderTraverse(BiTree T);//先序遍历二叉树
InOrderTraverse(BiTree T);//中序遍历二叉树
PostOrderTraverse(BiTree T);//后序遍历二叉树
LevelOrderTraverse(BiTree T);//层次遍历二叉树
》二叉树的遍历
-先序(根)遍历:访问根节点,然后先遍历左子树在遍历右子树。根左右。
-中序(根)遍历:先遍历左子树,在访问根结点,最后遍历右子树。左根右。
-后序(根)遍历:先遍历左子树,在遍历右子树,最后访问根节点。左右根。
-层次遍历:从根开始,依次从上往下,从左到右访问每一个结点。
》线索二叉树
-非线性结构的线性化操作:增加两个指针域-分别指向结点的前驱和后继,利用二叉链表的n+1个空链域
-前驱与后继:在二叉树的先序、中序和后序遍历序列中两个相邻的结点互称为前驱与后继。
-线索:指向前驱或后继结点的指针称为线索。
-线索二叉树:加上线索的二叉链表表示的二叉树。
-线索化:对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。
-双向线索链表:添加头结点:lchild域指向二叉树的根节点,rchild域指向遍历时访问的最后结点。
-线索链表的存储结构
typedef enum PointerTag{Link,Thread};
//Link==0;指针 Thread==1;线索
typedef struct BiTreeNode{
TELemType data;
struct BiThrNode *lchild,*rchild; //左右孩子指针
PointerTag LTag,RTag; //左右标志
}BiTreeNode,*BiThrTree;
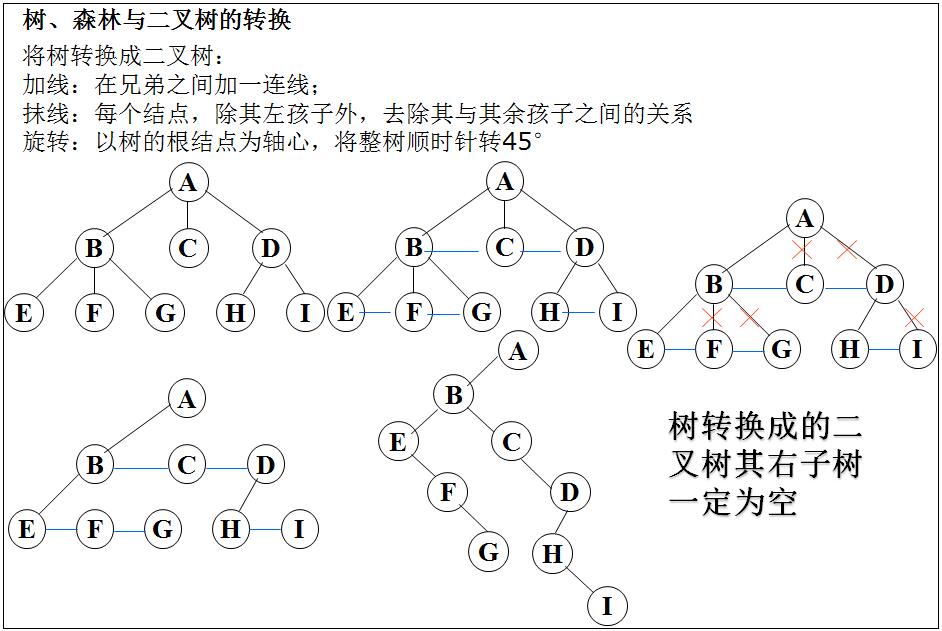
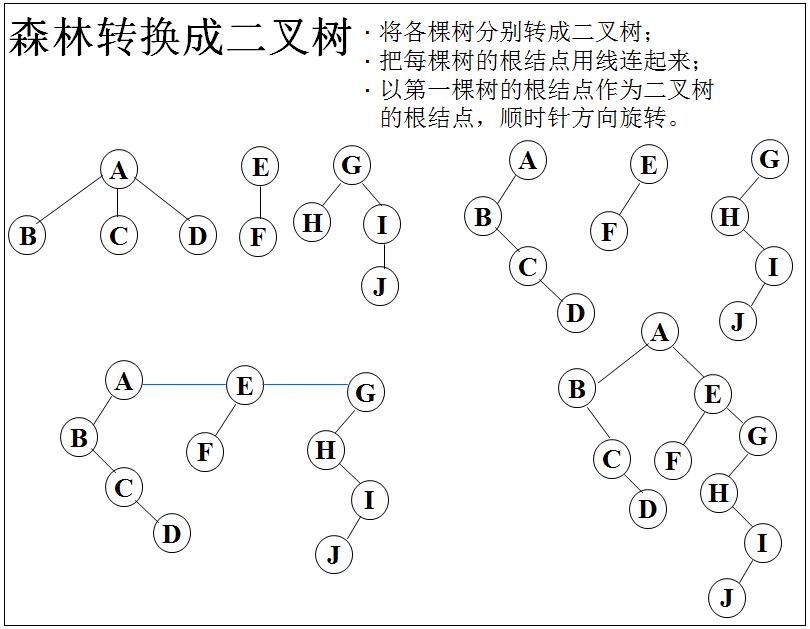
》树和森林
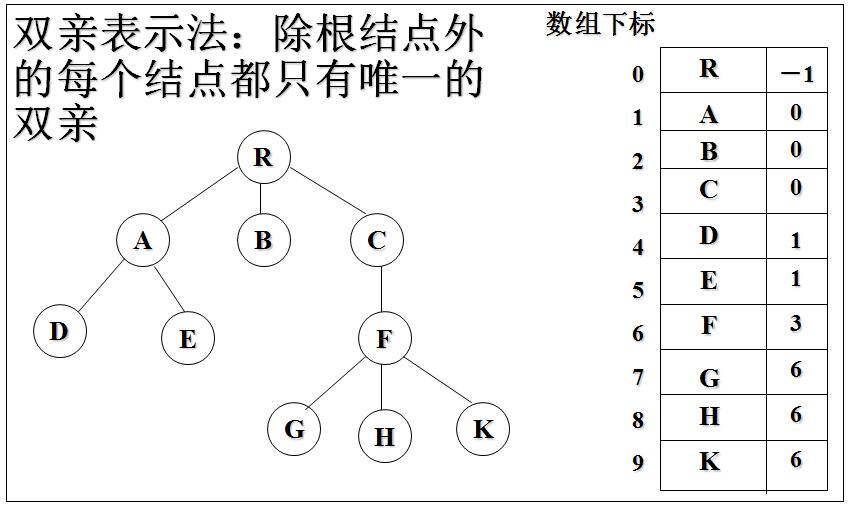
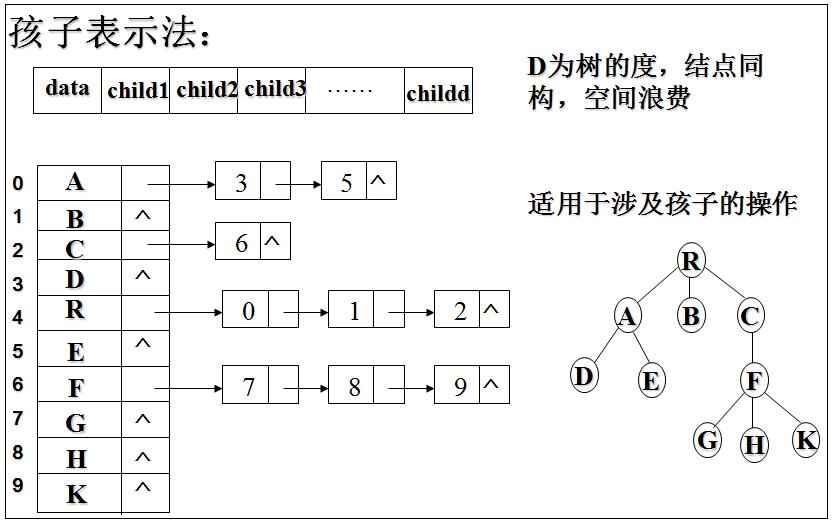
》树的存储结构











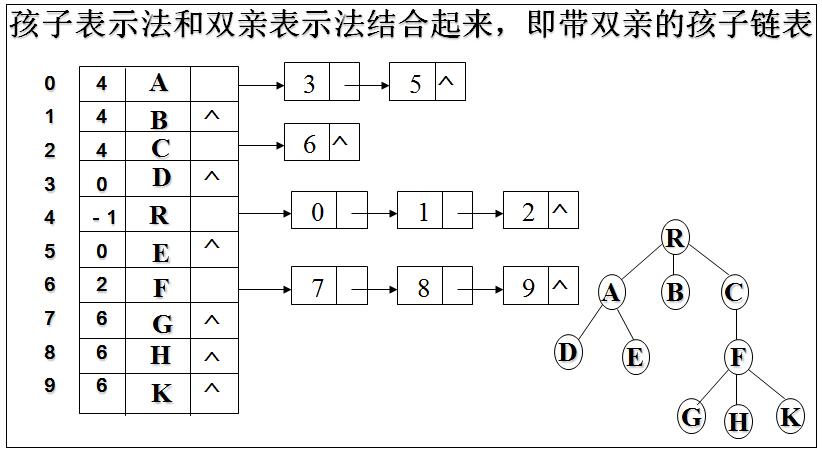













 6169
6169











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








