HDU 5120 Intersection 圆相交 （圆的各类模板）

Time Limit: 4000/4000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 1791    Accepted Submission(s): 686
 

Problem Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.
 

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.
 

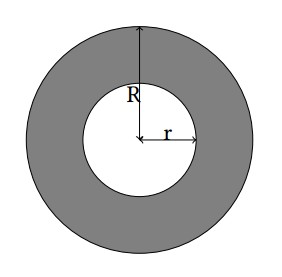
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

Input

The first line contains only one integer T (T ≤ 105), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers xi, yi (0 ≤ xi, yi ≤ 20) indicating the coordinates of the center of each ring.

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

Sample Input

2

2 3

0 0

0 0

2 3

0 0

5 0

 

Sample Output

Case #1: 15.707963

Case #2: 2.250778

题意：给出两个同心的圆环，他们的小圆大圆的半径都一样，只是坐标不相等，之后要求求两个圆环的相交的面积，这个要套用利用到两个圆的相交面积的一个模板，圆环交=大大交-2*大小交+小小交。

#include<iostream>
#include<stdio.h>
#include<queue>
#include<string.h>
#include<algorithm>
#define maxn 1000005
#include<math.h>
#define MS(a,b) memset(a,b,sizeof(a))
#define pi acos(-1.0)
using namespace std;
double cirinter(int x1,int y1,int r1,int x2,int y2,int r2)//圆交面积公式
{
   double d,s,t,a1,a2,s1,s2,s3;
   if(r1<r2){t=r1;r1=r2;r2=t;}
   d=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));//两圆心距离
   if(d>=r1+r2)return 0;//两圆相离
  else if(d<=(r1-r2))//两圆内含
    s=pi*r2*r2;
  else//两圆相交
  {
    a1=acos((r1*r1+d*d-r2*r2)/(2*r1*d));//大圆中扇形圆心角的一半
    a2=acos((r2*r2+d*d-r1*r1)/(2*r2*d));//小圆中扇形圆心角的一半
    s1=a1*r1*r1;//大圆中的那个扇形面积
    s2=a2*r2*r2;//小圆中的那个扇形面积
    s3=r1*sin(a1)*d;//两圆心与两交点组成的四边形面积
    s=s1+s2-s3;//圆交面积
  }
  return s;
}
int main()
{
  int n,i,r,R,x1,y1,x2,y2;
  double area;
  cin>>n;
  for(i=1;i<=n;i++)
  {
      cin>>r>>R;
      cin>>x1>>y1;
      cin>>x2>>y2;
      area=cirinter(x1,y1,R,x2,y2,R)-2*cirinter(x1,y1,R,x2,y2,r)+cirinter(x1,y1,r,x2,y2,r);
      printf("Case #%d: %.6lf\n",i,area);
  }
  return 0;
}