最大子段和

算法设计与分析--求最大子段和问题

问题描述：

给定由n个整数组成的序列(a1,a2, …,an)，求该序列形如

   

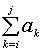
 的子段和的最大值，当所有整数均为负整数时，其最大子段和为0。

多种方式解决：

//最大子段和问题 

#include<stdio.h>
#define N 6

int MaxSum1(int *a,int& besti,int& bestj){//1、三个for循环暴力解决问题 
	int sum=0,max=0;
	for(int i=0;i<N;i++){
		for(int j=i;j<N;j++){
			sum=0; 
			for(int k=i;k<=j;k++){
				sum+=a[k];
			}
			if(max<sum){
				max=sum;
				besti=i;
				bestj=j;
			}
		}
		max=max>=0?max:0;
	}
	return max;
}

int MaxSum2(int *a,int& besti,int& bestj){//1、两个for循环暴力解决问题 
	int sum=0,max=0;
	for(int i=0;i<N;i++){
		sum=0; 
		for(int j=i;j<N;j++){
			sum+=a[j];
			if(max<sum){
				max=sum;
				besti=i;
				bestj=j;
			}
		} 	
		max=max>=0?max:0;
	}
	return max;
}

int MaxSum3(int *a,int left,int right){//分治解决 
	int max=0;
	
	if(left==right){
		if(a[left]>0) 
			max=a[left];
		else
			max=0;
	}else{
		int mid=(left+right)/2;//划分 
		int leftMax=MaxSum3(a,left,mid);
		int rightMax=MaxSum3(a,mid+1,right);
	
		//下面计算中间的
		int max1=0,lefts=0;
		for(int i=mid;i>=left;i--){
			lefts+=a[i];
			if(lefts>max1){
				max1=lefts;
			}
		} 
		int max2=0,rights=0;
		for(int i=mid+1;i<=right;i++){
			rights+=a[i];
			if(rights>max2){
				max2=rights;
			}
		} 
		
		max=max1+max2;
		if(max<leftMax)
			max=leftMax;
		if(max<rightMax)
			max=rightMax;	
	} 
	return max;	
}

int MaxSum4(int* a){ //动态规划解决问题，其实就是判断a[i]之前数的和是否为正数， 
	int max=0;       // 若正数就加上，不是正数则等于当前的数
	int current=0;
	for(int i=0;i<N;i++){
		current=a[i]+(current>0?current:0);     //括号必须加 
		if(current>max)
			max=current;
	} 
	return max;
}

int main()
{
	int a[N]={-2,11,-4,13,-5,-2};
	int max1,max2,max3,max4;
	int besti=0,bestj=0;
		
	max1=MaxSum1(a,besti,bestj);
	printf("三个for循环暴力结果,从%d到%d的子段和最大，为：%d\n",a[besti],a[bestj],max1); 
	
	besti=0;bestj=0;
	max2=MaxSum2(a,besti,bestj);
	printf("两个for循环暴力结果,从%d到%d的子段和最大，为：%d\n",a[besti],a[bestj],max2); 
	
	max3=MaxSum3(a,1,N-1);
	printf("分治解决,子段和最大，为：%d\n",max3); 
	
	max4=MaxSum4(a);
	printf("动态规划解决,子段和最大，为：%d\n",max4); 
	
	return 0;
}