我们知道神经网络有forward propagation,很自然会想那有没有Backpropagation,结果还真有。
forward progation相当于神经网络额一次初始化,但是这个神经网络还缺少训练,而Backpropagation Algorithm就是用来训练神经网络的。
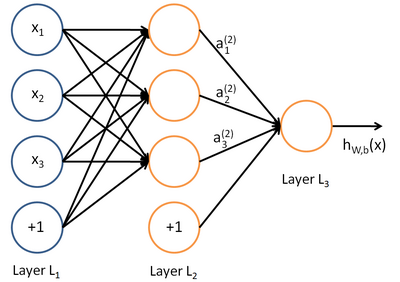
假设现在又m组训练集
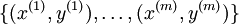
代价函数为:
单个神经元的
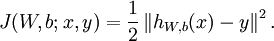
神经网络的:
![\begin{align}J(W,b)&= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \\&= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left\| h_{W,b}(x^{(i)}) - y^{(i)} \right\|^2 \right) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2\end{align}](http://deeplearning.stanford.edu/wiki/images/math/4/5/3/4539f5f00edca977011089b902670513.png)
现在用经典的梯度下降法求解:
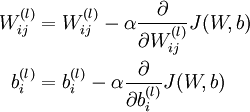
其中
![\begin{align}\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &=\left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)} \\\frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &=\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)})\end{align}](http://deeplearning.stanford.edu/wiki/images/math/9/3/3/93367cceb154c392aa7f3e0f5684a495.png)
我们引入误差项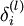 代表第l层的第i个单元对于整个我们整个神经网络输出误差的贡献大小
代表第l层的第i个单元对于整个我们整个神经网络输出误差的贡献大小
还记得我们前面提到
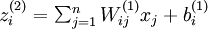
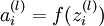
Backpropagation algorithm:
- Perform a feedforward pass, computing the activations for layers L2, L3, and so on up to the output layer
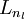 .
. - For each output unit i in layer nl (the output layer), set
-
- For
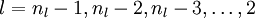
-
For each node
i in layer
l, set
-
-
For each node
i in layer
l, set
- Compute the desired partial derivatives, which are given as:
-
The algorithm can then be written:
- Perform a feedforward pass, computing the activations for layers
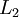 ,
, 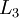 , up to the output layer
, up to the output layer 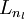 , using the equations defining the forward propagation steps
, using the equations defining the forward propagation steps - For the output layer (layer
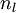 ), set
), set
-
- For
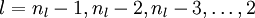
-
Set
-
-
Set
- Compute the desired partial derivatives:
-
还BP算法中很重要的是中间隐层误差项的推导,我们接下来特别地详细研究一下:
我们假设代价函数为
-
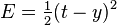 ,
,
其中
-
 是训练集的输出线
是训练集的输出线
-
 是实际的输出项
是实际的输出项
-
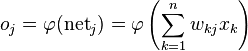
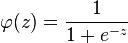
我们现在也求解

其中
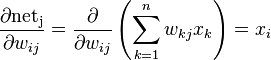


特别地,如果是隐含层j,那么
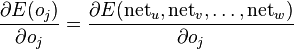
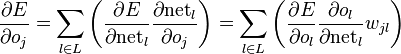
综上可以得到:
参考资料:
http://en.wikipedia.org/wiki/Backpropagation
http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial
版权声明:本文为博主原创文章,未经博主允许不得转载。







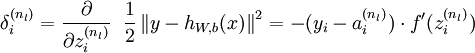
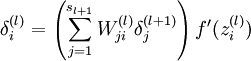
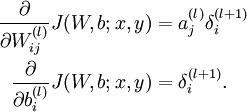
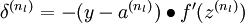
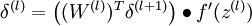
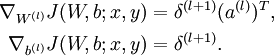
















 2813
2813











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








