平衡二叉树插入操作的原理及实现

在二叉搜索树中我们知道在删除操作中如果一直用一侧的树来代替删除的父节点就会出现一侧子树过高和一侧子树过低，同样，对于一个这样不平衡的树，再进行二叉搜索树的相关操作时就会降低程序的效率。所以平衡二叉树就应需求而生了，他是左右子树高度差不超过1的二叉搜索树，这样就会使树更对称。
关于平衡二叉树的一些概念：
平衡因子（Balance Factor）：
左右子树高度差的绝对值（BF(T) = | hl - hr |）。
平衡二叉树（Balance Binary Tree / AVL树）：
空树或者任一结点的左右子树高度差的绝对值不超过1的二叉搜索树。
根据平衡二叉树的这一特点，显然节点的高度也成为其特性之一，故在插入和删除这种可能会导致平衡因子大于1的情况出现，需要在进行操作时注意不能破坏其特性。故要在二叉搜索树的基础上加一个高度：

typedef struct node *AVL;
struct node{
	ElementType data;
	int height;
	AVL left;
	AVL right;
}

因为涉及到对高度的判断，所以我们先来做一些准备工作：

• 获得节点的高度：

int GetHeight(AVL tree)
{
	if(!tree) return 0;
	return tree->height;
}

• 更新节点高度：

AVL UpdateHeight(AVL tree)
{
	tree->height=max(GetHeight(tree->left),GetHeight(tree->right))+1;
	return tree;
}

• 得到节点的平衡因子：

int GetBT(AVL tree)
{
	int BT=GetHeight(tree->left)-GetHeight(tree->right);//不用绝对值是因为方便判断用哪种方式调整
	return BT;
}

1.插入操作的原理及其调整的函数

（1）右单旋：麻烦节点在发现者的右子节点的右子树上
（至于他为什么叫右单旋全看自己怎么理解了，书上的解释是在右边插入故调整称为右单旋）
我们把发现破坏平衡二叉树平衡的节点称为发现者（也就是第一个平衡因子大于1的节点），把出入的节点（破坏平衡的）成为麻烦节点。

上图的情况节点插入到右子树作为叶子结点使平衡被破坏，而发现者是A，所以我们需要向左旋转（至于他为什么叫右单旋全看自己怎么理解了）恢复平衡，旋转时其实就是对发现者（A）、子节点（B）、麻烦节点所在的分支（B_R）向左旋转，进而再根据二叉搜索树的特性：A<B_L<B，把B_L作为A的右子树。注意：图中A只是代表发现者并不一定是根节点！！！

AVL RR(AVL A)
{
	AVL B=A->right;
	A->right=B->left;
	B->left=A;
	UpdateHeight(A);
	UpdateHeight(B);
	return B;
}

（2）左单旋：麻烦节点在发现者的左子节点的左子树上

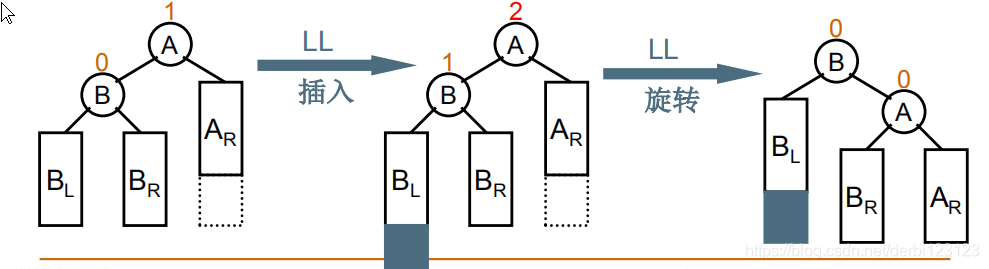
这时要向右旋转，同样我并不理解他为毛叫左单旋，理解的模式和右单旋一样，
向右旋转发现者（A）、左子节点（B）、麻烦节点所在分支（B_L），再根据B<B_R<A让B_R作为A的左子树。注意：图中A只是代表发现者并不一定是根节点！！！

AVL LL(AVL A)
{
	AVL B=A->left;
	A->left=B->right;
	B->right=A;
	UpdateHeight(A);
	UpdateHeight(B);
	return B;
}

上面两种都是比较容易理解的，毕竟插入的节点都在那么清楚的位置上，当插入的节点是树的中部的叶子结点时操作就要涉及树的内部，代码很短但更需自己画图理解。
（3） 左—右双旋：

对于插入到如图两个位置的麻烦节点都适用，显然这时涉及的范围大了，不过万古不变的真理是B<C<C_R<A。我们就是根据这一特性来调整旋转后的节点，根据之前两种情况，我们可以看出只要处理麻烦节点到发现者这条路上的节点即可完成调整，但此时这条路上有四个部分（A、B、C、C_R/C_L），所以我们要旋转两次：先旋转B、C、C_R/C_L，再旋转A、C、C_R/C_L（上面的图只有结果，需要自己画具体的图想，自己去想哪个用左单旋哪个用右单旋）。

AVL LR(AVL A)
{
	A->left=RR(A->left);//旋转B、C、CR/CL
	return LL(A);//旋转A、C、CR/CL
}

（4）右—左单旋：

就是先旋转B、C、C_R/C_L，再旋转A、C、C_R/C_L

AVL RL(AVL A)
{
	A->right=LL(A->right);//旋转B、C、CR/CL
	return RR(A);//旋转A、C、CR/CL
}

2. 插入操作的实现：

终于哔哔完那几种调整函数了，重要的还是自己画图取体会，不说了，直接上代码吧，其实就是在二叉搜索树的插入函数上了判断平衡因子以及进行相应调整的函数。重点在于结合自己画的流程图理解

//插入新节点
AVL Insert(AVL tree,ElementType X)
{
	if(!tree){
		tree=new node;
		tree->data=X;
		tree->left=tree->right=NULL;
	}else if(X<tree->data){
		tree->left=Insert(tree->left,X);
		if(GetBT(tree)==2){//平衡因子超过1，自己想为什么是==2而不是>=2
			if(tree->left->data>X){//左单旋
				tree=LL(tree);
			}else{//左右单旋
				tree=LR(tree);
			}
		}
	}else{
		tree->right=Insert(tree->right,X);
		if(GetBT(tree)==-2){//平衡因子超过1，自己想为什么是==-2而不是<=-2
			if(tree->right->data>X){//右单旋
				tree=RR(tree);
			}else{//右左单旋
				tree=RL(tree);
			}
		}
	}
	return tree;
}