二叉搜索树（BST）

定义

二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：

1. 非空左子树的所有键值小于其根节点的键值。
2. 非空右子树的所有键值大于其根结点的键值。
3. 左、右子树都是二叉搜索树。

---

操作

• 查找元素X
• 找最大值max，最小值min
• 插入元素X
• 删除元素X

/*   二叉搜索树结点定义  */
typedef struct node* bst;
struct node 
{
	int data;
	bst left;
	bst right;
};

1. 查找元素X（非递归）

bst Find(int x, bst t)
{
	while(t)
	{
		if(x > t->data) t = t->right;//往右边移动去找
		else if(x < t->data) t = t->left;//往左边移动去找
		else return t;//找到了，返回地址
	}
	return NULL;//没有找到
}

2. 找最大值 、最小值（非递归）
   最大值一定在树的最右边，最小值一定在树的最左边

bst Findmin(bst t)
{
	if(t)
		while(t->left) t = t->left;
	return t;
}

bst Findmax(bst t)
{
	if(t)
		while(t->right) t = t->right;
	return t;
}

3. 插入元素X

bst Insert(int x, bst t)
{
	if(!t)//如果是空的，就说明找到了插入位置
	{
		t = (bst)malloc(sizeof(struct node));
		t->data = x;
		t->left = t->right = NULL;
	}
	else 
	{
		if(x < t->data)//比它小，就去左边插入
			t->left = Insert( x, t->left);
		else if(x > t->data)//比它大，就去右边插入
			t->right = Insert( x, t->right);
	}
	return t;
}

如上图：比如要插入的是1，此时1应该往3的左边插入，所以3的左儿子的地址就等于下一次递归所生成结点的地址，而这个结点的data就等于被插入元素的值1。

4.删除元素X

考虑三种情况：

• 要删除的是叶节点：直接删除，并修改其父节点指针，置为NULL
  
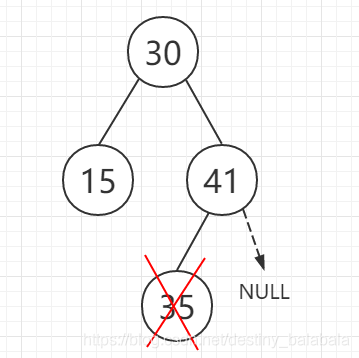
• 要删除结点只有一个孩子结点：将其父节点的指针指向被删除结点的孩子节点
  
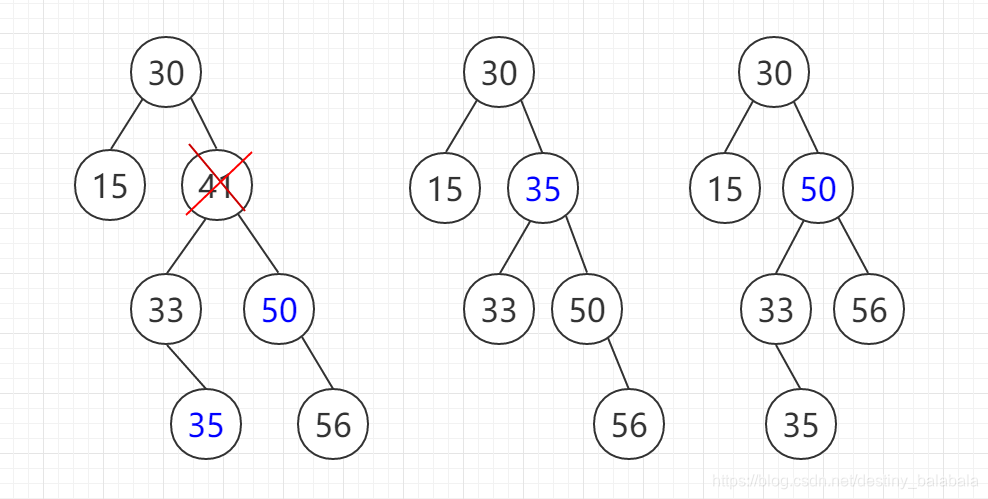
• 要删除的结点有两个孩子结点：用右子树的最小元素或者左子树的最大元素代替被删除元素（因为这样可以保证子树仍然是BST的结构）
  

bst Delete(int x, bst t)
{
	bst temp;
	if(!t) printf("要删除元素未找到!\n");
	//首先是一个查找过程
	else if(x < t->data)
		t->left = Delete( x, t->left);
	else if(x > t->data)
		t->right = Delete( x, t->right);
	else//找到了
		if(t->left && t->right)//有两个孩子节点
		{
			temp = Findmin(t->right);
			t->data = temp->data;
			t->right = Delete( t->data, t->right);//去右边删除最小元素
		}
		else//只有一个孩子结点或者没有
		{	
			temp = t;
			if(!t->left)//有右孩子或者无孩子
				t = t->right;//把指向它的指针置为指向它的右儿子或空
			else if(!t->right)//有左孩子或者无孩子
				t = t->left;//把指向它的指针置为指向它的左儿子或空
			free(temp);
		}
	return t;
}