什么是信息?
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。
信息量的度量:
一般情况,我们用概率的倒数的对数函数来表示某一个事件(某一个符号)出现所带来的信息量。
每个符号的自信息量: ,单位是bit
信息熵:每个信息量的数学期望 : ,就是其概率对应的相乘相加!!
别急,你可能只是从数学公式上,看到信息熵怎么得来的,现在,我想用一个例子更好的引入信息熵。
信息熵的引入
直觉上,信息量等于传输该信息所用的代价,这个也是通信中考虑最多的问题。比如说:赌马比赛里,有4匹马,获胜概率分别为
。
接下来,让我们将哪一匹马获胜视为一个随机变量 。假定我们需要用尽可能少的二元问题来确定随机变量
的取值。
例如:问题1:A获胜了吗?问题2:B获胜了吗?问题3:C获胜了吗?最后我们可以通过最多3个二元问题,来确定 的取值,即哪一匹马赢了比赛。
如果 X=A ,那么需要问1次(问题1:是不是A?),概率为 ;
如果 X=B ,那么需要问2次(问题1:是不是A?问题2:是不是B?),概率为 ;
如果 X=C ,那么需要问3次(问题1,问题2,问题3),概率为 ;
如果 X=D ,那么同样需要问3次(问题1,问题2,问题3),概率为;
那么很容易计算,在这种问法下,为确定 X 取值的二元问题数量为:
那么我们回到信息熵的定义,会发现通过之前的信息熵公式,神奇地得到了:
在二进制计算机中,一个比特为0或1,其实就代表了一个二元问题的回答。也就是说,在计算机中,我们给哪一匹马夺冠这个事件进行编码,所需要的平均码长为1.75个比特。
平均码长的定义为:
很显然,为了尽可能减少码长,我们要给发生概率 较大的事件,分配较短的码长
。这个问题深入讨论,可以得出霍夫曼编码的概念。
那么 四个实践,可以分别由
表示,那么很显然,我们要把最短的码0 分配给发生概率最高的事件 A ,以此类推。而且得到的平均码长为1.75比特。如果我们硬要反其道而行之,给事件A 分配最长的码111 ,那么平均码长就会变成2.625比特。
霍夫曼编码就是利用了这种大概率事件分配短码的思想,而且可以证明这种编码方式是最优的。我们可以证明上述现象:
为了获得信息熵为 H(X) 的随机变量X 的一个样本,平均需要抛掷均匀硬币(或二元问题)H(X) 次(参考猜赛马问题的案例)
信息熵是数据压缩的一个临界值(参考码长部分的案例)。
这可能是信息熵在实际工程中,信息熵最最重要且常见的一个用处。
信息熵:
信息熵的定义与上述这个热力学的熵,虽然不是一个东西,但是有一定的联系。熵在信息论中代表随机变量不确定度的度量。一个离散型随机变量 的熵
定义为:
信息理论的鼻祖之一Claude E. Shannon把信息(熵)定义为离散随机事件的出现概率。
所谓信息熵,是一个数学上颇为抽象的概念,在这里不妨把信息熵理解成某种特定信息的出现概率。
一般而言,当一种信息出现概率更高的时候,表明它被传播得更广泛,或者说,被引用的程度更高。我们可以认为,从信息传播的角度来看,信息熵可以表示信息的价值。这样子我们就有一个衡量信息价值高低的标准,可以做出关于知识流通问题的更多推论。
信息论之父克劳德·香农,总结出了信息熵的三条性质:
①非负性:即收到一个信源符号所获得的信息量应为正值,H(U)≥0
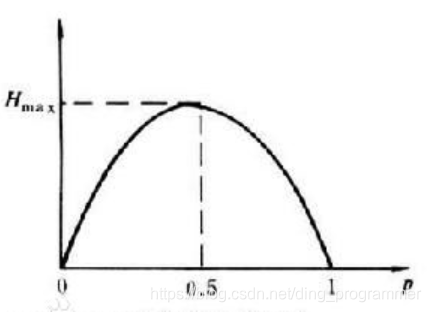
②对称性:即对称于P=0.5
③确定性:H(1,0)=0,即P=0或P=1已是确定状态,所得信息量为零
④极值性:因H(U)是P的上凸函数,且一阶导数在P=0.5时等于0,所以当P=0.5时,H(U)最大。
事件,如果同时发生,且相互独立,则可以得出:
那么信息熵为
补充一下,如果两个事件不相互独立,那么满足:
,其中
是互信息(mutual information),代表一个随机变量包含另一个随机变量信息量的度量,这个概念在通信中用处很大。
比如一个点到点通信系统中,发送端信号为 ,通过信道后,接收端接收到的信号为
,那么信息通过信道传递的信息量就是互信息
。根据这个概念,香农推出了一个十分伟大的公式,香农公式,给出了临界通信传输速率的值,即信道容量:
参考文献:
https://blog.csdn.net/qq_39521554/article/details/79078917








 本文介绍了信息及信息熵的概念,通过赌马比赛的例子引入信息熵,说明了其与平均码长的关系,引出霍夫曼编码。还阐述了信息熵是数据压缩的临界值,介绍了信息熵的性质,提及互信息和香农公式,给出了临界通信传输速率的值。
本文介绍了信息及信息熵的概念,通过赌马比赛的例子引入信息熵,说明了其与平均码长的关系,引出霍夫曼编码。还阐述了信息熵是数据压缩的临界值,介绍了信息熵的性质,提及互信息和香农公式,给出了临界通信传输速率的值。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








