Coursera机器学习-第四周-Neural Network ForwardPropagation

Neural NetWork的由来

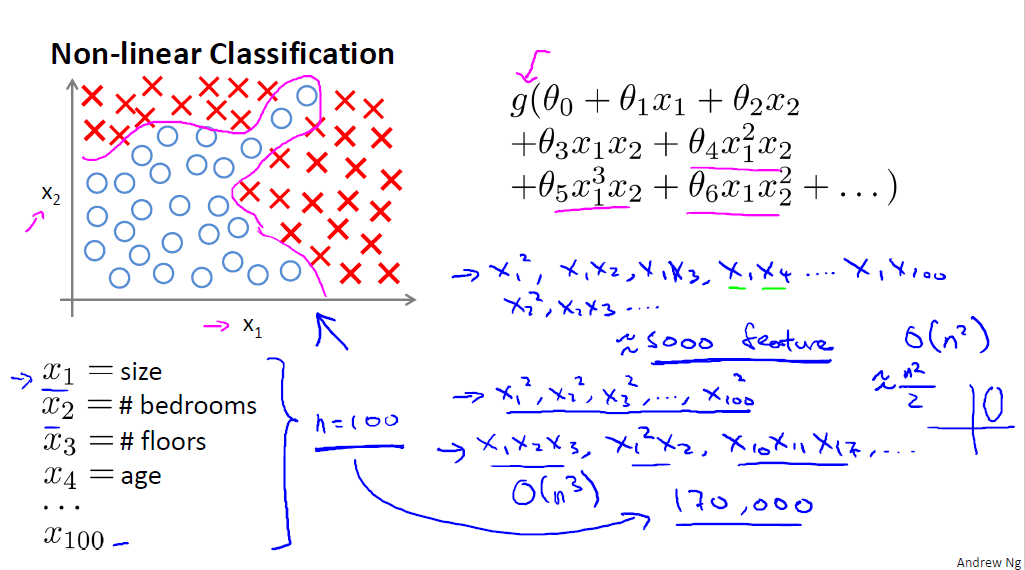
先考虑一个非线性分类，当特征数很少时，逻辑回归就可以完成了，但是当特征数变大时，高阶项将呈指数性增长，复杂度可想而知。如下图：对房屋进行高低档的分类，当特征值只有$x_1,x_2,x_3$时，我们可以对它进行处理，分类。但是当特征数增长为$x_1,x_2....x_100$时，分类器的效率就会很低了。
这里的$g(z)=1/(1+e^{-z})$

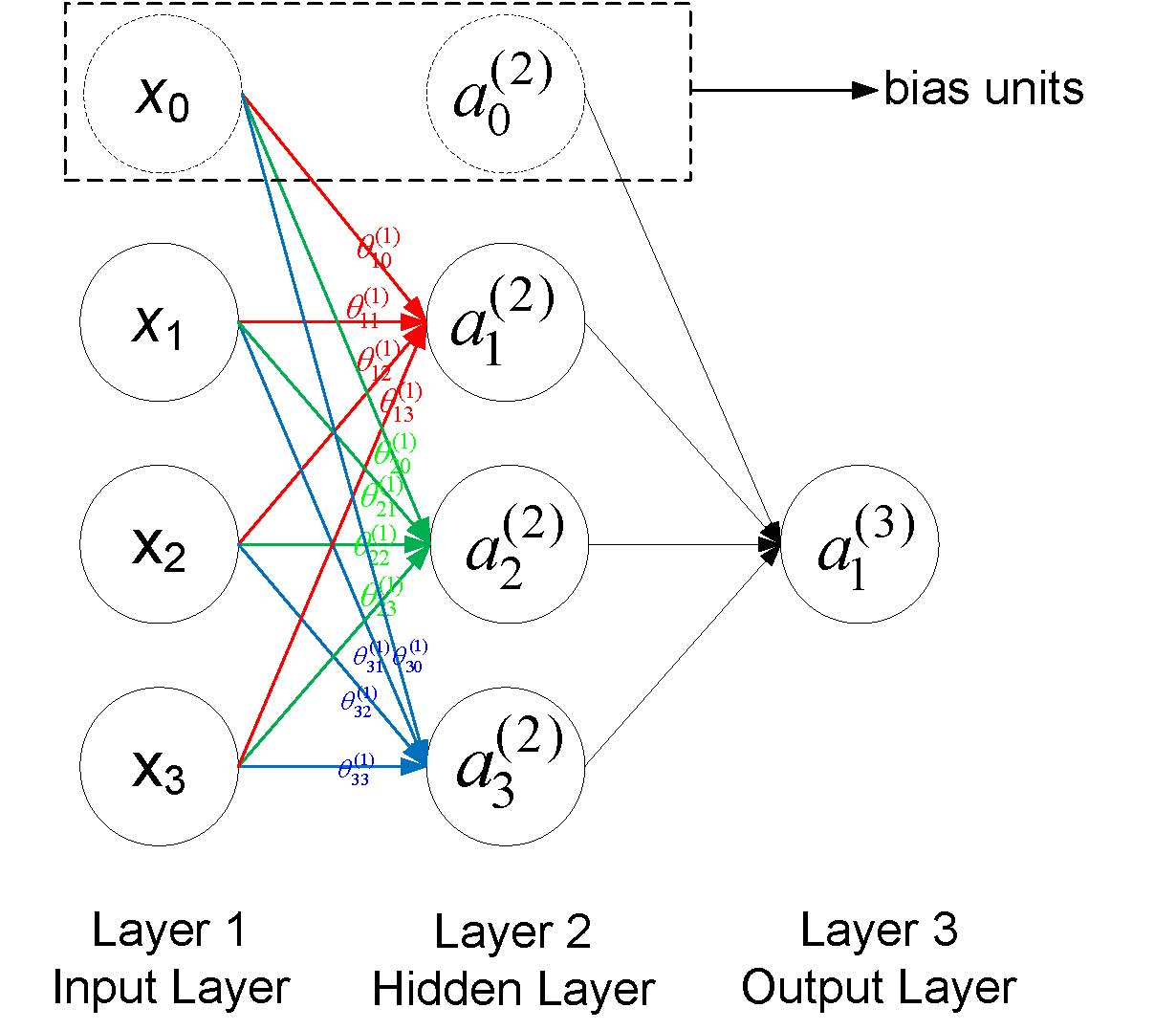
符号说明：

• $a_i^{(j)}$表示第j层网络的第i个神经元，例如下图$a_1^{(2)}$就表示第二层的第一个神经元
• $\theta^{(j)}$表示从第$j$层到第$j+1$层的权重矩阵，例如下图所有的$\theta^{(1)}$表示从第一层到第二层的权重矩阵
• $\theta^{(j)}_{uv}$表示从第j层的第v个神经元到第j+1层的第u个神经的权重，例如下图中$\theta^{(1)}_{23}$表示从第一层的第3个神经元到第二层的第2个神经元的权重，需要注意到的是下标uv是指v->u的权重而不是u->v，下图也给出了第一层到第二层的所有权重标注
• 一般地，如果第j层有$s_j$个神经元（不包括bias神经元），第j+1层有$s_{j+1}$个神经元（也不包括bias神经元），那么权重矩阵$\theta^{j}$的维度是$(s_{j+1}\times( s_j+1))$

Forward propagation

第一层，称之为input Layer $x=\{x_1,x_2,x_3\}$
第二层至最后一层，成为hidden layers: $a_2^{(2)},a_1^{(2)},a_3^{(2)}$
最后一层是output layer: $h_\theta(x)$
通俗点说，向前传播就是上层处理完的数据作为你的输入数据，然后进行处理(权重)，再传给下一层，这样逐层处理，最后输出。

a(2)1=g(θ(1)10x0+θ(1)11x1+θ(1)12x2+θ(1)13x3)