LeetCode 叶子相似的树

题目

  请考虑一颗二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

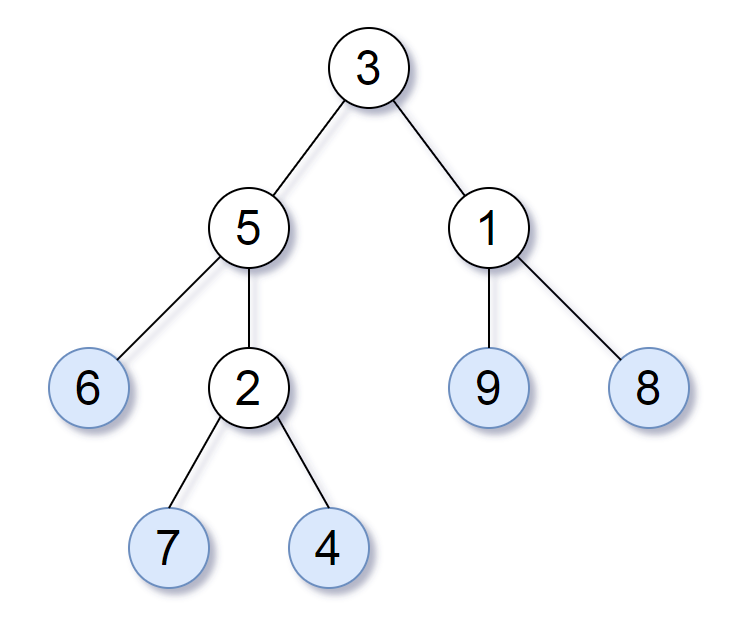
  举个例子，如上图所示，给定一颗叶值序列为 (6, 7, 4, 9, 8) 的树。如果有两颗二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。如果给定的两个头结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

解法

---

一、深度优先搜索-先序遍历( Python )

class Solution:
    def leafSimilar(self, root1: TreeNode, root2: TreeNode) -> bool:
        
        def pre_order(node, leafs):
            if node:
                if not(node.left or node.right):
                    leafs.append(node.val)
                pre_order(node.left, leafs)
                pre_order(node.right, leafs)
                
        leafs1, leafs2 = [], []
        pre_order(root1, leafs1)
        pre_order(root2, leafs2)
        return leafs1 == leafs2

基本思路

  通过先序遍历将找到所有叶子节点并将其放入列表中，该操作分别对root1和root2各执行一次即可。

复杂度分析

  时间复杂度为$O\left(N_1+N_2\right)$，空间复杂度为$O\left(N_1+N_2+H_1+H_2\right)$，其中$N_1,N_2$分别表示两棵树的节点数，$H_1,H_2$分别表示两棵树的高度。

二、迭代-先序遍历( Python )

class Solution:
    def leafSimilar(self, root1: TreeNode, root2: TreeNode) -> bool:
        return self.iterative(root1) == self.iterative(root2)
        
    def iterative(self, root):
        res, stack = [], []
        while stack or root:
            if root:
                stack.append(root)
                root = root.left
            else:
                root = stack.pop()
                if not (root.left or root.right):
                    res.append(root.val)
                root = root.right
        return res

基本思路

  只不过是把递归换成迭代而已，其他思路不变。

复杂度分析

  时间复杂度为$O\left(N_1+N_2\right)$，空间复杂度为 O ( max ⁡ { N 1 , N 2 } ) O \left( \max \left\{N_1,N_2 \right\} \right) O(max{N1​,N2​})。