不止是链：静态链表与循环链表的内存魔法

原创于 2025-11-06 01:02:07 发布 · 437 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #数据结构

数据结构杂谈专栏收录该内容

4 篇文章

订阅专栏

王者杯·14天创作挑战营·第7期 10w+人浏览 107人参与

引言：数据结构的“因地制宜”

一、静态链表的核心思想：游标（Cursor）

二、静态链表的初始化：构建“备用链表”

三、静态链表的插入操作：巧借“备用链表”之力

1. 分配空间 (Malloc_SSL)

2. 插入元素 (ListInsert)

四、静态链表的删除操作：回收空间，重归“备用链表”

六、从静态链表到循环链表：解决“单行道”的烦恼

引言：数据结构的“因地制宜”

在数据结构的学习中，我们常常会陷入一个误区：认为线性表的顺序存储（数组）和链式存储（链表）孰优孰劣。事实上，不能简单地说哪个好，哪个不好，需要根据实际情况，来综合平衡采用哪种数据结构更能满足和达到需求和性能。这种务实的思想，正是我们今天要探讨的主角——静态链表——诞生的初衷。

静态链表，是一种巧妙地用数组模拟链表结构的数据结构。它的出现，完美解决了早期高级语言（如 Basic、Fortran）因缺乏指针机制而无法实现传统链表的困境。它并非一种“退而求其次”的妥协，而是一种充满智慧的“曲线救国”方案，让我们得以在受限的环境中，依然享受链表灵活插入删除的优势。

一、静态链表的核心思想：游标（Cursor）

静态链表的核心在于一个概念：游标（Cursor）。

在传统的单链表中，每个节点包含两个部分：data（数据域）和 next（指针域），next 指向下一个节点的内存地址。而在静态链表中，由于没有指针，我们用一个整型变量 cur 来代替 next。这个 cur 存储的不是内存地址，而是下一个节点在数组中的下标。

因此，静态链表的每一个元素（数组的一个单元）都由两个域组成：

data: 存放实际的数据元素。
cur: 存放后继元素在数组中的下标，我们称之为“游标”。

这种用数组描述链表的方法，也被称为“游标实现法”。它让数组拥有了链表的“灵魂”，即通过逻辑上的链接关系来组织数据，而非物理上的连续存储。

为了方便操作，我们通常会将数组建立得比实际需要大一些，预留出空闲空间，以便于后续的插入操作不至于溢出。

#define MAXSIZE 1000    /*存储空间的初始分配量*/
/* 线性表之静态链表存储结构 */

typedef struct
{
   ElemType data ;
   int cur ;    /* 游标 为0时表示无指向 */
 } Component, StaticLinkList(MAXSIZE);

另外我们对这个数组的第一个和最后一个元素作为特殊元素处理，不存数据，我们称之为备用链表。

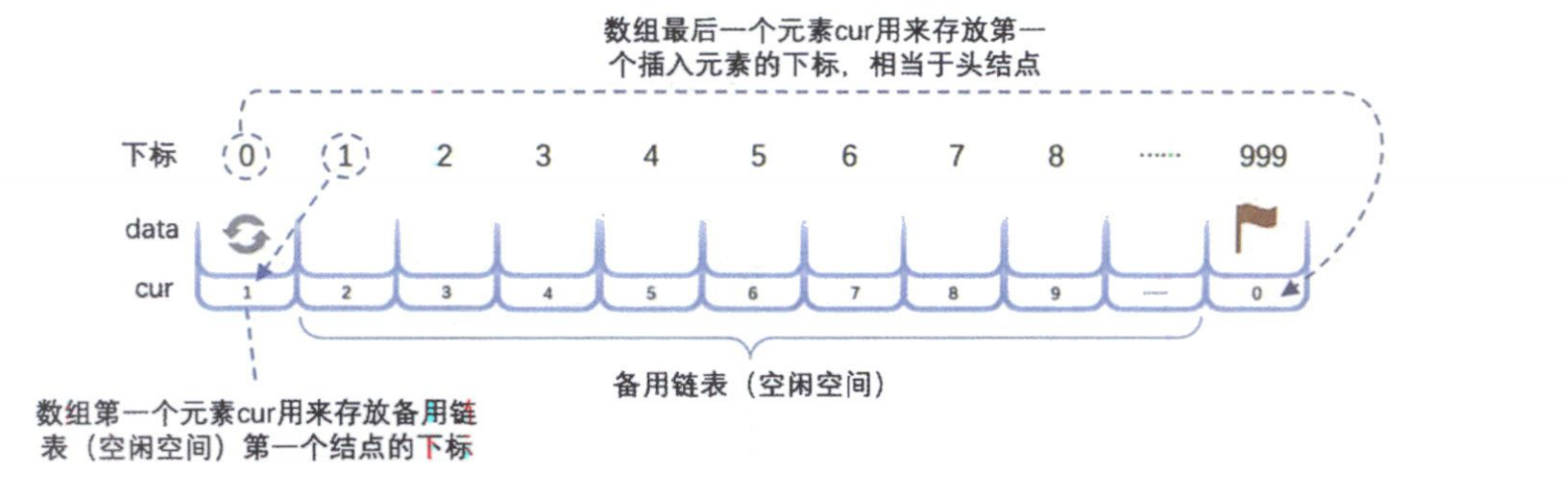
二、静态链表的初始化：构建“备用链表”

静态链表的初始化是其独特之处。我们不直接使用整个数组，而是将数组的第一个元素（下标为0）和最后一个元素（下标为 MAXSIZE-1）作为特殊元素处理。

数组第一个元素 (下标0): 它的 cur 域被用来存放“备用链表”的第一个结点的下标。所谓备用链表，就是所有未被使用的、空闲的数组单元组成的链表。
数组最后一个元素 (下标 MAXSIZE-1): 它的 cur 域则存放“头结点”的下标，也就是第一个有实际数据的元素的下标。当整个链表为空时，此值为0。

初始代码如下：

#define MAXSIZE 1000

typedef struct {
    ElementType data;
    int cur; // 游标，为0时表示无指向
} Component, StaticLinkList[MAXSIZE];

Status InitList(StaticLinkList space) {
    int i;
    for (i = 0; i < MAXSIZE - 1; i++) {
        space[i].cur = i + 1; // 将所有元素串成备用链表
    }
    space[MAXSIZE - 1].cur = 0; // 最后一个元素的cur置为0，表示链表为空
    return OK;
}

此时，数组的状态如下图所示：

下标0的 cur 指向1（备用链表的第一个空闲位置）。
下标1的 cur 指向2，下标2的 cur 指向3...以此类推，直到下标998的 cur 指向999。
下标999的 cur 为0，表示这是备用链表的末尾。

三、静态链表的插入操作：巧借“备用链表”之力

在静态链表中，插入操作不再像顺序表那样需要移动大量元素，而是通过修改游标来实现。其关键在于如何模拟 malloc() 和 free() 函数的功能。

1. 分配空间 (`Malloc_SSL`)

我们首先需要实现一个函数 Malloc_SSL，用于从“备用链表”中获取一个空闲的数组单元。

int Malloc_SSL(StaticLinkList space) {
    int i = space[0].cur; // 获取备用链表的第一个结点下标
    if (space[0].cur) { // 如果备用链表非空
        space[0].cur = space[i].cur; // 将备用链表的头指针指向下一个空闲结点
    }
    return i; // 返回分配到的下标
}

这个函数的作用就是返回一个可用的下标。例如，在初始化后的状态下，第一次调用 Malloc_SSL 会返回7（假设当前链表已存入“甲乙丁戊己庚”，如图所示），因为下标7是备用链表的第一个空闲位置。

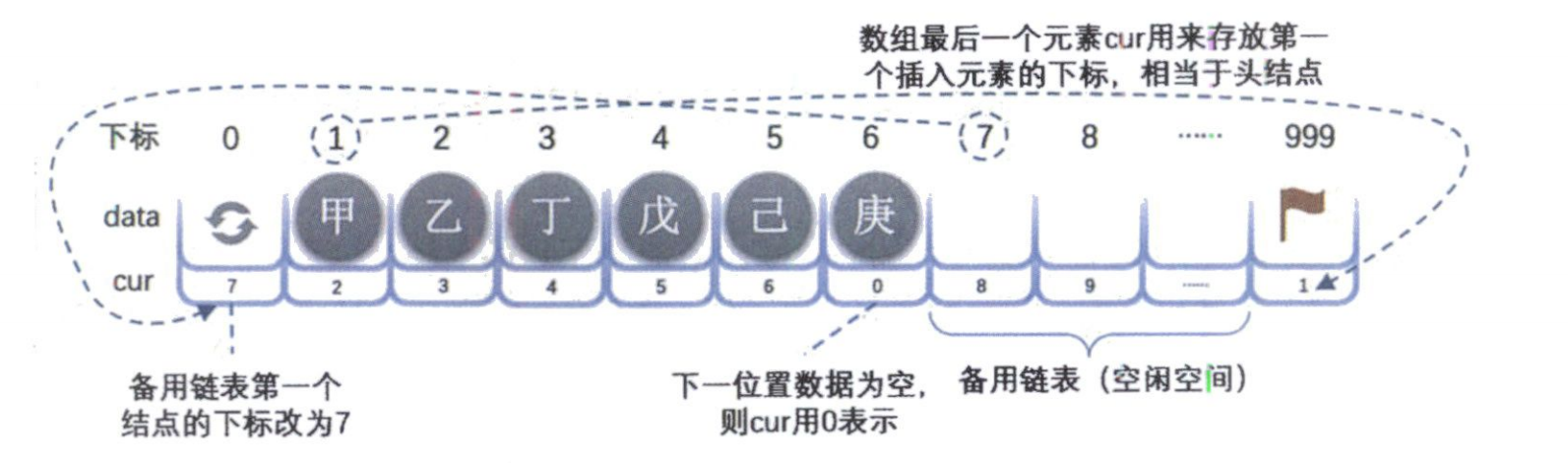
2. 插入元素 (`ListInsert`)

现在，假设我们要在“乙”和“丁”之间插入一个新元素“丙”。我们无需移动任何元素，只需修改几个游标即可。

Status ListInsert(StaticLinkList L, int i, ElementType e) {
    int j, k, l;
    k = MAXSIZE - 1; // k初始为最后一个元素的下标
    if (i < 1 || i > ListLength(L) + 1) {
        return ERROR;
    }

    j = Malloc_SSL(L); // 从备用链表中获取一个空闲位置，比如下标7
    if (j) {
        L[j].data = e; // 将数据赋给新分配的位置

        // 找到第i个元素之前的位置
        for (l = 1; l <= i - 1; l++) {
            k = L[k].cur; // k不断向前移动，最终指向第i-1个元素
        }

        // 将新元素的游标指向原第i个元素
        L[j].cur = L[k].cur;
        // 将第i-1个元素的游标指向新元素
        L[k].cur = j;

        return OK;
    }
    return ERROR;
}

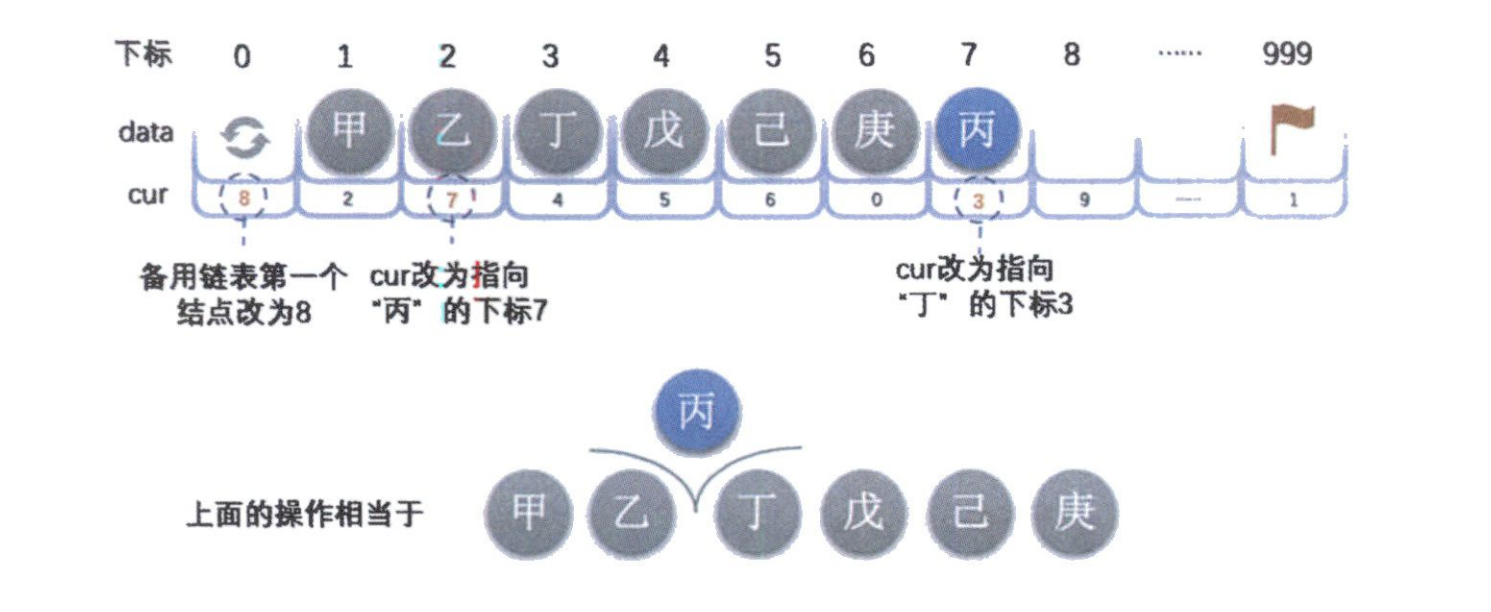
执行过程详解：

调用 Malloc_SSL(L)，获得空闲下标 j=7。
将数据 e（“丙”）存入 L[7]。
通过循环找到第 i-1 个元素（即“乙”）的位置，其下标为 k=2。
修改游标：L[7].cur = L[2].cur （即 L[7].cur = 3），让“丙”指向“丁”。
修改游标：L[2].cur = 7，让“乙”指向“丙”。

至此，插入完成！整个过程仅修改了三个游标，时间复杂度为 O(n)，但避免了数据的物理移动，效率远高于顺序表。

四、静态链表的删除操作：回收空间，重归“备用链表”

删除操作同样优雅。我们不需要真正“擦除”数据，而是将其“回收”到备用链表中，以便下次复用。

1. 回收空间 (`Free_SSL`)

我们实现一个函数 Free_SSL，用于将一个被删除的元素下标 k 放回备用链表的头部

void Free_SSL(StaticLinkList space, int k) {
    space[k].cur = space[0].cur; // 将被删除元素的cur指向当前备用链表的头
    space[0].cur = k; // 将备用链表的头指针指向被删除的元素
}

2. 删除元素 (`ListDelete`)

删除第 i 个元素的代码如下：

Status ListDelete(StaticLinkList L, int i) {
    int j, k;
    if (i < 1 || i > ListLength(L)) {
        return ERROR;
    }

    k = MAXSIZE - 1; // k初始为最后一个元素的下标
    for (j = 1; j <= i - 1; j++) {
        k = L[k].cur; // 找到第i-1个元素
    }

    j = L[k].cur; // j为要删除的第i个元素的下标
    L[k].cur = L[j].cur; // 将第i-1个元素的cur指向第i+1个元素

    Free_SSL(L, j); // 将被删除的元素j回收到备用链表

    return OK;
}

执行过程详解：

通过循环找到第 i-1 个元素（“甲”）的位置，其下标为 k=1。
获取要删除元素（“乙”）的下标 j = L[1].cur = 2。
修改游标：L[1].cur = L[2].cur （即 L[1].cur = 3），让“甲”直接指向“丁”，从而跳过了“乙”。
调用 Free_SSL(L, 2)，将下标2放回备用链表的头部。

这样，“乙”就被逻辑上删除了，其占用的空间也回到了备用链表中，等待下一次被分配。

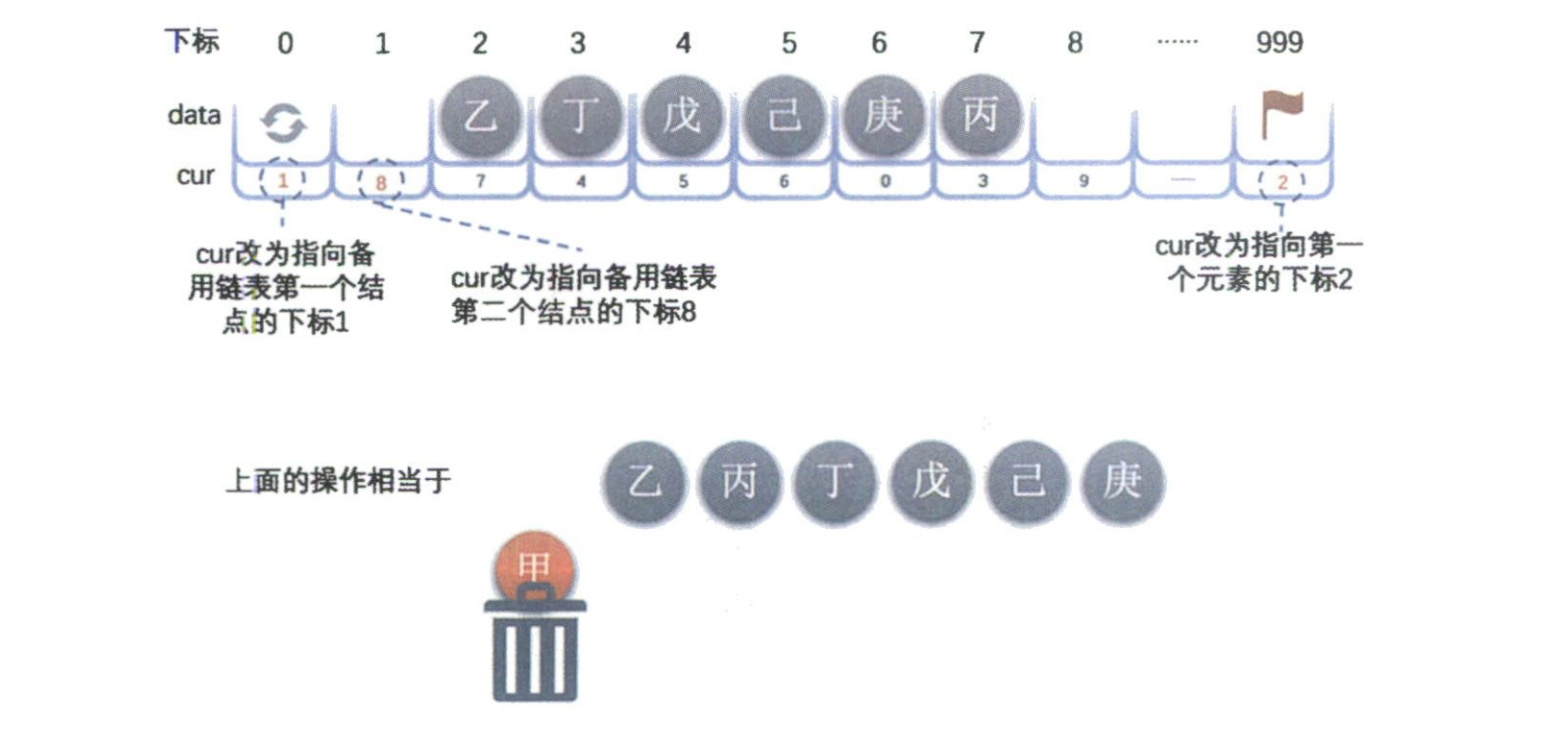
五、其他基本操作与核心优缺点

除了插入和删除，静态链表也需要实现其他基本操作，如计算长度等。

计算链表长度 (`ListLength`)

计算静态链表的长度非常直观，只需从头结点开始，沿着游标遍历，直到遇到 cur=0 的结束标志

int ListLength(StaticLinkList L) {
    int j = 0;
    int i = L[MAXSIZE - 1].cur; // 从头结点开始
    while (i) {
        i = L[i].cur; // 移动到下一个结点
        j++; // 计数器加1
    }
    return j;
}

其他如查找、遍历等操作，与线性表的基本操作类似，实现起来并不复杂。

静态链表的优缺点总结

静态链表的设计精妙，但也存在明显的优缺点：

优点：

在插入和删除操作时，只需要修改游标，不需要移动元素。这极大地改进了顺序存储结构中插入和删除需要移动大量元素的缺点，使得动态操作高效便捷。

缺点：

没有解决连续存储分配带来的表长难以确定的问题。我们必须在定义时就指定一个最大容量MAXSIZE，如果数据量超过预设值，程序就会溢出。

失去了链式存储结构随机存取的特性。由于数据在数组中是分散存储的，我们无法像访问数组那样通过下标直接定位到第i个元素，必须从头结点开始依次遍历，时间复杂度为 O(n)。

总的来说，静态链表是为了给没有指针的高级语言设计的一种实现单链表能力的方法。尽管在现代编程中可能不常用，但其背后“在约束中创造自由”的思考方式是非常巧妙的，值得我们深入理解，以备不时之需。

六、从静态链表到循环链表：解决“单行道”的烦恼

静态链表解决了无指针环境下的链表问题，但传统的单链表本身还有一个痛点：只能单向前进，无法回头。

想象一下，你是一位业务员，行程是上海 -> 苏州 -> 无锡 -> ... -> 北京。当你从北京办完事，想回上海时，你必须重新从上海出发走一遍。或者，当你在南京开会时，有人告诉你“从上海开始”，你会觉得匪夷所思——这显然是个“神经病”建议。

这个问题的本质在于，单链表的每个结点只存储了指向后继结点的指针，到达尾结点后便无路可走，无法找到前驱结点。

解决方案：循环链表 (Circular Linked List)

顾名思义，循环链表就是一个“环形”的结构。简单来说，它和静态链表最大的不同就是——最后一个元素的指针并不指向0，而是指向了链表的第一个元素，从而形成了一个闭环。数据在链表里会像轮子一样不断“循环”。

循环链表的思路非常简单：将单链表的终端结点的指针端由空指针改为指向头结点

单循环链表：终端结点指向头结点。
带头结点的循环链表：为了使空链表和非空链表的处理一致，通常也会设置一个头结点。

循环链表的结构：

typedef struct Node {
    int data;
    struct Node *next;
} Node;

在这个结构里，next指针指向链表中的下一个元素，而最后一个元素的next指针则指向头节点，形成一个循环。

循环链表的主要优势在于，无论从哪个结点出发，都可以访问到链表中的全部结点，彻底解决了“单行道”的问题。

创建一个循环链表：

Node* CreateCircularList() {
    Node *head = (Node*)malloc(sizeof(Node));  // 创建头节点
    Node *tail = head;  // 初始时头尾指向同一个节点
    for (int i = 0; i < 5; i++) {
        Node *newNode = (Node*)malloc(sizeof(Node));
        newNode->data = i;
        tail->next = newNode;  // 将新节点链接到链表末尾
        tail = newNode;  // 更新尾指针
    }
    tail->next = head;  // 最后一个元素的next指向头节点，形成闭环
    return head;
}

常见错误：

忘记闭环：如果忘记tail->next = head;，链表将变成一个普通的线性链表，而不是循环链表。
循环链表中的访问问题：循环链表不应该是“有头无尾”的，因此操作时需要确保链表在访问时能够正常地回到头部。

循环链表的优化：引入尾指针

虽然循环链表解决了遍历问题，但在某些操作上仍有不足。例如，要合并两个循环链表，如果只有头指针，我们需要遍历整个链表才能找到各自的尾结点。

为此，我们可以对循环链表进行改造：不用头指针，而是用指向终端结点的尾指针 rear 来表示循环链表。

查找终端结点：时间复杂度 O(1)，即 rear 本身。
查找开始结点：时间复杂度 O(1)，即 rear->next->next。

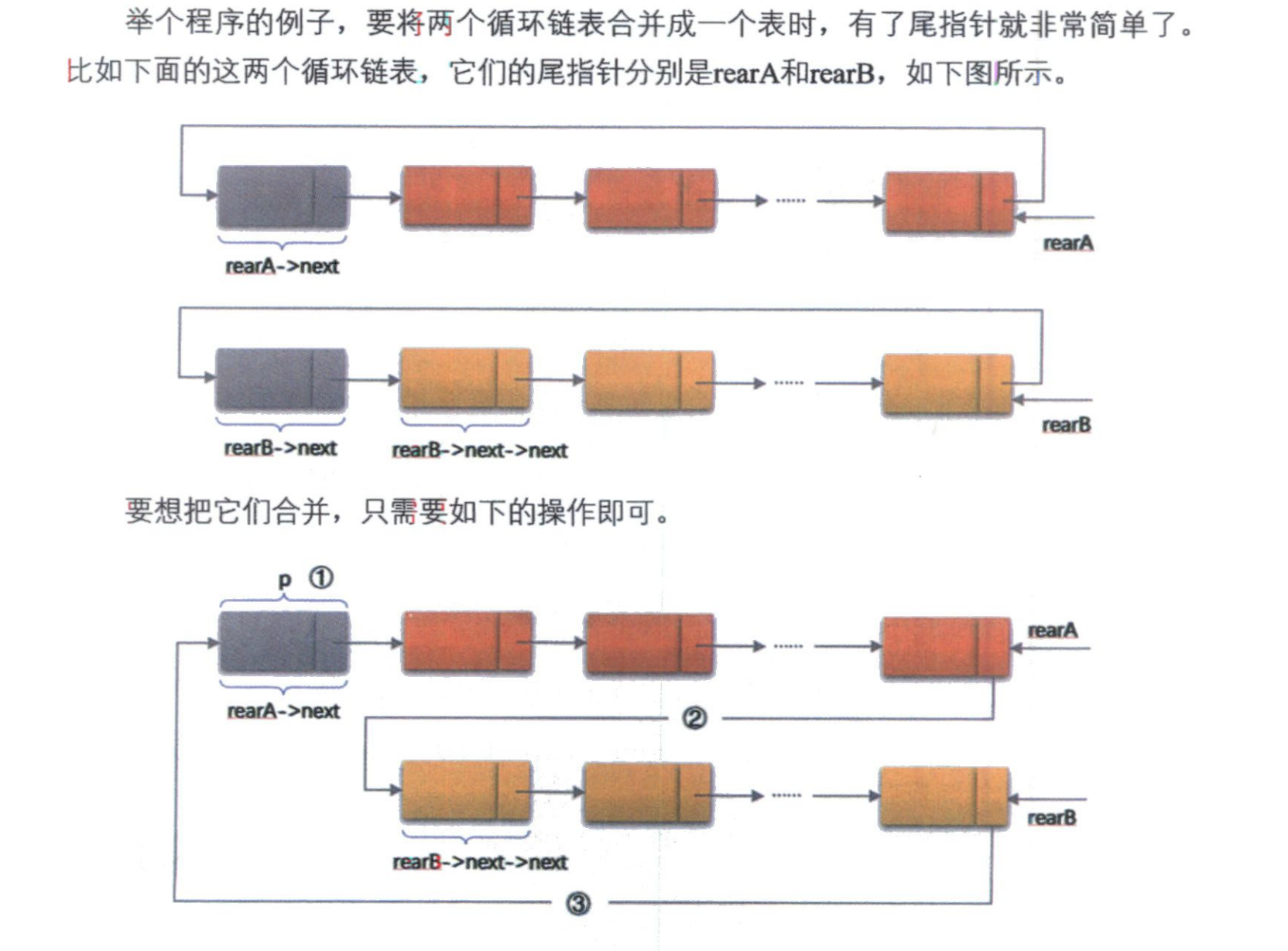
将 rearA->next 指向 rearB->next->next。
将 rearB->next 指向 rearA->next。
更新 rearA 为 rearB。

整个过程仅需常数时间，极大地提升了操作效率。

小练习：调试代码

我们来做个小练习，看看下面这段代码有没有问题：

Node* CreateCircularList() {
    Node *head = (Node*)malloc(sizeof(Node));
    Node *tail = head;
    for (int i = 0; i < 5; i++) {
        Node *newNode = (Node*)malloc(sizeof(Node));
        newNode->data = i;
        tail->next = newNode;
        tail = newNode;
    }
    // 忘了处理循环链表的闭环
    return head;
}