上取整和下取整

在数学和计算机科学中，取整函数是一类将实数映射到相近的整数的函数。^[1]

常用的取整函数有两个，分别是下取整函数和上取整函数。

下取整函数在数学中一般记作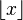或者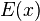，在计算机科学中一般记作floor(x)，表示不超过x的整数中最大的一个。

举例来说，，，，。对于非负的实数，其下取整函数的值一般叫做它的整数部分或取整部分。而叫做x的小数部分。每个分数都可以表示成其整数部分与一个真分数的和，而实数的整数部分和小数部分是与此概念相应的拓延。

下取整函数的符号也会用方括号表示，如[2.3]=2，称作高斯符号。而（x）则被用来表示一个数的小数部分，如（2.3）=0.3。

上取整函数在数学中一般记作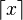，在计算机科学中一般记作ceil(x)，表示不小于x的整数中最小的一个。

举例来说，，，，。

计算机中的上取整函数和下取整函数的命名来自于英文的ceiling（天花板）和floor（地板），相关的记法由肯尼斯·艾佛森于1962年引入。^[2]

【转自wikipedia】