对数计算解析_电容值对数怎么来的-CSDN博客

本文链接：https://blog.csdn.net/doris_chuyi/article/details/146014761

对数作为数学中的一种重要工具，广泛应用于科学、工程和计算领域。它不仅简化了复杂的乘法运算，还在信号处理、数据压缩、放大器设计等实际场景中发挥着重要作用。本文将从对数的基本概念入手，探讨其计算方法及性质。

在了解对数前我们先来了解下压缩数标

压缩数标

在进行电子学测量时，如果用到比1x10-12还小，比1x1012还大的数，这说明在最小和最大数之间差值超过了1兆倍。您能画出一条数轴表示这些值吗?图1显示了这个数轴的一部分。当然，要想画出一条线能表示每个整数(可计数字)确实是不可能的。

我们用单位微法(百万分之一法拉)和皮法(万亿分之一法拉)度量电容量。用毫亨(千分之一亨)或微享(百万分之一亨)度量电感量。

当我们提到电阻值时，您会看到千欧(一千欧姆)和兆欧一百万欧姆)这样的术语。我们用兆赫兹(一百万赫兹)和千兆赫兹(十亿赫兹)度量频率。

您还能认出这些公制的前缀吗?兆(M)、毫(m)、微(μ)、皮(p)

现在让我们尝试用另一种方式来画数轴，图3只显示10倍数的数轴，这样看上去就不混乱，而且我们可以在一条数轴上显示很大范围的数。但我们仍未能显示所有的整数，那但并不是关键，只要我们可以在这些列出的数字中估计数值。不管怎样，当我们在谈论以兆计的数字时，几千就显得不是那么大了。

我们可以用 10 的幂代替所有整数来画数轴。在 10 的幂间作标记帮助估计 10 的倍数间的值

一个测定值经常在另一个值改变了很小量时而在较大范围内变化。

从低通滤波器输出的信号强度就是一个很好的例子。

业余无线发信机或接收机在它的输出端也许有个低通滤波器。这样的滤波器允许想要的信号通过。滤波器阻止高频信号，防止它们被发射出去。许多业余无线电发信机和收信机都包含内置的低通滤波器。作为预防措施，特别是老式的发信机，很多爱好者会使用一个外部滤波器。

一个滤波器效果的测试，就是给滤波器输入信号，接着测量出输出的信号。然后我们改变输入信号的频率，但保持相同的输入功率。我们测量输出强度，将其值在图中用点描出。这就是图4所表示的。

图4是滤波器输出信号强度的图像。横轴或称x轴，覆盖一个很小范围的频率。我们用普通的数标标注这根轴。纵轴或称y轴，覆盖了很大范围的输出强度，我们使用了压缩过的数标，就像图3中的数轴那样标注这个数轴。

频率标度从28兆赫(MHz)开始。低于这个频率，输入100W的功率，输出功率还是100W，滤波器对低于 30MHz的信号不起作用。在31.7MHz对，滤波器开始减少输出信号的强度。只有在高于34MHz时，滤波器将100W输入信号减少到50W输出。

在 40MHz时，对于100W的输入信号只得到不到1W 的输出信号。而当频率到达49MHz时，滤波器将 100W的输入信号减弱为大约0.0017W!

您能想象试图用线性数标来表示纵轴，画出图4吗?

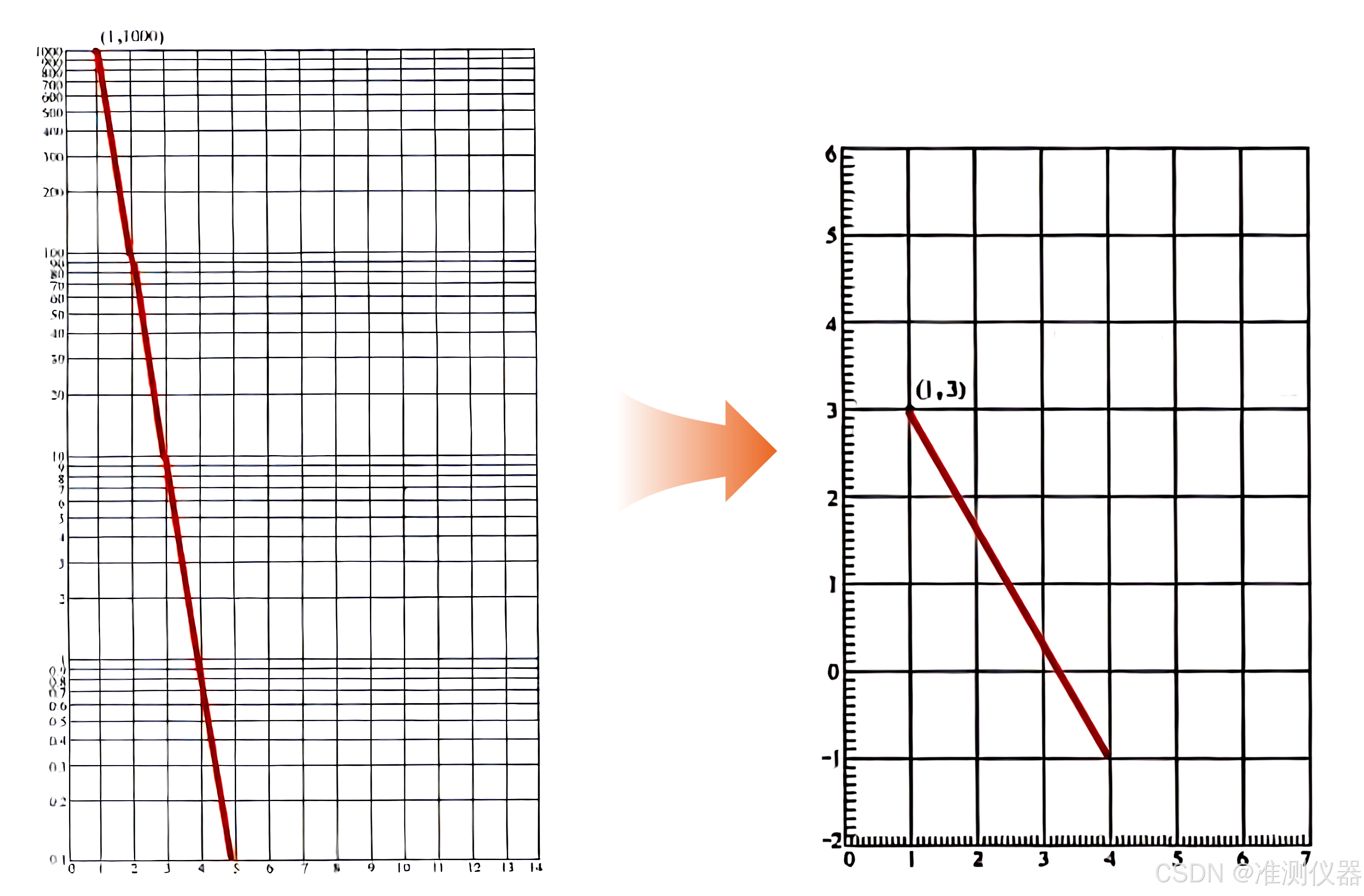
普通线性坐标系难以直观展示这些数据，而对数（Logarithm）能将指数级变化“压缩”为线性关系，让分析更高效。（图所示：压缩数标转变至对数数标）

对数是数学中的一种运算，用于简化复杂的乘法和除法运算。在电子学中，对数常用于处理电路中的信号强度、频率等参数。对数的定义如下：

对数的基本公式如下

2、常用对数和自然对数

常用对数（Common Log）：以10为底，记作log10 或简写为 log

自然对数（Natural Log）：以数学常数 e≈2.71828 为底，记作 ln 。

换底公式是将不同底数的对数转换为同一底数的对数，公式为：

这一公式在实际计算中非常有用，例如将自然对数转换为常用对数。

我们往期介绍了对数在电子学中的应用，例如在放大器设计中的增益用分贝来表示

这种表示方式简化了大数值的处理

在信号处理中对数变换在信号压缩和频谱分析中具有重要作用，例如，在图像处理中，对数变换可以增强图像的对比度

对数在电子学中有着广泛的应用，从信号强度的比较到频率的表示，再到电路中的功率计算，对数都发挥着重要作用。掌握对数的基本原理和计算方法，不仅能帮助我们更好地理解电子学中的各种现象，还能提高我们的计算效率。希望本文能帮助您在电子学的学习和工作中更加得心应手。