【论文翻译】ICDE2024 | MUSE-Net: Disentangling Multi-Periodicity for Traffic Flow Forecasting

题目	MUSE-Net: Disentangling Multi-Periodicity for Traffic Flow Forecasting MUSE-Net: 交通流量预测的多周期性解耦
论文链接	https://ieeexplore.ieee.org/abstract/document/10598118
源码	https://github.com/JianyangQin/MUSE-Net
关键词	交通流量预测，时间序列，多变量，解纠缠

摘要

精确预测交通流量在新时期构建智慧城市中发挥着关键作用。以往的研究已经成功地学习了交通流量中固有的空间和时间模式。然而，现有的工作通过纠缠学习方法研究了多周期性（例如，小时、日、周）的交通流量，这些方法尚未处理交通流量中的分布偏移和交互偏移问题。在本文中，我们提出了一种名为MUSE-Net的新型解纠缠学习网络，旨在通过同时分解交通流量中多周期模式的独特性和交互性，来克服纠缠学习的局限性。基于互信息理论，我们首先学习并解开多周期模式中的交通流量的独特和交互表示。然后，我们利用语义推动和语义拉动正则化来鼓励所学的表示独立且具有信息性。此外，我们提出了一种下界估计器，以可操作地优化具有多个变量的解纠缠问题，并提出了一种用于交通预测的联合训练模型。对多个真实世界交通数据集的实验结果证明了所提框架的有效性。

I. 引言

随着城市的快速发展，城市人口不断增加，导致人们在日常通勤中遇到的交通拥堵问题越来越多。为了应对交通拥堵，许多国家致力于大力发展智能交通系统（ITS）。此外，ITS 对于许多现实世界的应用非常重要，如公共安全和灾害控制。交通流预测在 ITS 中起到了关键作用。准确的交通流预测可以帮助交通部门设计更好的运输调度和移动管理策略。一般而言，交通流预测的目标是根据历史交通数据预测各个区域的交通流量（例如，流入和流出）。

一些早期研究提出了通过简单考虑时间和空间数据来解决交通流量预测问题。这些方法要么仅通过统计模型、循环神经网络（RNN）和 Transformer 捕获时间相关性，要么结合空间学习与时间学习，通过引入卷积神经网络（CNN）和图神经网络（GNN）来学习基于网格的或非结构化的空间依赖性。最近，一些方法提出捕获细粒度的时间信息，通过建模不同时间分辨率下（例如，每小时、每日和每周）的多个周期性来丰富时间表示。具体而言，交通序列可以被分解为接近性、周期性和趋势子序列，分别对应于每小时、每日和每周的分辨率。

然而，现有工作是以纠缠的方式学习这种多周期性的。一种纠缠学习将多周期子序列联合编码为统一表示，忽略了多周期性之间的差异。另一种纠缠学习只是简单地将多周期子序列编码分开，而不考虑多周期性之间的相似性。因此，如何解耦多周期表示中的相似性和差异仍然面临许多挑战。在多周期性建模中，主要挑战如下：

1. 分布偏移。在现实世界中，许多外部因素（例如，天气、节假日和交通事故）会影响交通并导致交通流量发生变化。因此，时间序列的分布可能会发生偏移。图1展示了分布偏移问题的两个典型案例，即水平偏移和点偏移。如果我们从所有多周期子序列中联合学习一个纠缠表示，那么建模不同子序列中存在的分布偏移将变得具有挑战性。为了解决这个问题，我们提出将多周期性解耦为几个独立的独占表示；也就是说，我们使用不同的网络来建模不同时间分辨率下的多个子序列，并保持多周期性之间的差异，从而更好地表征交通流量预测的每个多周期子序列。
   

2. 交互偏移。交互意味着观察到的时间序列可能会影响未来交通流量的预测。特别是，未来交通流量可能与多周期子序列不同地交互，每个交互可能会随时间而变化，这被称为交互偏移。图2展示了交互偏移问题的一个例子。出现这种交互偏移的原因是多个子序列之间的语义差异。特别是，接近性子序列表征短期依赖性，而趋势子序列表征长期依赖性。因此，我们提出学习一个交互表示来捕获共享多周期性信息的交通流量的共同模式，这可以缓解未来交通流量与多周期子序列之间的交互间隙。
   

3. 优化多变量解耦。在我们的案例中，我们将交通流量序列截取为多个子序列，这些子序列可以视为多个变量。最近，提出了多种方法来解耦独立的双变量。然而，随着变量数量的增加，解耦学习变得越来越困难，以应对日益增加的未知后验分布或变量之间的更复杂关系。因此，如何通过独立性和信息性优化多变量解耦仍然是一个开放问题。

在本文中，我们提出了一种新的预测网络，即多周期性解耦网络（MUSE-Net），以缓解纠缠交通流量预测的局限性，通过显式学习解耦的多周期模式。特别是，我们将接近性、周期性和趋势子序列的交通流量解耦为具有时间特性的三个独占表示，以缓解分布偏移问题，并学习一个在所有时间子序列中共享的交互表示以解决交互偏移问题。此外，我们引入了两个正则化项，即语义推送和语义拉动项。语义推送项迫使交互表示远离任意独占表示，确保交互表示独立于每个独占表示。语义拉动项迫使交互表示被拉向原始接近性、周期性和趋势子序列，鼓励交互表示学习跨不同时间子序列共享的共同模式。之后，学习到的独占和交互表示被聚合，以进一步捕获交通流量预测的空间依赖性。最后，我们提出一个下界估计器来解决难以解耦的问题，通过优化独占和交互表示的多信息量性来缓解问题。本文的主要贡献总结如下：

• MUSE-Net 提出了一个多变量解耦网络，通过解耦独占和交互表示来准确建模多周期模式，这可以处理交通流量预测的分布偏移和交互偏移。
• 我们引入了语义推送和语义拉动正则化项，以鼓励独占和交互表示的独立性和信息性。
• 我们驱动了一个下界估计器，以直接区分和优化多变量解耦学习中的问题。
• 在三个交通数据集上的广泛实验结果表明，所提出的方法相对于最先进的交通预测方法具有优越性。

II. 相关工作

在本节中，我们简要回顾了关于交通流预测和解缠学习的相关工作。

A. 交通预测

随着城市的快速发展，交通预测模型（模拟交通状况随时间和地区变化的模型）引起了越来越多的研究关注。作为代表性方法，循环网络（如长短期记忆网络（LSTM）和门控循环单元网络（GRU））从长序列中学习时间相关性。在空间学习方面，卷积神经网络（CNN）已广泛应用于网格单元数据的交通预测中。相比于基于CNN的方法，图神经网络（GNN）的方法被推广用于挖掘非线性结构数据的空间依赖性。例如，数据驱动的时空图神经网络（STGNN-DJD）开发了两个新的图模型来模拟流动特征和模式关联。此外，一些研究引入了注意力机制，通过自适应地关注预测数据中最相关的特征，更好地学习来自交通的上下文信息。例如，时空小波（STWave）通过解缠双通道网络模拟趋势和事件，然后通过图注意力机制捕捉动态空间相关性。

尽管这些方法显著提高了交通预测的性能，但它们是解缠学习的方式，缺乏对交通预测中多周期模式的深思熟虑的考虑。例如，现有方法难以通过学习多周期性的统一表示来捕捉不同时间维度中的固有模式。虽然一些方法通过门控机制和卷积分别对多周期性进行编码和融合，但它们难以区分不同多周期性模式之间的相似性和差异，从而学习到冗余信息。相比之下，我们提出的方法显式地解耦了纠缠的时间序列为独立且交互的表示，不仅捕捉每个时间子序列的特有模式，还捕捉了多个子序列之间的共同模式。通过这种方式，我们提出的方法能够有效地克服分布漂移和交互漂移问题。

B. 解缠学习

解缠学习的目的是将观测数据分解为几个不同的表示，这些表示表征了潜在的解释性因素。变分自编码器（VAE）及其变体β-VAE是学习潜在表示的代表性解缠方法。基于VAE，一些研究提出了二元解缠。例如，跨域解缠网络（CdDN）和交互信息自动编码器（IIAE）提出了跨域解缠，以学习特定领域和跨领域的共享表示，用于图像到图像的翻译任务。与VAE不同，一些方法如信息最大化生成对抗网络（InfoGAN）和解缠图对比学习（DGCL）采用生成对抗网络（GAN）和对比学习，通过最大化变量和输入之间的互信息来学习解缠表示。对于时空预测，提出了时空归一化（ST-Norm），通过将观察数据解缠为高频分量和局部分量。

尽管二元解缠方法取得了显著成功，但它们难以推广到多变量场景。随着变量数量的增加，如何确定一个解缠表示对其他表示的影响成为一个问题。一种可行的解决方案是估计不同变量之间的互信息，但通过互信息优化多变量解缠仍然是一个具有挑战性的问题，因为变量的后验分布难以处理。为此，我们提出了一种联合训练模型，并推导出一个下界估计器来优化带有互信息评估的多变量解缠。

III. 预备知识

在本文中，我们重点关注交通流预测，并简要回顾交通流预测的定义和符号。

定义 1（空间区域）

有很多种定义可以用于建模城市中的区域。在本研究中，我们采用传统的网格定义，将城市划分为$H\times W$的网格图，基于经纬度将城市划分为相同大小的网格，每个网格代表一个空间区域$r_{h,w}$（$h\in [1,\cdots ,H]$, $w\in [1,\cdots ,W]$）。网格图考虑了区域内的交通状况，并有助于设计区域的交通调度和管理。例如，共享单车公司可以使用区域的交通流量来决定在这些区域内应放置多少辆自行车。

定义 2（流入/流出）

在基于网格的划分之后，我们将第$i$个时间间隔内的交通流量分布表示为张量$X_i\in {\mathbb{R}}^{2\times H\times W}$，其中$(X_i{)}_{0,h,w}=x_i^{0,h,w}$和$(X_i{)}_{1,h,w}=x_i^{1,h,w}$分别表示区域$(h,w)$的流出量和流入量。形式化地，流出量和流入量定义如下：公式(1-2)

x i 0 , h , w = ∑ M r k ∈ P { ∣ { i > 1 ∣ u i − 1 ∈ ( h , w ) ∩ u i ∉ ( h , w ) } ∣ } , x_i^{0,h,w} = \sum_{M_{r_k} \in \mathcal{P}} \left\{ | \{i > 1 | u_{i-1} \in (h, w) \cap u_i \notin (h, w)\}| \right\}, xi0,h,w​=Mrk​​∈P∑​{∣{i>1∣ui−1​∈(h,w)∩ui​∈/(h,w)}∣},

x i 1 , h , w = ∑ M r k ∈ P { ∣ { i > 1 ∣ u i − 1 ∉ ( h , w ) ∩ u i ∈ ( h , w ) } ∣ } , x_i^{1,h,w} = \sum_{M_{r_k} \in \mathcal{P}} \left\{ | \{i > 1 | u_{i-1} \notin (h, w) \cap u_i \in (h, w)\}| \right\}, xi1,h,w​=Mrk​​∈P∑​{∣{i>1∣ui−1​∈/(h,w)∩ui​∈(h,w)}∣},

其中$|\cdot |$表示集合的基数，$\mathcal{P}$表示第$i$个时间间隔内的轨迹集合。$M_{r_k}:u_1\to u_2\to \cdots \to u_{|M_{r_l}|}$是$\mathcal{P}$中的轨迹，且$u_k\in (h,w)$表示空间点$u_k$位于区域$(h,w)$内，反之亦然。

定义 3（接近性/周期性/趋势）

为了研究交通的多重周期性，交通流的时间序列可以被截取为具有不同分辨率的三个子序列，即接近性（$C$）、周期性（$P$）和趋势（$T$）。在本文中，我们选择小时、日和周的分辨率来表示接近性、周期性和趋势子序列，因为交通流通常变化较快。假设采样频率为$f$次/天，$C$、$P$和$T$的长度分别为$L_c$、$L_p$、$L_t$。接近性、周期性和趋势子序列在第$i$个时间间隔内可以定义如下：公式(3-5)

$$C_i=[X_{i-L_c+1},X_{i-L_c+2},\cdots ,X_i],$$

$$P_i=[X_{i-L_p\times f},X_{i-(L_p-1)\times f},\cdots ,X_{i-1\times f}],$$

$$T_i=[X_{i-L_t\times f\times 7},X_{i-(L_t-1)\times f\times 7},\cdots ,X_{i-1\times f\times 7}].$$

值得注意的是，多重周期性（即接近性、周期性和趋势）也可以根据不同的预测需求定义为其他分辨率，例如{分钟、小时、日}用于短期预测，{日、月、年}用于长期预测。

定义 4（交通流预测）

给定历史观测数据 { X i ∣ i = 0 , ⋯   , n − 1 } \{X_i | i = 0, \cdots, n-1\} {Xi​∣i=0,⋯,n−1}，一步交通流预测的目标是找到一个模型$\mathcal{F}$，该模型使用多重周期的观测子集来预测下一时间戳的区域流入和流出量，公式(6)

$$Y_n=\mathcal{F}(C_{n-1},P_{n-1},T_{n-1}),$$

多步交通流预测旨在使用多个多重周期的观测子集来预测下一$l$个时间步长的区域流入和流出量。公式(7)

$$\sum _{j=n}^{n+l-1}{Y}_j=\mathcal{F}\left(\sum _{j=n-l}^{n-1}(C_{n-j},P_{n-j},T_{n-j})\right).$$

IV. 方法

我们的 MUSE-Net 首先提出了解缠、语义推送和语义拉动模块来建模时间多重周期性。然后，采用现有的 ResPlus 网络来捕捉空间依赖性。在此之后，我们引入了一种优化和联合训练程序来解决交通流预测的解缠问题。

A. 解缠

为了解决解缠学习的局限性，我们旨在将接近性、周期性和趋势子序列的流量解缠为相应的独立表示和交互表示。每个独立表示都旨在捕获相应时间子序列的私有特性，这对于建模时间序列的水平变化和点变化非常有用。此外，交互表示与交通流的常见模式的目标是减少多个时间序列之间的语义差距，这对于缓解交互漂移问题至关重要。也就是说，独立表示可以描述高峰期间的交通动态，而交互表示可以描述非高峰期间的交通稳定性。

我们假设某些随机过程生成了一组三元时间子序列，即$(c,p,t)\sim q_D(c,p,t)$，其中三元组的每个元素$c\in C$、$p\in P$和$t\in T$分别从接近性、周期性和趋势子序列中提取，$q_D(\cdot )$是一个未知的真实联合分布。这个时间三元组可以分解为四个部分，包括独立表示$z^c\in Z^C$、$z^p\in Z^P$和$z^t\in Z^T$，以及交互表示$z^s\in Z^S$，这可以重写为一个边际似然最大化问题：公式(8)

$$\max {\mathcal{L}}_{dis}=\max q_{\theta }(c,p,t)$$

$$=\max \int d{z}^{c}d{z}^{p}d{z}^{t}d{z}^s{q}_{{\theta }_c}(c|z^c,z^s)q_{{\theta }_p}(p|z^p,z^s)$$

$$q_{{\theta }_t}(t|z^t,z^s)q(z^c)q(z^p)q(z^t)q(z^s),$$

其中$q_{\theta }(c,p,t)$是一个生成分布，用于逼近未知的真实分布$q_D(c,p,t)$，$\theta$是模型的参数。

B. 语义推送

尽管我们将多个时间子序列解缠为独立和交互表示，但不能确保没有流模式在任何解缠表示之间共享。为了解决这个问题，我们提出将交互表示从任意独立表示中推开，使得每个表示在语义上都是独立的。为此，我们最小化每个独立表示和交互表示之间的互信息，这相当于一个最大化问题，公式(9)如下：

$$\max {\mathcal{L}}_{push}=\max ({\mathcal{L}}_{push}^c+{\mathcal{L}}_{push}^p+{\mathcal{L}}_{push}^t),$$

其中

$${\mathcal{L}}_{push}^c=-I(Z^C;Z^S),{\mathcal{L}}_{push}^p=-I(Z^P;Z^S),\text{和}{\mathcal{L}}_{push}^t=-I(Z^T;Z^S)$$

分别表示关于接近性、周期性和趋势子序列的互信息。为了更好地理解互信息在解缠表示中的作用，我们以${\mathcal{L}}_{push}^c$为例，并在交互信息的帮助下重写$Z^C$和$Z^S$之间的互信息：公式(10)

$${\mathcal{L}}_{push}^c=-I(Z^C;Z^S)$$

$$=-I(C;Z^C)+I(Z^C;C|Z^S)-I(Z^C;Z^S|C)$$

由于$Z^S$从$C$中学习，我们有$q(z^c|c)=q(z^c|c,z^s)$。因此，上述公式的最后一项消失，即$I\left(Z^C;Z^S\mid C\right)=H\left(Z^C\mid C\right)-H\left(Z^C\mid C,Z^S\right)=0,$ 公式(11)

$${\mathcal{L}}_{push}^c=-I(C;Z^C)-I(C;Z^S)+I(C;Z^C,Z^S).$$

在公式中，前两项与最后一项对立，使得$Z^C$和$Z^S$能够捕获接近性子序列$C$的互斥信息。此外，${\mathcal{L}}_{push}^p$和${\mathcal{L}}_{push}^t$的互信息可以像${\mathcal{L}}_{push}^c$一样获得，由于篇幅限制，此处不再详细描述。

C. 语义拉动

为了使学习到的交互表示能够完全捕捉到多个时间子序列之间共享的交通流的共同模式，我们建议将交互表示拉向原始的接近性、周期性和趋势子序列。为此，我们通过最大化交互信息来量化交互表示和多个时间子序列之间的共享信息量，公式(12)如下：

$$\max {\mathcal{L}}_{pull}=\max I(C;P;T;Z^S)$$

由于公式具有对称性，我们可以将交互信息$I(C;P;T;Z^S)$重写为关于接近性、周期性和趋势子序列的以下目标：公式（13-15）

$${\mathcal{L}}_{pull}^c=I(C;Z^S)-I(C;Z^S|P)-I(C;Z^S|T)+I(C;Z^S|P,T),$$

$${\mathcal{L}}_{pull}^p=I(P;Z^S)-I(P;Z^S|C)-I(P;Z^S|T)+I(P;Z^S|C,T),$$

$${\mathcal{L}}_{pull}^t=I(T;Z^S)-I(T;Z^S|C)-I(T;Z^S|P)+I(T;Z^S|C,P).$$

可以看出，公式中包含四项。第一项鼓励$Z^S$从$C$中学习信息。第二和第三项是丢弃与$P$和$T$分别相关的$Z^S$中的一些信息。最后一项是恢复第二项和第三项反复丢弃的一些信息。为了联合考虑接近性、周期性和趋势子序列，语义拉动的目标可以重新表述为：公式（16）

$$\max {\mathcal{L}}_{pull}=\max 3\cdot I(C;P;T;Z^S)$$

$$=\max ({\mathcal{L}}_{pull}^c+{\mathcal{L}}_{pull}^p+{\mathcal{L}}_{pull}^t).$$

D. 优化

我们的目标是基于解缠的独立和交互表示来预测未来的交通流量。为此，我们训练 MUSE-Net 通过回归损失${\mathcal{L}}_{reg}$ 来预测未来的交通流量，该损失最小化预测值$Y_n$和真实值$X_n$之间的差异，同时在语义推送和拉动的正则化下进行解缠。结合公式(8)、(9)、(16) 和回归损失，我们可以推导出多变量解缠问题的整体目标，如下所示：公式（17）

$$\underset{q_{\theta },r_{\varphi }}{\max }{\mathcal{L}}_{Dis}+\lambda ({\mathcal{L}}_{Push}+{\mathcal{L}}_{Pull})-{\mathcal{L}}_{Reg},$$

其中$\lambda$是一个平衡参数，用于权衡交互表示与独立表示捕获的信息量。可以看出，所提出的目标函数与现有的基于解缠的方法显著不同。一方面，所提出的解缠考虑了多变量场景，使解缠更具可操作性。另一方面，所提出的方法采用互信息来量化解缠表示之间的信息量，鼓励解缠的区分。然而，由于互信息正则化项（即语义推送和拉动）给多变量解缠带来了几个难以处理的积分，因此直接优化公式(17)是不可行的。因此，我们理论上推导了一个下界估计器，以更直接地优化多变量解缠问题，如下所示。

优化 ${\mathcal{L}}_{dis}$

由于交互表示$z^s$和真实参数${\theta }^{\ast }$未知，优化${\mathcal{L}}_{dis}$是不可行的。受[50]的启发，公式(8) 可以重写为边际似然的下界，并通过变分推断进行优化：公式（118）

$${\mathcal{L}}_{dis}=\log q_{\theta }(c,p,t)\ge {\mathbb{E}}_{r_{\varphi }(z^c,z^p,z^t,z^s|c,p,t)}\left[\log \frac{q_{\theta }(c,p,t,z^c,z^p,z^t,z^s)}{r_{\varphi }(z^c,z^p,z^t,z^s|c,p,t)}\right],$$

其中$r_{\varphi }(z^c,z^p,z^t,z^s|c,p,t)$是一个逼近于真实后验分布$q_{\theta }(c,p,t,z^c,z^p,z^t,z^s|c,p,t)$的分布，可以计算如下：公式（19）

$$r_{\varphi }(z^c,z^p,z^t,z^s|c,p,t)=r_{\varphi }(z^c|c)r_{\varphi }(z^p|p)r_{\varphi }(z^t|t)r_{\varphi }(z^s|c,p,t).$$

因此，我们将公式(18) 重写为以下不等式(20)：

L d i s ≥ ∑ i ∈ { c , p , t } E r ϕ ( z i ∣ i ) r ϕ ( z s ∣ c , p , t ) [ log ⁡ q θ ( i ∣ z i , z s ) r ϕ ( z i ∣ i ) ] − ∑ i ∈ { c , p , t } D K L [ r ϕ ( z i ∣ i ) ∣ ∣ q θ ( z i ) ] − D K L [ r ϕ ( z s ∣ c , p , t ) ∣ ∣ q θ ( z s ) ] . \mathcal{L}_{dis} \geq \sum_{i \in \{c, p, t\}} \mathbb{E}_{r_\phi(z^i | i)} r_\phi(z^s | c, p, t) \left[ \log \frac{q_\theta(i | z^i, z^s)}{r_\phi(z^i | i)} \right] - \sum_{i \in \{c, p, t\}} D_{KL} \left[ r_\phi(z^i | i) || q_\theta(z^i) \right] - D_{KL} \left[ r_\phi(z^s | c, p, t) || q_\theta(z^s) \right]. Ldis​≥i∈{c,p,t}∑​Erϕ​(zi∣i)​rϕ​(zs∣c,p,t)[logrϕ​(zi∣i)qθ​(i∣zi,zs)​]−i∈{c,p,t}∑​DKL​[rϕ​(zi∣i)∣∣qθ​(zi)]−DKL​[rϕ​(zs∣c,p,t)∣∣qθ​(zs)].

优化 ${\mathcal{L}}_{push}$

优化 $ \mathcal{L}{\text{push}} $。 $ \mathcal{L}{\text{push}} $是难以处理的，因为 $ q_D© $、$ q_D§ $ 和 $ q_D(t) $ 的分布未知；因此，我们应用变分信息瓶颈（VIB）来简化和优化公式（9）。以关于邻近度的语义推动目标（即公式（11））为例，第一项 $ -I(C; Z^C) $ 和第二项 $ -I(C; Z^S) $ 可以分别通过使用 $ -\mathbb{E}{q_D©} [D{KL} [r_\phi(z^C|c) \parallel q_\theta(z^C)]] $ 和 $ -\mathbb{E}{q_D©} [D{KL} [r_\phi(z^S|c) \parallel q_\theta(z^S)]] $ 作为它们的下界进行近似，其中 $ q_\theta(z^C) $ 和 $ q_\theta(z^S) $ 可以定义为标准高斯分布。此外，我们可以通过使用生成分布 $ q_\theta(c|z^C, z^S) $ 最大化最后一项 $ I(C; Z^C, Z^S) $ 的下界，公式(21)如下：

$$I(C;Z^C,Z^S)={\mathbb{E}}_{r_{\varphi }(z^C,z^S|c)q_D(c)}\left[\log \frac{r_{\varphi }(c|z^C,z^S)}{q_D(c)}\right]=H(C)+{\mathbb{E}}_{r_{\varphi }(z^C,z^S|c)q_D(c)}\left[q_{\theta }(c|z^C,z^S)\right]+{\mathbb{E}}_{r_{\varphi }(z^C,z^S)}\left[D_{KL}\left[r_{\varphi }(c|z^C,z^S)\parallel q_{\theta }(c|z^C,z^S)\right]\right]\ge H(C)+{\mathbb{E}}_{r_{\varphi }(z^C,z^S|c)q_D(c)}\left[q_{\theta }(c|z^C,z^S)\right].$$

因此，关于邻近度子序列的语义推动目标可以被推导如下：公式(22)

$${\mathcal{L}}_{\text{push}}^C\ge -{\mathbb{E}}_{q_D(c)}\left[D_{KL}\left[r_{\varphi }(z^C|c)\parallel q_{\theta }(z^C)\right]\right]-{\mathbb{E}}_{q_D(c)}\left[D_{KL}\left[r_{\varphi }(z^S|c)\parallel q_{\theta }(z^S)\right]\right]+{\mathbb{E}}_{r_{\varphi }(z^C,z^S|c)q_D(c)}\left[q_{\theta }(c|z^C,z^S)\right].$$

优化 ${\mathcal{L}}_{pull}$

与优化 $L_{\text{push}}$ 类似，我们应用 VIB 技术来优化难以处理的 $L_{\text{pull}}$（即，方程 (16)）。以语义拉近目标为例（即方程 (13)），最后一项 $I\left(C;Z^S\mid P,T\right)$ 的下界可以通过对配对子序列 $P$ 和 $T$ 引入变分分布 $d_{\omega }^{p,t}\left(z^s\mid p,t\right)$ 来最大化，具体如下：公式(23)

对于第二项 $I\left(C;Z^S\mid P\right)$ 和第三项 $I\left(C;Z^S\mid T\right)$，我们可以通过引入变分分布 $d_{\omega }^{c,p}\left(z^s\mid p\right)$ 和 $g_{\tau }^p\left(z^s\mid p\right)$，导出第二项的下界，类似地得到第三项：公式(24)

因此，我们可以导出关于子序列接近性的语义拉近目标，具体如下：

整体目标函数

在获得${\mathcal{L}}_{dis}$、${\mathcal{L}}_{push}$ 和${\mathcal{L}}_{pull}$ 的下界后，我们可以通过合并和消除项将整体目标函数（即公式(17)）重新表述为：公式(26)

$$\underset{q_{\theta },r_{\varphi }}{\max }{\hat{\mathcal{L}}}_{Dis}+{\hat{\mathcal{L}}}_{Push}+{\hat{\mathcal{L}}}_{Pull}-{\mathcal{L}}_{Reg},$$

其中

E. 联合训练

公式(26) 的整体目标函数由四个组成部分组成。具体而言，公式(27)、(28)、(29) 和(30) 分别表示解缠、语义推送、语义拉动和预测单元。为了实现这一目标，我们提出了一个联合训练框架，如图3所示。

联合训练框架的细节如下：

在公式(27)中，我们提出了一个独立编码器来学习独立信息。独立编码器首先以时间子序列作为输入（例如，$C$），然后利用卷积层来编码时间子序列的独立表示（例如，$Z^C$）并利用全连接层提取表示的分布（例如，$r_{\varphi }(z^c|c)$）。与此同时，我们提出了一个交互编码器来学习交互信息。交互编码器将三元时间子序列（包括$C$、$P$ 和$T$）的卷积特征作为输入，并由两部分组成：一个用于学习交互表示（例如，$Z^S$）的卷积层和一个用于学习相应分布（例如，$r_{\varphi }(z^s|c,p,t)$）的全连接层。

在公式(28)中，我们将生成分布$q_{\theta }(c|z^c,z^s)$作为重构解码器。重构解码器旨在通过使用全连接层基于相应的独立（例如，$Z^C$）和交互表示（例如，$Z^S$）重建时间子序列（例如，$\hat{C}$）。

在公式(29)中，我们提出了一个单重变分编码器来逼近单个时间子序列（例如，$g_{\tau }^{c,p}(z^s|p)$）的变分分布和一个双重变分编码器来逼近成对时间子序列（例如，$d_{\omega }^{p,t}(z^s|p,t)$）的变分分布。单重变分编码器以时间子序列（例如，$P$）的卷积特征作为输入，并通过卷积层和全连接层的组合提取变分分布。双重变分编码器类似于单重变分编码器，但它以成对的时间子序列（例如，$P$ 和$T$）作为输入。

在公式(30)中，我们的目标是将预测$Y_n$拟合到基于学习到的独立和交互表示的真实未来交通流$X_n$。因此，我们采用了ResPlus网络，它旨在建模空间依赖性，融合独立和交互表示，并生成未来交通流$Y_n$的预测。

根据DeepSTN+，我们设置接近性、周期性和趋势子序列的长度（即$L_c$、$L_p$ 和$L_t$）为3、4 和4步长。学习到的独立和交互表示的维度设置为$d=64$。表示的分布由均值和标准差表示。经验上，我们采样独立表示的维度$k/4$的均值和标准差，同时采样交互表示的维度$k=128$的均值和标准差。

F. 复杂度分析

表I列出了提出的MUSE-Net与代表性的基于CNN、GCN和注意力机制的基线模型（包括DeepSTN+、DMSTGCN和GMAN）在时间和空间复杂度上的比较，其中$L=L_c+L_p+L_t$，$d$，$M=H\times W$和$E$分别表示多周期序列的长度、表示维度、网格大小和图中的边数。由于提出的MUSE-Net主要依赖于卷积，因此MUSE-Net的时间复杂度为$\mathcal{O}(LdM+d^{2}M)$。如表I所示，由于$L,d\ll M$，MUSE-Net的速度可以快于GMAN。此外，如果图是稠密的，即$E\to M^2$，则DMSTGCN的时间复杂度将高于所提出的方法。在空间复杂度方面，虽然所提出的MUSE-Net需要比DMSTGCN和GMAN稍多的内存，但MUSE-Net的空间复杂度与基线方法相同，因为这些方法的空间复杂度均为$M^2$。考虑到MUSE-Net在实验中取得的优异性能（请参见实验部分的表II），所提出方法的空间复杂度是可以接受的。

V. 实验

在本节中，我们在三个公共基准数据集上评估我们提出的MUSE-Net，并与最先进的交通流预测方法进行比较，总结出以下研究问题：

• RQ1: 我们提出的MUSE-Net在交通流预测中能否优于基线模型？
• RQ2: 不同组件的设计是否对模型的性能有贡献？
• RQ3: 解缠的独立和交互表示是否彼此独立？
• RQ4: 独立和交互表示是否能够提供足够的信息进行预测？
• RQ5: 独立和交互表示是否能够解释特定的交通流模式？
• RQ6: MUSE-Net的超参数如何影响预测任务的性能？

A. 数据集

我们在三个真实世界的基准数据集上评估所提出的方法，具体如下：

• NYC-Bike: NYC-Bike数据集包括2016年7月1日至2016年8月29日期间纽约的自行车轨迹。按照[53]的做法，我们首先将整个城市划分为10×20的网格图。每个网格的大小约为1km × 1km。然后，我们选择前40天的数据（即2016年7月1日至2016年8月9日）作为训练集，最后20天的数据作为测试集。

• NYC-Taxi: NYC-Taxi数据集包括2015年1月1日至2015年3月1日期间纽约的出租车轨迹。按照[53]的做法，我们首先将整个城市划分为10×20的网格图。每个网格的大小约为1km × 1km。然后，我们选择前40天的数据（即2015年1月1日至2015年2月10日）作为训练集，最后20天的数据作为测试集。

• TaxiBJ: TaxiBJ数据集包括2013年1月1日至2013年10月30日期间采集的出租车GPS轨迹。按照[16]的做法，我们首先将整个城市划分为32×32的网格图。每个网格的大小约为0.6km × 0.6km。然后，我们选择最后20天的数据（即2013年10月11日至2013年10月30日）作为测试集，剩余的数据作为训练集。

在我们的实验中，每个时间间隔的长度设置为30分钟。我们使用tanh作为最后的激活函数，其输出范围在-1到1之间。因此，我们通过训练中的Min-Max归一化将数据缩放到[-1, 1]范围内，并在评估过程中将预测值重新缩放回正常值以与真实值进行比较。此外，我们选择90%的训练数据来拟合模型，剩下的10%用于验证。

B. 基线与实现

我们使用Keras框架实现了提出的模型，并使用Adam优化器进行训练，学习率为0.0002，批量大小为8，最大迭代次数为350。对于目标函数，平衡系数$\lambda$设置为1，以权衡信息学习。然后，我们将MUSE-Net与以下11个基线进行比较，这些基线可以分为五类：基于RNN的模型（RNN、Seq2Seq）、基于CNN的模型（CONVGCN、DeepSTN+）、基于GNN的模型（ASTGCN、DMSTGCN、STGNN、ST-SSL）、基于注意力机制的模型（GMAN、STGSP）和基于解缠的模型（ST-Norm）。

• RNN: 它利用循环神经网络捕捉时间序列数据的时间效应，以进行交通流量预测。
• Seq2Seq: 这是一个编码器-解码器框架，使用门控循环神经网络来预测交通流。
• ASTGCN: 包含一个时空组件，其中图卷积网络和卷积网络分别学习空间和时间信息，并且有一个注意力组件来捕捉时空相关性。
• CONVGCN: 结合了图卷积和3D卷积，以捕捉交通流预测的短期和长期空间依赖性。
• GMAN: 设计了一个编码器-解码器框架，使用转换注意机制将历史交通流转换为未来交通流。
• STGNN: 结合位置感知图神经网络与基于循环的Transformer层，共同捕捉空间和时间依赖性以进行交通流预测。
• DMSTGCN: 通过具有膨胀卷积层的动态图卷积网络探索交通流的时间特定空间依赖性。
• ST-Norm: 提出了一种时间和空间归一化方法，分别对高频和局部组件进行细化以建模交通流模式。
• STGSP: 基于Transformer的方法，可以通过多头注意机制建模多周期模式的动态相关性。
• DeepSTN+: 通过卷积神经网络联合学习时间和空间依赖性，以预测未来的交通流。
• ST-SSL: 提出了一个自监督学习范式，以模型交通流预测中的空间和时间异质性。

对于ASTGCN、CONVGCN、GMAN、DMSTGCN和ST-Norm方法，我们仔细修改了预测层的输出通道数，从1改为2，以联合预测流入和流出。对于STGSP方法，我们不利用外部信息（例如日期和天气）来预测交通流，以确保公平比较。对于其余的基线，我们采用其原始网络并按照论文中报告的最佳参数进行实验。

所有实验都在Linux服务器上进行（CPU: Intel® Xeon® Gold 6138 CPU @ 2.00GHz，GPU: NVIDIA Tesla V100 GPU 32GB）。此外，我们采用平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）作为衡量不同方法预测性能的指标。对于MAE、RMSE和MAPE指标，数值越小表示预测性能越好。

C. 性能比较 (RQ 1)

为了全面评估我们提出的MUSE-Net的性能，我们首先在一步预测和多步预测设置中进行了对比实验。然后，我们进一步评估了MUSE-Net在高峰与非高峰和工作日与周末期间的预测表现，以了解在不同交通条件下的预测差异。最后，我们可视化了MUSE-Net的预测结果。

一步预测是交通流预测中的基本任务。在我们的实验设置中，我们基于历史多周期数据预测下一个时间步的时间序列的交通流量。表II列出了MUSE-Net与NYC-Bike、NYC-Taxi和TaxiBJ数据集中的11个基线的性能比较。表中MUSE-Net所取得的改进百分比定义为$\frac{\text{Best baseline result}-\text{Ours result}}{\text{Best Baseline result}}\times 100\%.$

我们可以观察到，基于RNN的模型（如RNN和Seq2Seq）由于忽略了交通流的空间依赖性，因此表现不佳。对于基于CNN和GNN的模型，MUSE-Net可以通过减少RMSE误差在三个数据集中分别优于DeepSTN+和ST-SSL。这是因为CNN和GNN模型忽视了时间顺序依赖性，而提出的方法能够通过交互表示捕捉短期和长期时间序列之间的相关性。在基于注意力机制的模型中，GMAN和STGSP能够自适应地提取交通流模式；然而，MUSE-Net表现更好。与STGSP相比，MUSE-Net在三个数据集中在RMSE上可产生20%至35%的改进。可能的原因是注意力机制模型学习了交通流的缠绕表示，而MUSE-Net联合学习了解缠的独立和交互表示，以更好地表征交通流模式。此外，所提出的方法在与基于解缠模型（即ST-Norm）的比较中，在RMSE上至少获得了11%的改进，这验证了MUSE-Net在建模多周期性方面的合理性。

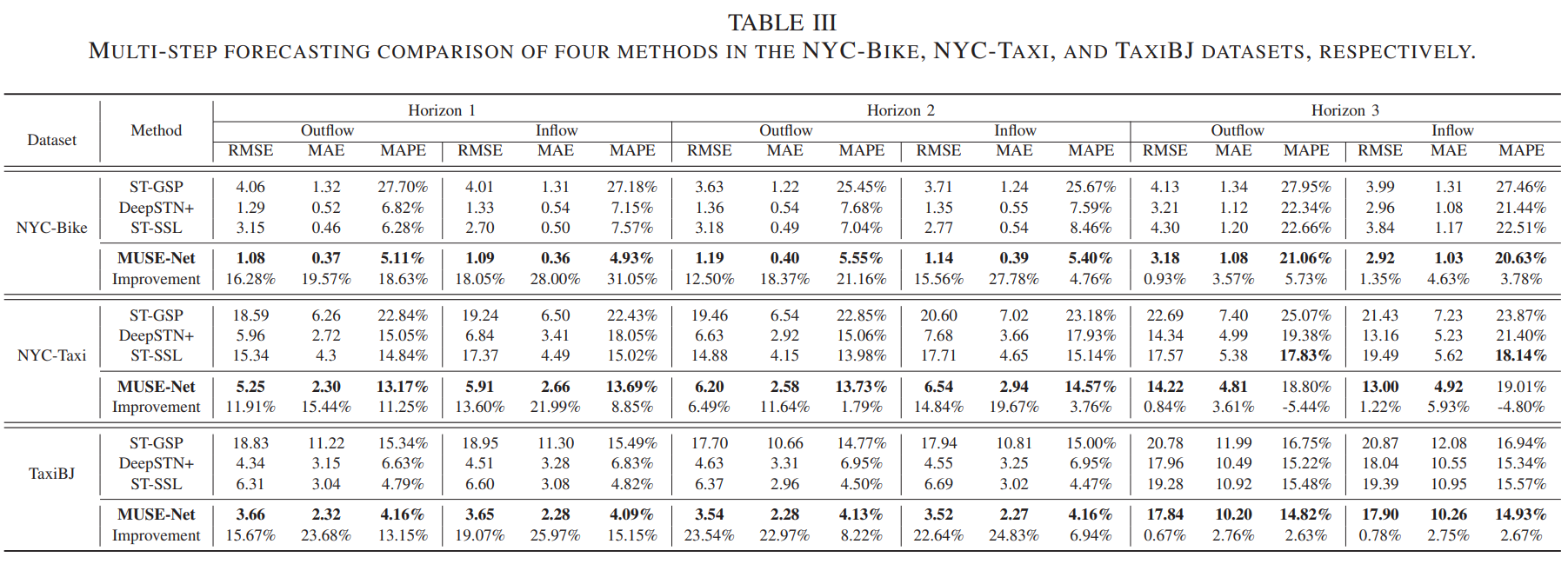
与一步预测相比，多步预测不仅要考虑下一个时间步的交通流，还要考虑后续的多个时间步。在我们的实验设置中，多步预测是为了预测三个时间步后的交通流（即1.5小时后），每个时间步的交通流特征由对应的历史多周期交通流（包括接近性、周期性和趋势数据）来描述。由于多个多周期交通流不连续且可能存在语义差距，我们选择了三种基于多周期的方法作为基线进行比较。表III列出了三个方法的多步预测结果。可以看出，我们的MUSE-Net在三个数据集中取得了显著的增益。与顺序处理多周期流的ST-GSP相比，DeepSTN+、ST-SSL和MUSE-Net分别分离了接近性、周期性和趋势流，并分别处理每个周期流，从而能够充分利用每个多周期子序列的特定信息，以获得更好的性能。此外，DeepSTN+、ST-SSL和MUSE-Net利用了多周期数据的全局信息，使得前两个时间步的预测可能比最后一个时间步的预测更准确。与DeepSTN+和ST-SSL相比，MUSE-Net进一步捕捉到了独立和交互的交通模式，导致了更好的多步预测性能。

由于人们的出行需求在高峰与非高峰以及工作日与周末期间不同，我们进一步进行了实验，以评估MUSE-Net在高峰与非高峰以及工作日与周末期间的预测表现。对于高峰与非高峰实验，我们选择了上午7:00至9:00和下午5:00至7:00的时间段作为高峰期，其余时间段作为非高峰期。对于工作日与周末实验，我们选择了周一至周五作为工作日，其余时间段作为周末。表IV和表V列出了四种方法在NYC-Bike、NYC-Taxi和TaxiBJ数据集上在高峰与非高峰以及工作日与周末的预测结果。可以看出，在高峰期，MUSE-Net在TaxiBJ数据集上的表现略逊于ST-SSL，可能的原因是ST-SSL可能通过自监督学习和适当的增强和聚类受益。然而，提出的MUSE-Net在高峰与非高峰和工作日与周末的比较中，在RMSE上获得了0.77%至21.63%的增益和4.14%至24.66%的RMSE增益，分别证明了MUSE-Net的稳健性。

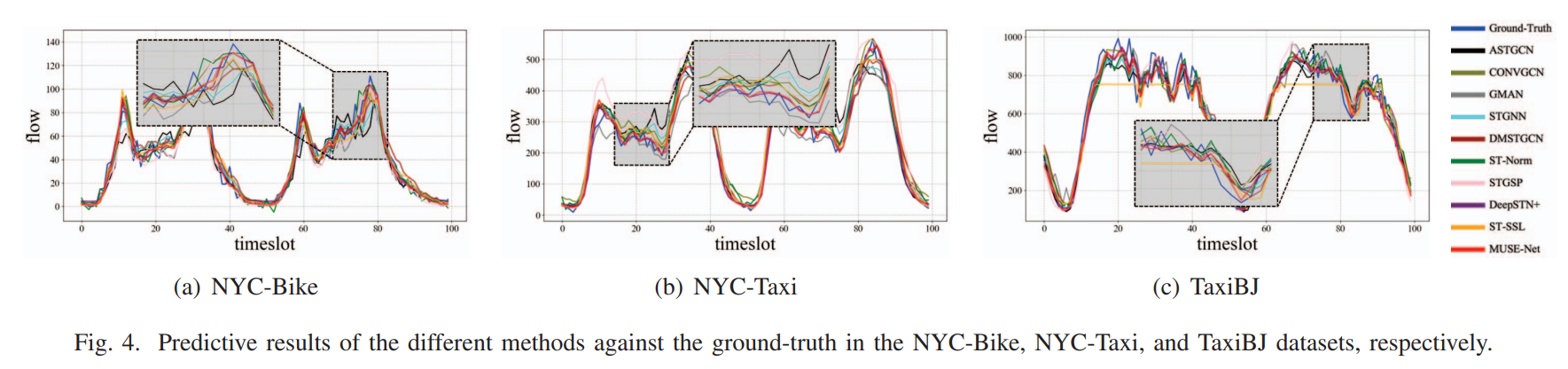
为了进一步评估我们提出的MUSE-Net的有效性，我们在NYC-Bike、NYC-Taxi和TaxiBJ数据集中展示了不同方法与真实数据的预测比较，如图4所示。我们可以观察到，提出的MUSE-Net不仅在非高峰期准确拟合了真实曲线，还在高峰期更好地建模了真实曲线的动态变化。这些结果表明了所提出方法在交通预测中优于基线方法的优势。

D. 消融研究 (RQ 2)

为了评估所提出的MUSE-Net各组件的有效性和贡献，我们在三个基准数据集上通过实施MUSE-Net的四个变体进行对比消融研究：

• MUSE-Net-w/o-Spatial：从我们的模型中删除空间模块（即无ResPlus网络的模型）
• MUSE-Net-w/o-MultiDisentangle：使用跨变量解缠替代多变量解缠；即，我们学习三个不同的交互表示，这些表示在任意配对的时间子序列中共享信息，例如$Z^{CP}$在$C$和$P$之间共享信息，而不是$Z^S$在所有时间子序列中共享信息。
• MUSE-Net-w/o-SemanticPushing：从我们的模型中删除语义推动模块（即没有Eq. (9)的整体目标函数）
• MUSE-Net-w/o-SemanticPulling：从我们的模型中删除语义拉取模块（即没有Eq. (16)的整体目标函数）

表VI 列出了在NYC-Bike、NYC-Taxi和TaxiBJ数据集上与原始MUSE-Net相比的消融实验结果。

可以看出，我们提出的MUSE-Net显然比其消融变体取得了更好的结果，表明了MUSE-Net各部分的有效性。此外，我们可以得出以下观察结论。首先，MUSE-Net-w/o-Spatial表现最差，与MUSE-Net相比，性能下降了7%至35%，这表明空间依赖性在交通流预测中的重要性。在删除了空间模块后，我们的MUSE-Net（可以被视为仅考虑时间的模型）仍然在三个数据集上与空间-时间方法（如STGSP、STGNN和GMAN）竞争，验证了我们提出的交通流预测解缠方法的有效性。其次，MUSE-Net-w/o-MultiDisentangle表现第二差，与MUSE-Net相比，性能下降了4%至13%。通过使用多变量解缠模块，所提出的MUSE-Net能够直接将公共模式从存在于每个时间子序列中的私人模式中分离出来。结果，MUSE-Net在捕捉交通流的多周期性方面表现得更加出色。第三，正则化项，包括语义推动和语义拉取，由于它们在使所学到的专属和交互表示独立和信息性方面的优势，可以稳定地提高交通流预测。

E. 解缠的独立性分析 (RQ 3)

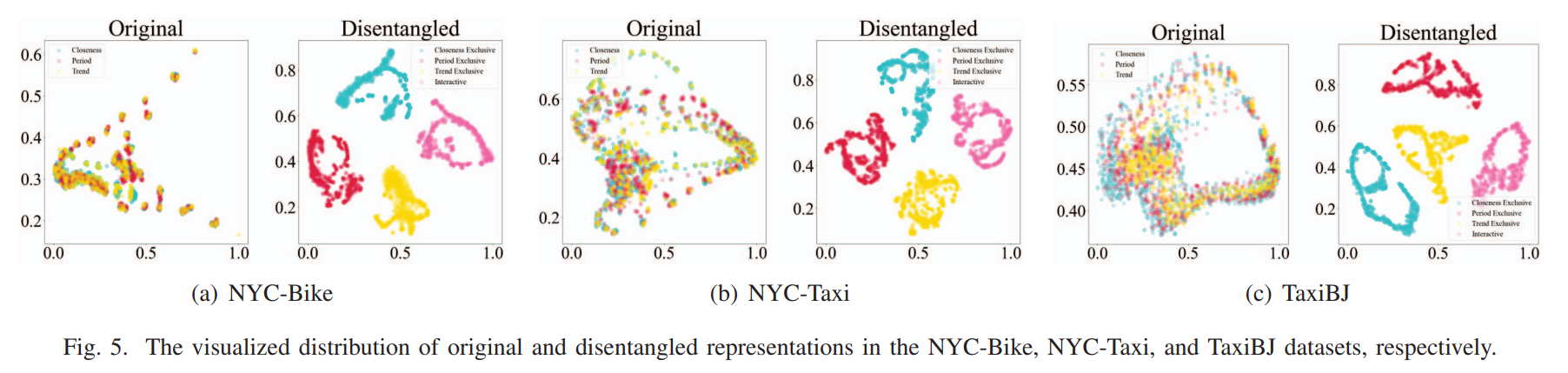
MUSE-Net不仅试图将多周期性模式解缠为专属和交互表示，而且还通过语义推动正则化保持每个表示与其他表示的独立性。为了验证解缠的独立性，我们通过比较原始数据与解缠表示的2D分布可视化进行实验。具体来说，我们首先从原始多时间子序列（即紧密度、周期和趋势子序列）中学习到解缠表示（即三个专属表示和一个交互表示），然后通过t-SNE将原始数据和解缠表示同时投射到2D分布中。通过这种方式，我们可以通过识别不同表示的聚类来验证独立性。图5可视化了原始数据和解缠表示的2D分布。显然，不同时间子序列的原始数据混合在一起，表明了多个原始时间子序列之间的纠缠。相反，每个解缠表示与其他表示分开，鼓励在不同时间维度中捕获特定模式。这验证了我们提出的方法可以有效地从交通流中解缠多周期性模式，并确保每种模式的独立性。

F. 解缠的信息量分析 (RQ 4)

尽管MUSE-Net可以将多周期性模式解缠为专属和交互表示，但这些表示是否提供了足够的信息进行交通流预测？在此，我们进行相似性分析以评估在TaxiBJ数据集上的解缠表示的信息量。具体来说，我们首先计算配对表示之间的余弦相似性，然后通过热图可视化相似性矩阵。相似性值范围从-1到1，可以描述一个表示为另一个表示提供了多少信息。值越高，提供的信息就越多。

我们首先进行相似性分析，以评估交互表示从紧密度、周期和趋势子序列中学习了多少信息。为此，我们计算并描绘了交互表示相对于原始紧密度、周期和趋势子序列的相似性，如图6所示。显然，三个热图中的大多数点都大于零，这表明交互表示可以从紧密度、周期和趋势子序列中学习到足够有用的信息。这验证了我们提出的语义拉取正则化在将交互表示拉向原始多个时间子序列方面的有效性。

此外，我们还进行了另一种相似性分析，以评估专属和交互表示如何对预测作出贡献。因此，我们计算并可视化了专属和交互表示与未来交通流的相似性。如图7所示，交互表示的颜色（即相似性分布）与专属表示相反。这表明交互表示的信息与专属表示的信息是互补的。因此，专属和交互表示的结合可以提供足够的信息来准确预测未来的交通流。

G. 可解释性分析（RQ 5）

由于解缠方法提供了解释学习的能力，我们进一步评估并展示了解缠后的专属表示和互动表示的含义。具体来说，我们计算解缠表示与未来交通流之间的相似度矩阵。矩阵的对角线代表时刻 $t$ 的未来交通流与对应表示之间的相似度。相似度的取值范围从 $-1$ 到 $1$。值越大，解缠表示与未来交通流的相似度越高。

图 8 展示了 TaxiBJ 数据集中某个区域的交通流示例（区域 (5, 4)）。该交通流数据采集自 2013 年 11 月 10 日 18:30 到 2013 年 12 月 10 日 09:30，该时间段可分为高峰时段（即 18:30 - 23:00 和 07:00 - 09:30）和非高峰时段（即 23:00 - 06:30）。

可以看出，三个专属表示在高峰时段的相似度值大于零，而在非高峰时段的相似度值小于零。此观察表明，专属表示揭示了高峰时段的交通模式。这可能的原因是专属表示能够有效地表征特有属性，能够在波动的交通流中建模独特的数据分布。此外，我们注意到在非高峰时段，互动表示的相似度值大于高峰时段，这表明互动表示揭示了非高峰时段的交通模式。可能的原因是互动表示设计用于捕捉共享相似数据分布的常见模式。因此，互动表示能够更好地建模正常分布的交通流，如非高峰时段的交通流。

H. 参数敏感性分析（RQ 6）

所提出的 MUSE-Net 主要包含三个参数，即权衡参数 $\lambda$、采样维度 $k$ 和表示维度 $d$。为了评估这三个参数，我们首先从候选集合 { 1 0 − 3 ∼ 1 0 3 } \{10^{-3} \sim 10^3\} {10−3∼103}、 { 16 ∼ 1024 } \{16 \sim 1024\} {16∼1024} 和 { 16 ∼ 320 } \{16 \sim 320\} {16∼320} 中设置 $\lambda$、$k$ 和 $d$。然后，我们重复实验十次并将平均结果作为实验结果，以比较这些参数对 MUSE-Net 的影响。图 9 展示了 MUSE-Net 在 NYC-Bike 数据集上，不同参数值与 RMSE 值之间的关系，其中蓝色曲线表示平均结果，浅蓝色背景表示结果的波动范围。

正如图 9(a) 所示，当 $\lambda$ 远大于或远小于 1 时，预测性能变得不稳定。这是因为 $\lambda$ 平衡了由互动表示捕获的信息量与专属表示的信息量之间的权衡。当 $\lambda$ 增加时，MUSE-Net 学习到的信息量有限。当 $\lambda$ 减少时，MUSE-Net 学习到冗余信息。因此，我们通过实验将 $\lambda$ 设置为 1 以获得最佳性能。从图 9(b) 可以看出，MUSE-Net 可以在广泛的 $k$ 范围内实现具有可比性的预测性能。可能的原因是小维度的均值和标准差已足以表示表示分布，并评估不同表示之间的差异。因此，我们经验上将 $k=128$ 设为所有数据集的最佳性能值。从图 9© 中可以看出，所提出的方法对参数 $d$ 不敏感，并且表示维度的不同值可以实现具有竞争力的性能。因此，我们选择性能最佳的参数作为表示维度，即 $d=64$。

VI. 结论

在这项工作中，我们通过提出一种新颖的解缠框架，即 MUSE-Net，来缓解分布偏移和互动偏移问题，从而研究了交通流预测。特别是，我们的 MUSE-Net 不仅可以处理多变量解缠问题，还鼓励解缠表示是独立和信息丰富的。此外，我们推导出一个下界估计器，以直接区分和优化解缠问题。综合实验结果验证了 MUSE-Net 在解缠方面的有效性，并证明了 MUSE-Net 相比最先进的交通流预测方法的优越性。

在将数据传感器映射到基于坐标的网格并将数据截取为接近度、周期和趋势系列之后，我们可以轻松地将所提出的方法应用于其他预测应用，如人口级别流行病预测、空气质量预测和能源预测。考虑到多周期学习中解缠的强大能力，我们相信所提出的 MUSE-Net 在多种预测应用中都可以发挥作用。