有限自动机DFA 、 无限自动机NFA

 有限自动机：是一种识别装置的抽象概念，它能准确的识别正规集。

分为确定的有限自动机 简称有限自动机DFA、不确定的有限自动机简称无限自动机NFA。

其实DFA  是NFA的特例

确定的有限自动机和不确定的有限自动机的判断：
就是看关于该结点的路径相同数字是否到达不同的结点，如果相同数字不同结点就是不确定的有限自动机。

一个有限自动机所识别的语言是从开始状态到终止状态所有路径上的字符串的集合。要判断一个字符串能否被指定的自动机识别，就看在该自动机的状态图中能否找到一条从开始状态到达终止状态的路径，且路径上的字符串等于需要识别的字符串

1，确定的有限自动机DFA：

一个DFA可以用两个直观的方式表示：状态转换图、状态转换矩阵。

状态转换图是一个有向图，简称转换图。例如：（s0为初态、s3为终态）

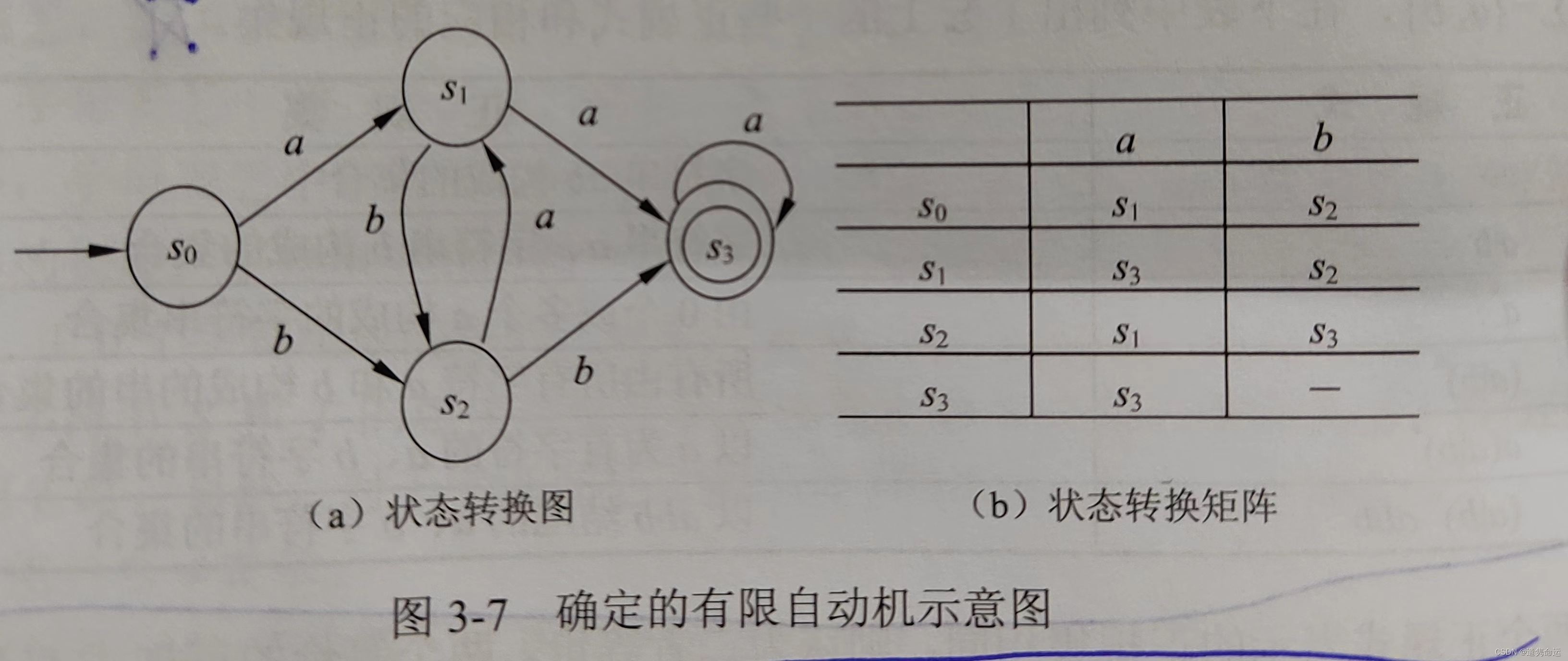
 确定的有限自动机能识别的语言是能够从初态到终态的标记串。例如上图的aaa、aaaa是能够识别的有限自动机语言。

2，不确定的有限自动机NFA：

例1：下图所示的有限自动机中，s0是初始状态，s3为终止状态，该自动机不能识别（A）。

A．abab        B．aaaa       C．babb          C．abba

问题解析：

对于字符串“abab”，其识别路径为s0→s1→s2→s1→s2，字符串结束时的状态不是终止状态，所以该自动机不能识别“abab”。

对于字符串“aaaa”，其识别路径为s0→s1→s3→s3→s3，字符串结束时的状态是终止状态，所以该自动机可以识别“aaaa”。

对于字符串“babb”，其识别路径为s0→s2→s1→s2→s3，字符串结束时的状态是终止状态，所以该自动机可以识别“babb”。

对于字符串“abba”，其识别路径为s0→s1→s2→s3→s3，字符串结束时的状态是终止状态，所以该自动机可以识别“abba”。

例2 、有限自动机DFA

起点到终态0---4，有两条路，aa或者bb，这样排除B、D，最后一个是b，所以排除C,最后选择A