Levenberg-Marquardt算法

L~M方法：

L~M（Levenberg-Marquardt）方法有些让人摸不清头脑。玉米觉得L~M让人困扰的主要原因有两点：一是L~M从何而来、二是L~M怎么样用？因为玉米也不是研究最优化理论的，所以玉米在这里用较为通俗的观点，为大家分析一下L~M方法。在数学上的不严谨之处，期望大家海涵。

一、L~M从何而来

首先，L~M方法首先是一种非线性规划方法；其次其主要用于无约束的多维非线性规划问题；最后，它是一阶牛顿法的一种改进，改进的目的是为了更快的收敛。

既然如此，那么让我们先来了解一下L~M方法的“前辈”一阶牛顿法吧。对一阶牛顿法的理解会帮助我们了解L~M方法的总体思路。

         对于无约束的多维非线性规划问题，起码我们需要一个可以令人接受的参数估计的初始解，我们设其为：X^k。（举个例子，这就是张正友标定法中通过纯粹的几何推导得出的摄像机参数）。在X^k的基础上，我们去寻找比X^k更“靠谱”的估计值。既然我们已经认为X_k可以令人接受，那么更好更精确的估计值应该在X_k的附近，在距离X_k长度为Δ^k的地方。那么，现在我们用一点点高等数学的知识：泰勒展开式。对于一阶牛顿法，我们用一阶泰勒展式逼近X^k附近点的f(X_k+Δ^k)估计值。（这里提到的量都是矩阵形式哦比如，在张正友标定法中f(X_k+Δ^k)由u和v组成）如下

        假设ε=X^k+1-X^k在某时以变化的缓慢到我们认为算法以收敛。我们称ε为终止条件。

        那么，我们就这样迭代下去，总会得到符合我们预期的X^k+1。

        以上就是一阶牛顿法，说白了就是一个不断向着有利方向迭代的过程。

        L~M方法是在一阶牛顿法基础上的改进。为加快收敛，L~M把上面的正规化方程改成了增量正规化方程。如下：

         λ就是增量方程中所谓的增量。

         L~M方法中，取增量的规则如下：

         最初，设λ=0.0001，如果增量方程的解Δ^k导致e^k减小，我们就接受这个λ，并在下一次迭代中使用λ/10代换λ。如果λ值对应的增量方程的解Δ^k导致e^k增大，我们就舍弃这个λ，并将其代换为10λ重解增量方程。循环往复直到e^k下降为止。λ^k+1=10λ^k

         L~M也是迭代循环，直到总会得到符合我们预期的X^k+1为止。

        以上就是L~M方法的原理与出处。大家一定觉得昏昏欲睡了。那么下一部分，应该是大家喜闻乐见的。玉米，将L~M算法的过程总结成算法流程图，与大家分享。||Δ^k||<ε

二、L~M这样用：

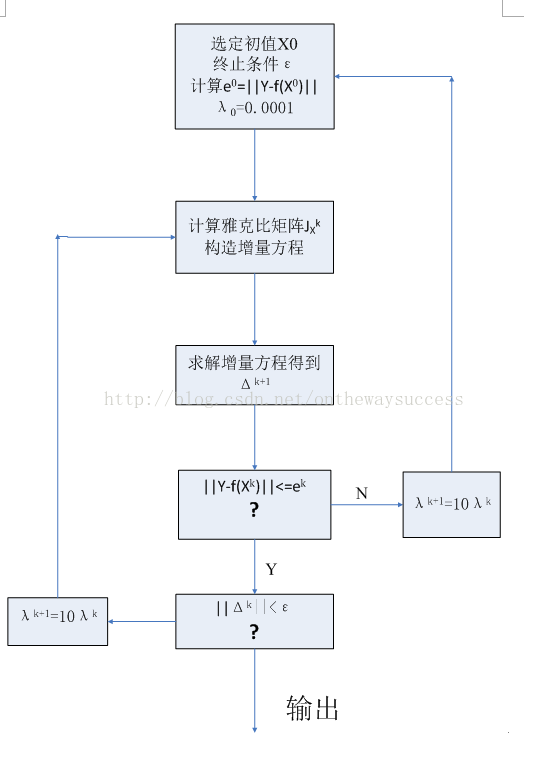
         该流程图就是L-M算法的算法流程。玉米就不多说什么了，流程图更清晰一些。

什么是最优化，可分为几大类？
答：Levenberg-Marquardt算法是最优化算法中的一种。最优化是寻找使得函数值最小的参数向量。它的应用领域非常广泛，如：经济学、管理优化、网络分析、最优设计、机械或电子设计等等。
根据求导数的方法，可分为2大类。第一类，若f具有解析函数形式，知道x后求导数速度快。第二类，使用数值差分来求导数。
根据 使用模型不同，分为非约束最优化、约束最优化、最小二乘最优化。

什么是Levenberg-Marquardt算法？
它是使用最广泛的非线性最小二乘算法，中文为列文伯格-马夸尔特法。它是利用梯度求最大（小）值的算法，形象的说，属于“爬山”法的一种。它同时具有梯度法和牛顿法的优点。当λ很小时，步长等于牛顿法步长，当λ很大时，步长约等于梯度下降法的步长。在作者的科研项目中曾经使用过多次。图1显示了算法从起点，根据函数梯度信息，不断爬升直到最高点（最大值）的迭代过程。共进行了12步。（备注：图1中绿色线条为迭代过程）。

 

图1 LM算法迭代过程形象描述

图1中，算法从山脚开始不断迭代。可以看到，它的寻优速度是比较快的，在山腰部分直接利用梯度大幅度提升（参见后文例子程序中lamda较小时），快到山顶时经过几次尝试（lamda较大时），最后达到顶峰（最大值点），算法终止。

 

如何快速学习LM算法？

学 习该算法的主要困难是入门难。 要么国内中文教材太艰涩难懂，要么太抽象例子太少。目前，我看到的最好的英文入门教程是K. Madsen等人的《Methods for non-linear least squares problems》本来想把原文翻译一下，贴到这里。请让我偷个懒吧。能找到这里的读者，应该都是E文好手，我翻译得不清不楚，反而事倍功半了。

可在 下面的链接中找到
http://www2.imm.dtu.dk/pubdb/public/publications.php? year=&pubtype=7&pubsubtype=&section=1&cmd=full_view&lastndays=&order=author
或者直接下载pdf原文：
http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/3215/pdf/imm3215.pdf

 

   LM算法是介于牛顿法与梯度下降法之间的一种非线性优化方法，对于过参数化问题不敏感，能有效处理冗余参数问题，使代价函数陷入局部极小值的机会大大减小，这些特性使得LM算法在计算机视觉等领域得到广泛应用。

算法流程

          

 在LM算法中，每次迭代是寻找一个合适的阻尼因子λ，当λ很小时，算法就变成了GAuss-Newton法的最优步长计算式，λ很大时，蜕化为梯度下降法的最优步长计算式。

参考文献：

[1]. 张鸿燕， 狄征. Levenberg-Marquardt算法的一种新解释. 计算机工程与应用，2009，45(19),5-8.

from： http://heleiying.blog.163.com/blog/static/3110429201081693815164/

Levenberg-Marquardt快速入门教程（荐）
例子程序（MATLAB源程序）
本程序不到100行，实现了求雅克比矩阵的解析解，Levenberg-Marquardt最优化迭代，演示了如何求解拟合问题。采用萧树铁主编的《数学试验》（第二版）（高等教育出版社）中p190例2（血药浓度）来演示。在MATLAB中可直接运行得到最优解。

 

*************************************************************************

% 计算函数f的雅克比矩阵，是解析式
syms a b y x real;
f=a*exp(-b*x);
Jsym=jacobian(f,[a b])

% 拟合用数据。参见《数学试验》，p190，例2
data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
obs_1=[19.21 18.15 15.36 14.10 12.89 9.32 7.45 5.24 3.01];

% 2. LM算法
% 初始猜测s
a0=10; b0=0.5;
y_init = a0*exp(-b0*data_1);
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=2;
% 迭代最大次数
n_iters=50;
% LM算法的阻尼系数初值
lamda=0.01;

% step1: 变量赋值
updateJ=1;
a_est=a0;
b_est=b0;

% step2: 迭代
for it=1:n_iters
    if updateJ==1
        % 根据当前估计值，计算雅克比矩阵
        J=zeros(Ndata,Nparams);
        for i=1:length(data_1)
            J(i,:)=[exp(-b_est*data_1(i)) -a_est*data_1(i)*exp(-b_est*data_1(i))];
        end
        % 根据当前参数，得到函数值
        y_est = a_est*exp(-b_est*data_1);
        % 计算误差
        d=obs_1-y_est;
        % 计算（拟）海塞矩阵
        H=J'*J;
        % 若是第一次迭代，计算误差
        if it==1
            e=dot(d,d);
        end
    end

    % 根据阻尼系数lamda混合得到H矩阵
    H_lm=H+(lamda*eye(Nparams,Nparams));
    % 计算步长dp，并根据步长计算新的可能的\参数估计值
    dp=inv(H_lm)*(J'*d(:));
    g = J'*d(:);
    a_lm=a_est+dp(1);
    b_lm=b_est+dp(2);
    % 计算新的可能估计值对应的y和计算残差e
    y_est_lm = a_lm*exp(-b_lm*data_1);
    d_lm=obs_1-y_est_lm;
    e_lm=dot(d_lm,d_lm);
    % 根据误差，决定如何更新参数和阻尼系数
    if e_lm        lamda=lamda/10;
        a_est=a_lm;
        b_est=b_lm;
        e=e_lm;
        disp(e);
        updateJ=1;
    else
        updateJ=0;
        lamda=lamda*10;
    end
end
%显示优化的结果
a_est
b_est

************************************************************

转自：http://www.shenlejun.cn/my/article/show.asp?id=17&page=2