TIM阅读笔记

TIM阅读笔记

Boudiaf M, Masud Z I, Rony J, et al. Transductive information maximization for few-shot learning[J]. arXiv preprint arXiv:2008.11297, 2020.

昨天下午出去蹦跶去了，今天来赶工。今天这篇论文是 NeurIPS 2020 的一个工作，乍一看还是一个Tim？腾讯的那个？不是哈哈哈，Transductive Information Maximization For Few-Shot Learning，这篇文章上周看的时候脑子基本上就是蒙的，很多东西都忘了，下来补了一下信息论基础和前天那篇先验工作才能勉强看懂，可能有很多不足的地方，欢迎大佬指正啊。

一些pre-knowledge

Transductive Learning

这个其实我都不知道怎么翻译，这方面的工作近两年在FSL领域比较火，明天会出一篇这个相关的paper，这里简单的介绍一下，注意不要把这个和半监督学习搞混了。

监督学习中的train和test集是不交叉的，这种叫做inductive learning。
半监督学习中我们添加了额外的未标记数据辅助训练，它的train和test集依然是不交叉的，叫做inductive semi-supervise learning。
假设我们添加的这部分未标注的数据部分或者全部来自test set，那么这时候很明显train和test就相交了，这种叫做transductive learning。

文章主要思想

这篇文章其实就是上一篇文章在FSL领域的一次应用，这篇文章也是希望通过最大化输入和输出之间的互信息，这里的输入指的是embed后的query feature，输出指的是label，这个前天那篇文章提到的思想很相似。作者采用了交替方向乘子法solver（ alternating-direction solver ，不知道怎么翻译）来加速推理，也能够提升精度。

Details

这里author还是采用了两阶段metrics learning的方式来做，首先是一个feature extractor：$f_{\varphi }:\mathcal{X}⟶\mathcal{Z}\subset {\mathbb{R}}^d$，作者对这个特征向量$\mathcal{Z}$也做了normalization：${\mathbf{z}}_i=\frac{f_{\mathbf{\varphi }}\left({\mathbf{x}}_i\right)}{{\Vert f_{\mathbf{\varphi }}\left({\mathbf{x}}_i\right)\Vert }_2}$，对于分类器作者直接选择了一个soft分类器，直接将利用一个权重矩阵对输出特征进行映射，那么对于第i个样本标签为k的概率分布就为：$p_{ik}:=\mathbb{P}\left(Y=k\mid X={\mathbf{x}}_i;\mathbf{W},\mathbf{\varphi }\right)$。中间变量$\mathcal{Z}$是一个d维的向量，$p_{ik}$表示第i个样本为标签k的概率，那么在权重分类上就相当于是特征向量$\mathcal{Z}$乘以对应第k个权重向量$w_k$，那么$p_{ik}\propto \exp \left(-\frac{\tau }{2}{\Vert {\mathbf{w}}_k-{\mathbf{z}}_i\Vert }^2\right)$，其中这个$\tau$是一个温度参数，那么$p_{i k} $在queryset上的边缘分布为$\widehat{p}{k}=\frac{1}{|\mathcal{Q}|} \sum\limits{ i \in \mathcal{Q}} p_{i k}$，

按照我们的目标就是最大化这个输入输出之间的互信息，作者将它定义为下面所示的样子：
$${\hat{\mathcal{I}}}_{\alpha }\left(X_{\mathcal{Q}};Y_{\mathcal{Q}}\right):=\underset{\hat{\mathcal{H}}\left(Y_{\mathcal{Q}}\right):\text{ marginal entropy }}{\underbrace{-\sum _{k=1}^K{\hat{p}}_k\log {\hat{p}}_k}}+\alpha \underset{-\hat{\mathcal{H}}\left(Y_{\mathcal{Q}}\mid X_{\mathcal{Q}}\right):\text{ conditional entropy }}{\underbrace{\frac{1}{|\mathcal{Q}|}\sum _{i\in \mathcal{Q}}\sum _{k=1}^K{p}_{ik}\log \left(p_{ik}\right)}}$$

这是不是认不到为什么这样设计？？？这就是前面我们的互信息啊，前面是$\hat{H}(Y_Q)$，后面是$\hat{H}(Y_Q|X_Q)$，这一部分是$P(Y_Q|X_Q)$条件熵，熵是不确定性的期望。熵越大，变量的不确定性越大，也就是说我们要最小化query set中无标签数据的后验概率，从数学公式上讲，被减数不变，减数减小了，差肯定变大。去年的ICLR上也有一片类似的工作就单独只用了这一部分作为损失函数，这一部分很重要。由互信息的定义可得，这两者的差就是互信息。作者加了一个正则项$\alpha$，如果$\alpha =1$就是原本的互信息。

但是你发现没，即使到这个时候我们也只是利用了query set的信息，别忘了FSL本质上还是Supervised learning，support set仍然可以提供监督信息，于是在loss中还添加了一个CE来保证监督信息的编码，我们需要最小化CE，最大化互信息，为了保证训练的一致性，我们把互信息作相反数，与CE相加。

作者选用的特征提取板块是预训练的模型，除了使用梯度下降，作者还提出了一种优化方案ADMM，作者提出这种方案能过够极大程度提高模型的速度。思路是在原始的loss上加了一个正则项，就是p，q的KL散度，即当前的损失函数就变成了：

$$\underset{\mathbf{W},\mathbf{q}}{\min }\underset{\mathrm{C}\mathrm{E}}{\underbrace{-\frac{\lambda }{|\mathcal{S}|}\sum _{i\in \mathcal{S}}\sum _{k=1}^K{y}_{ik}\log \left(p_{ik}\right)}}+\underset{\sim \hat{\mathcal{H}}\left(Y_{\mathcal{Q}}\right)}{\underbrace{\sum _{k=1}^K{\hat{q}}_k\log {\hat{q}}_k}}\underset{\sim \hat{\mathcal{H}}\left(Y_{\mathcal{Q}}\mid X_{\mathcal{Q}}\right)}{\underbrace{\frac{\alpha }{|\mathcal{Q}|}\sum _{i\in \mathcal{Q}}\sum _{k=1}^K{q}_{ik}\log \left(p_{ik}\right)}}+\underset{\text{Penalty }\equiv {\mathcal{D}}_{\mathrm{K}\mathrm{L}}(\mathbf{q}\Vert \mathbf{p})}{\underbrace{\frac{1}{|\mathcal{Q}|}\sum _{i\in \mathcal{Q}}\sum _{k=1}^K{q}_{ik}\log \frac{q_{ik}}{p_{ik}}}}$$
当且仅当，$q_{i,k}=p_{i,k}$的时候散度为0，然后ADMM的思路是将这个问题尝试分割成基于W，q的两个子问题，如下所示。作者在论文中给出了形式化的证明，网上也有很多关于ADMM在凸优化领域的介绍，这里不再赘述。
$$\begin{array}{l}{q}_{ik}^{(t+1)}\propto \frac{{\left(p_{ik}^{(t)}\right)}^{1+\alpha }}{{\left({\sum }_{i\in \mathcal{Q}}{\left(p_{ik}^{(t)}\right)}^{1+\alpha }\right)}^{1/2}}\\ {\mathbf{w}}_k^{(t+1)}\leftarrow \frac{\frac{\lambda }{1+\alpha }{\sum }_{i\in \mathcal{S}}\left(y_{ik}{\mathbf{z}}_i+p_{ik}^{(t)}\left({\mathbf{w}}_k^{(t)}-{\mathbf{z}}_i\right)\right)+\frac{|\mathcal{S}|}{|\mathcal{Q}|}{\sum }_{i\in \mathcal{Q}}\left(q_{ik}^{(t+1)}{\mathbf{z}}_i+p_{ik}^{(t)}\left({\mathbf{w}}_k^{(t)}-{\mathbf{z}}_i\right)\right)}{\frac{\lambda }{1+\alpha }{\sum }_{i\in \mathcal{S}}{y}_{ik}+\frac{|\mathcal{S}|}{|\mathcal{Q}|}{\sum }_{i\in \mathcal{Q}}{q}_{ik}^{(t+1)}}\end{array}$$

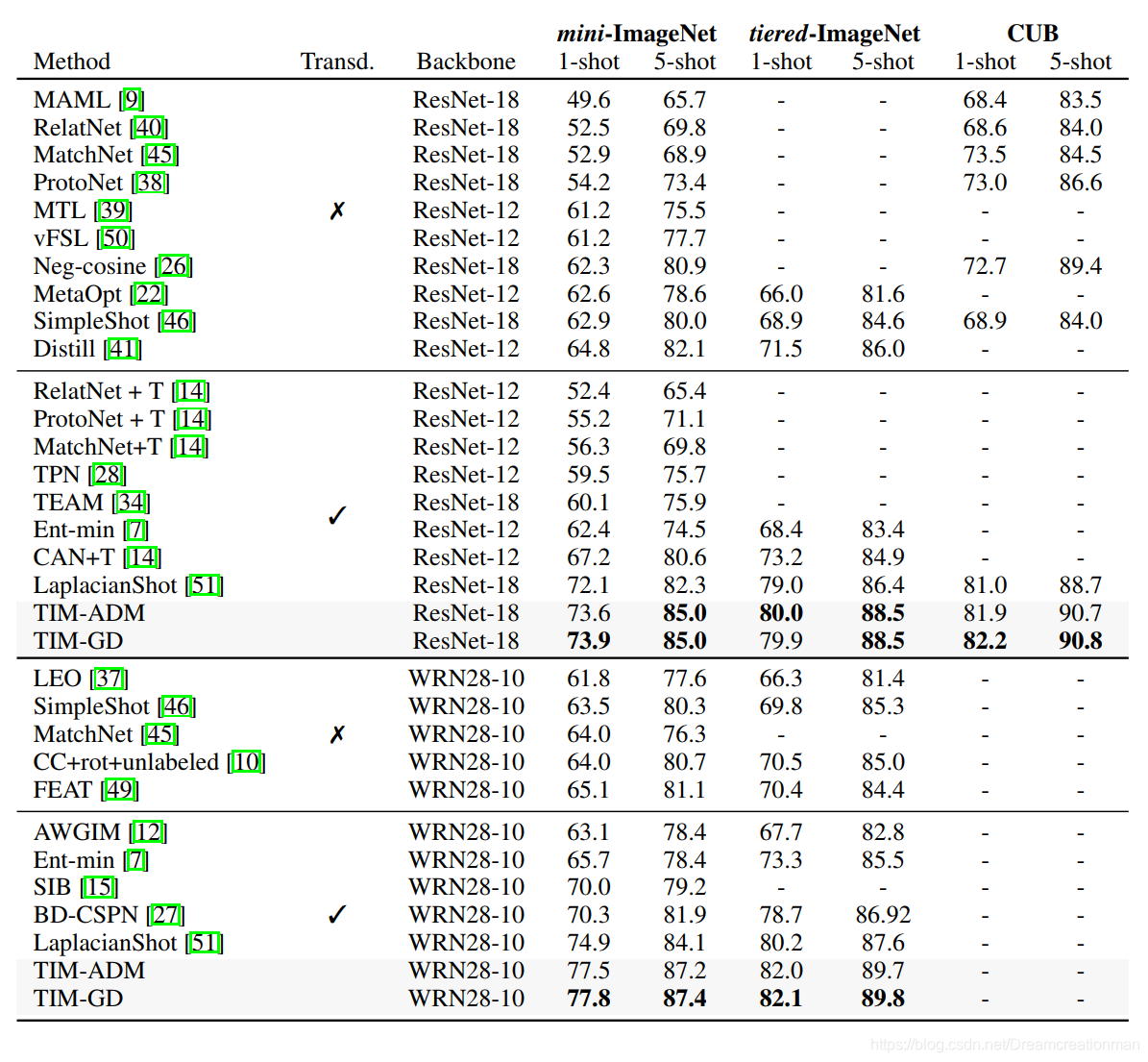
结果

贴一贴实验结果，这是在作者的结果：

后记

如果你觉得我的文章写的不错的话，麻烦帮忙向大家推广关注我的公众号啊（名称：洋可喵）！！！