接着上次的文章“图的构建（邻接链表法）”，邻接链表法构建图相对来说比较简单，并且遍历起来也相对简单，但是要是动态添加图的节点和图的边，则是实在不方便，不过现在不管那么多，今天的主题是遍历。
- 有另外一种图的构建方法，叫做十字链表法，插入删除比较方便，但是相对来说比较复杂，改天闲着木事的再搞。（其实主要原因是因为三四年前写的代码，现在翻出来了，现成的，尼玛现在让我从头写那么复杂的数据结构，死的心都有了，所以还是等哪天心情好了，无聊了再写十字链表吧）
上篇：图的构建（邻接链表法）http://blog.csdn.net/sundong_d/article/details/44983671
本次接着上一篇的讲，图的遍历就是从图中的某一个顶点除法访遍图中的其余顶点，并且使每一个顶点仅被访问一次。图的遍历算法是求解图的连通性问题、拓扑排序和求解关键路径等算法的基础
深度优先遍历
假设一个图，图中的所有顶点都未曾被访问，则深度优先遍历是从图中的某一个顶点v出发，访问此顶点，然后找到与v邻接的并且未被访问的点m出发访问，然后从m的未被访问的邻接点n出发访问，再从那个点n的未被访问的邻接点出发访问，出发......访问......，循环下去，直至图中所有的和v与路径想通的顶点都被访问到；若此时图中还有顶点没有被访问，则另选图中的一个未曾被访问的顶点做起始点，重复上述过程，直到图中的所有顶点都被访问到为止。此处不太好用语言描述，不知道各位看官看明白没有，反正我没糊涂。
下面上个图（截图截人家的，自己懒的画，但是能讲明白就好，黑猫、白猫，逮到耗子就是好猫）：
遍历过程：
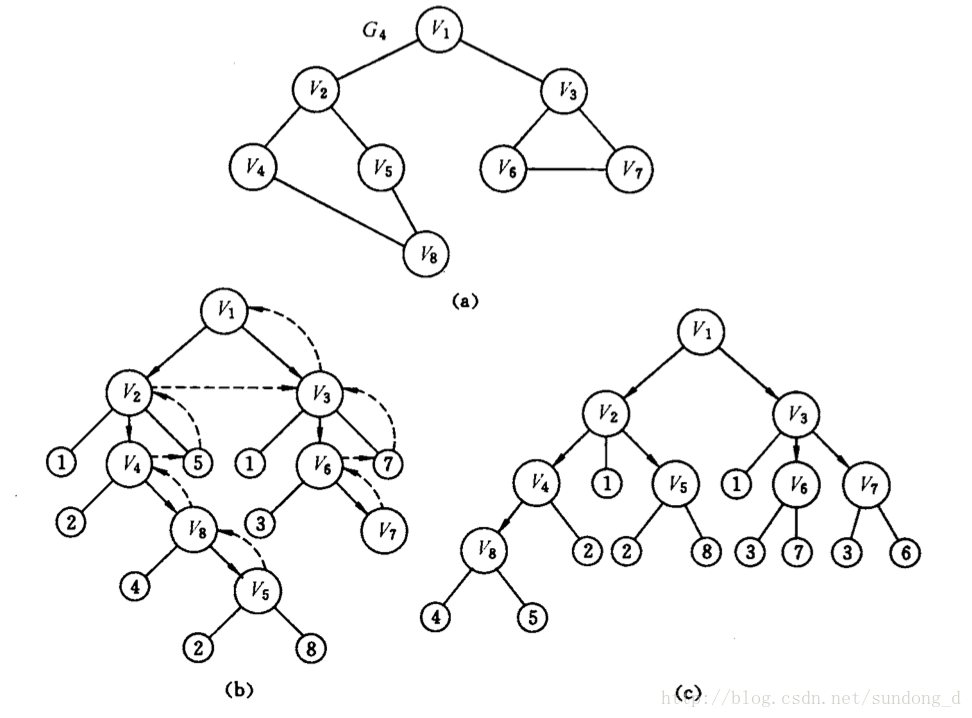
以图(a)中的G4为例，深度优先遍历图的过程如图(b)所示。假设从顶点出发进行搜索，在访问了顶点v1之后，选择邻接点v2。因为v2未曾访问，则从v2出发进行搜索，以此类推，接着从v4，v8，v5出发尽心搜索。在访问了v5之后，由于v5的邻接点都被访问，则回到v8。然后......就这样一直回到v1，然后又从v1搜索v3，如此进行下去。由此的发哦的访问序列为：
v1-->v2-->v4-->v8-->v5-->v3-->v6-->v7
当然，也可以在首先访问图中任何一个点，那样就会有不通过的访问序列。
注：图(c)是广度优先遍历的示意图。
接下来是代码，C++实现，其实也可以用其他语言写，道理都是想通的，只不过实现的方式不同
bool visited[MAX_VERTEX_NUM];
int FirstAdjVex(ALGraph &G,int v)
{
int i;
int n=-1;
ArcNode*p;
p=G.vertices[v].firstarc;
if(p)
{
i=p->adjvex;
if(visited[i]==false)
n=i;
}
return n;
}
int NextAdjVex(ALGraph &G,int v)
{
int i;
int n=-1;
ArcNode *p;
p=G.vertices[v].firstarc;
for(i=p->adjvex;i<G.vexnum,p!=NULL;)
{
i=p->adjvex;
if(visited[i]==false)
{
n=i;
break;
}
else
p=p->nextarc;
}
return n;
}
void VisitFuc(ALGraph &G,int v)
{
cout<<G.vertices[v].date<<" ";
}
void DFS(ALGraph &G,int v)
{
int w;
visited[v]=true;
VisitFuc(G,v);
for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v))
if(!visited[w]) DFS(G,w);
}
void DFSTraverse(ALGraph &G)
{
int v;
for(v=0;v<G.vexnum;v++)
visited[v]=false;
cout<<"深度优先搜索："<<endl;
for(v=0;v<G.vexnum;v++)
{
if(!visited[v])
DFS(G,v);
}
}
广度优先遍历
广度优先遍历是按照图的层次结构遍历的过程。
简单理解就是访问图中的一个点之后，一次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发，依次访问它们的邻接点，并且使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。就像向湖面投一粒石子，激起一层的波纹。我们访问一个点，先把这个点的所有未被访问的邻接点依次全部访问，然后再在已经访问的的邻接点中找到那个最早被访问的点，从这个点出发，访问这个点所有未被访问的邻接点，如此循环下去。
如图(c)(此图在上面深度优先遍历的那个图里面)，是对图G4进行广度优先遍历。沙鸥县访问v1和v1的邻接点v2和v3，然后依次访问v2的邻接点v4和v5及v3的邻接点v6和v7，最后访问v4的邻接点v8。由于这些顶点的邻接点均已经被访问，并且图中所有顶点都被访问，由此完成了图的遍历。
顶点访问序列：v1-->v2-->v3-->v4-->v5-->v6-->v7-->v8
和深度优先遍历类似，我们在遍历过程中需要一个访问标志数组。并且，为了顺序访问路径长度为2、3、...的顶点，需要附设队列以存储已经被访问的路径长度为1，2...的顶点。
上代码：
void BFSTraverse(ALGraph &G)
{
int v;
int w;
queue<int> q;
for(v=0;v<G.vexnum;v++)
visited[v]=false;
cout<<"广度优先搜索：";
for(v=0;v<G.vexnum;v++)
{
if(!visited[v])
{
visited[v]=true;
VisitFuc(G,v);
q.push(v);
while(q.empty()!=true)
{
v = q.front();
q.pop();
for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v))
{ if(!visited[w])
{
visited[w]=true;
VisitFuc(G,w);
q.push(w);
}
}
}
}
}
}
好了，图的两种遍历方法讲完了，下面贴上整个工程的代码，代码中是没有这么多注释的，当有看不懂的时候，参考上一篇博客和本篇博客中对程序的注释
#include<iostream>
#include<string>
#include<queue>
using namespace std;
#define ERROR 1
#define MAX_VERTEX_NUM 100
typedef struct ArcNode{
int adjvex;
struct ArcNode *nextarc;
string info;
}ArcNode;
typedef struct VNode{
char date;
ArcNode * firstarc;
}VNode,AdjList[MAX_VERTEX_NUM];
typedef struct{
AdjList vertices;
int vexnum,arcnum;
int kind;
}ALGraph;
int LocateVex(ALGraph &G,char &v1)
{
int i;
for(i=0;i<G.vexnum;i++)
{
if(G.vertices[i].date==v1)
return i;
}
if(i>=G.vexnum)
return ERROR;
else
return 0;
}
void CreateDG(ALGraph &G)
{
ArcNode *p,*q;
char v1,v2;
char v;
int i,j,k,n;
cout<<"请输入图的顶点数和弧数："<<endl;
cin>>G.vexnum;
cin>>G.arcnum;
cout<<"请输入顶点："<<endl;
for(i=0;i<G.vexnum;i++)
{
cin>>v;
G.vertices[i].date=v;
G.vertices[i].firstarc=NULL;
}
cout<<"请输入弧尾和弧头：";
for(k=0;k<G.arcnum;k++)
{
cin>>v1;
cin>>v2;
i=LocateVex(G,v1);j=LocateVex(G,v2);
if(G.vertices[i].firstarc==NULL)
{
p=(ArcNode *)new ArcNode;
G.vertices[i].firstarc=p;
q=G.vertices[i].firstarc;
}
else
{
q=G.vertices[i].firstarc;
for(n=0;n<G.arcnum;n++,q=q->nextarc)
{
if(!q->nextarc)
break;
}
p=(ArcNode *)new ArcNode;
q->nextarc=p;
q=q->nextarc;
}
q->adjvex=j;
q->nextarc=NULL;
}
cout<<"图构建成功！";
}
bool visited[MAX_VERTEX_NUM];
int FirstAdjVex(ALGraph &G,int v)
{
int i;
int n=-1;
ArcNode*p;
p=G.vertices[v].firstarc;
if(p)
{
i=p->adjvex;
if(visited[i]==false)
n=i;
}
return n;
}
int NextAdjVex(ALGraph &G,int v)
{
int i;
int n=-1;
ArcNode *p;
p=G.vertices[v].firstarc;
for(i=p->adjvex;i<G.vexnum,p!=NULL;)
{
i=p->adjvex;
if(visited[i]==false)
{
n=i;
break;
}
else
p=p->nextarc;
}
return n;
}
void VisitFuc(ALGraph &G,int v)
{
cout<<G.vertices[v].date<<" ";
}
void DFS(ALGraph &G,int v)
{
int w;
visited[v]=true;
VisitFuc(G,v);
for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v))
if(!visited[w]) DFS(G,w);
}
void DFSTraverse(ALGraph &G)
{
int v;
for(v=0;v<G.vexnum;v++)
visited[v]=false;
cout<<"深度优先搜索："<<endl;
for(v=0;v<G.vexnum;v++)
{
if(!visited[v])
DFS(G,v);
}
}
void BFSTraverse(ALGraph &G)
{
int v;
int w;
queue<int> q;
for(v=0;v<G.vexnum;v++)
visited[v]=false;
cout<<"广度优先搜索：";
for(v=0;v<G.vexnum;v++)
{
if(!visited[v])
{
visited[v]=true;
VisitFuc(G,v);
q.push(v);
while(q.empty()!=true)
{
v = q.front();
q.pop();
for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v))
{ if(!visited[w])
{
visited[w]=true;
VisitFuc(G,w);
q.push(w);
}
}
}
}
}
}
void menu()
{
cout<<'\n';
cout<<" //---------------图的基本操作---------------//"<<endl;
cout<<" ** 1、图的构建 **"<<endl;
cout<<" ** 2、深度优先遍历 **"<<endl;
cout<<" ** 3、广度优先遍历 **"<<endl;
cout<<" --------------------------------------------"<<endl;
cout<<"请输入数字进行选择："<<endl;
}
int main()
{
ALGraph G;
int i;
menu();
cin>>i;
while(i<4)
{
switch(i)
{
case 1:CreateDG(G);break;
case 2:DFSTraverse(G);cout<<endl;break;
case 3:BFSTraverse(G);cout<<endl;break;
default:return ERROR;
}
menu();
cin>>i;
}
return 0;
}
扫一扫
2963
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
