【Problem】
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
Example 1:
nums1 = [1, 3]
nums2 = [2]
The median is 2.0
Example 2:
nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5
【Thinking】
this is the fourth problem on the leetcode website. The link ishttps://leetcode.com/problems/median-of-two-sorted-arrays/description/. You can try it by yourself.
First time, I used the brute force solution that sort the two arrays into a vector, then find the middle element in the vector. As expected, the complexity over o(log(m+n)). It is not satisfied with the problem requirement. The run time complexity should be o(log(m+n)).
Second time, I choosed to directly find the middle element whentraversal the two array.Using the two
variables---(i,j) to record the position of biggest number between arrays. when i+j==(nums1.length+nums2.length)/2, we find the middle element. We also should consider the nums1.length+nums2.length is odd(奇数) or even number(偶数)to choose different calculate way.
【Important】
Recursive Approach
递归的方法
To solve this problem, we need to understand "What is the use of median". In statistics, the median is used for:
为了解决这个问题, 我们需要理解 “中位数的用途” 。 统计学中,中位数被用于:
Dividing a set into two equal length subsets, that one subset is always greater than the other.
将一个集合分成两个相等长度的子集,一个子集总是比另一个子集大。
If we understand the use of median for dividing, we are very close to the answer.
如果我们理解了中位数在划分时的用途,我们就离答案不远了。
First let's cut A into two parts at a random position i:
首先我们将A以任意位置i切分成两部分:
left_A | right_A
A[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
Since A has m elements, so there are m+1 kinds of cutting (i=0∼m).因为A有m个元素,因此这里有m+1种切法(i=0~m)
And we know:
并且我们知道:
With the same way, cut B into two parts at a random position j:
用同样的方法,在任意位置j上将B切成两部分:
left_B | right_B
B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
Put left_A and left_B into one set, and put right_A and right_B into another set. Let's name them left_part and right_part:将left_A和left_B放入一个集合,并且将right_A 和 right_B 放入另一个集合。我们把它们分别叫做 left_part和 right_part:
left_part | right_part
A[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
If we can ensure:
如果我们可以确定:
- len(left_part)=len(right_part)
- max(left_part)≤min(right_part)
then we divide all elements in {A,B} into two parts with equal length, and one part is always greater than the other. Then
然后我们就可以将{A,B}中所有的元素分成有相同长度的两部分,并且其中的一部分总是比另一部分更大。然后
To ensure these two conditions, we just need to ensure:
为了确保上面的两个条件,我们只需要确保:
-
i+j=m−i+n−j (or: m−i+n−j+1)
if n≥m, we just need to set: i=0∼m, j=m+n+12−i -
B[j−1]≤A[i] and A[i−1]≤B[j]
ps.1 For simplicity, I presume A[i−1],B[j−1],A[i],B[j] are always valid even if i=0, i=m, j=0, or j=n.
ps.1 简单来说,我假设 A[i−1],B[j−1],A[i],B[j] 即使在i=0, i=m, j=0, or j=n 都是有效的。
I will talk about how to deal with these edge values at last.
我将会在最后讨论怎么样去处理这些边界值:
ps.2 Why n≥m? Because I have to make sure j is non-negative since 0≤i≤m and j=2m+n+1−i.
为什么 n≥m? 因为我必须确保 j是一个非负数 当0≤i≤m 和 j=(m+n+1)/2-i
If n<m, then j may be negative, that will lead to wrong result.
如果 n<m, 那么j有可能是负数,那样会导致错误的结果。
So, all we need to do is:
所以,我们所有需要做的事情是:
Searching i in [0,m], to find an object i such that:
找到[0,m]中i的值,用它找到对象i,就像:
B[j−1]≤A[i] and A[i−1]≤B[j], where j=2m+n+1−i
And we can do a binary search following steps described below
并且我们可以跟随下面描述的步骤写一个二分查找
- Set imin=0, imax=m, then start searching in [imin,imax]
2.设置 i=(imin+imax)/2, j=(m+n+1)/2-i
3.Now we have len(left_part)=len(right_part). And there are only 3 situations that we may encounter:
3.现在我们有 len(left_part)=len(right_part). 并且这里我们也许会碰到的情形仅仅只有3种:
一. B[j−1]≤A[i] and A[i−1]≤B[j]
Means we have found the object i, so stop searching.
意味着我们找到了对象 i, 可以停止查找。
二. B[j−1]>A[i]
Means A[i] is too small. We must adjust i to get B[j−1]≤A[i].
意味着 A[i] 太小,我们需要调整 i 去得到 B[j−1]≤A[i].
Can we increase i?
我们能增加 i 吗?
Yes. Because when i is increased, j will be decreased.
是的。因为当 i 增加时, j 将会减少。
So B[j−1] is decreased and A[i] is increased, and B[j−1]≤A[i] maybe satisfied.
因此B[j−1] 减小 并且 A[i] 增大, 这样B[j−1]≤A[i] 也许会满足。
Can we decrease i?
我们能够减小 i 吗?
No! Because when i is decreased, j will be increased.、
不行!因为 当 i 减小时, j 将会被增加。
So B[j−1] is increased and A[i] is decreased, and B[j−1]≤A[i] will be never satisfied.
因此 B[j-1] 将会增加 并且 A[i] 将会减少, 并且 B[j−1]≤A[i] 将永远不会满足。
So we must increase i. That is, we must adjust the searching range to [i+1,imax]..
因此我们必须增加 i .那就是,我们必须调整搜索的范围到 [i+1,imax].
So, set imin=i+1, and goto 2.
所以设置 imin= i+1, 然后跳转到第二步。
三. A[i−1]>B[j]:
Means A[i−1] is too big. And we must decrease i to get i-1 , A[i−1]≤B[j].
意味着 A[i−1] 太大了。并且我们必须减小 i使它 i-1 , A[i−1]≤B[j]
That is, we must adjust the searching range to [imin,i−1]
那就是,我们必须调整寻找范围到[imin,i−1]
So, set imax=i−1, and goto 2.
因此,设置 imax=i-1, 并且转到第二步
When the object i is found, the median is:
当对象 i 找到时,中位数是:
i=0,i=m,j=0,j=n where A[i−1],B[j−1],A[i],B[j] may not exist.
i=0,i=m,j=0,j=n的时候A[i−1],B[j−1],A[i],B[j] 也许不会存在。
Actually this situation is easier than you think.
事实上这个情形比你想象得要简单。
What we need to do is ensuring that max(left_part)≤min(right_part). So, if i and j are not edges values (means
我们需要做的就是确保 max(left_part)≤min(right_part). 因此,如果i 和j 不是边缘值(意味着
A[i−1],B[j−1],A[i],B[j] all exist), then we must check both B[j−1]≤A[i] and
A[i−1],B[j−1],A[i],B[j] 都存在,我们必须检查 B[j−1]≤A[i]和
A[i−1]≤B[j]. But if some of A[i−1],B[j−1],A[i],B[j] don't exist,
A[i−1]≤B[j]。但是如果其中一些A[i−1],B[j−1],A[i],B[j] 不存在的话
then we don't need to check one (or both) of these two conditions.
然后我们不需要检查两个条件中的其中一个或者全部。
For example, if i=0, then A[i−1] doesn't exist, then we don't need to check A[i−1]≤B[j]. So, what we need to do is:
举个例子,如果 i=0, 然后 A[i−1] 不存在,我们就不需要检测A[i−1]≤B[j]。 因此,我们需要做的事情就是:
Searching i in [0,m], to find an object i such that:
找到在 [0,m] 中的 i ,找到对象 i 就像:
(j=0 or i=m or B[j−1]≤A[i]) and
(j=0 or i=m or B[j−1]≤A[i])并且
(i=0 or j=n or A[i−1]≤B[j]), where j=2m+n+1−i
Thanks to @Quentin.chen for pointing out that: i<m⟹j>0 and i>0⟹j<n . Because:
多谢@Quentin.chen 指出:i<m⟹j>0 和 i>0⟹j<n 因为:
i>0⟹j<ni>0⟹j<n
i>0⟹j<n
(我感觉最后一个不等式应该是<=n+(1/2),不过也不影响)
java 代码
class Solution {
public double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length;
int n = B.length;
if (m > n) { // to ensure m<=n
int[] temp = A; A = B; B = temp;
int tmp = m; m = n; n = tmp;
}
int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
while (iMin <= iMax) {
int i = (iMin + iMax) / 2;
int j = halfLen - i;
if (i < iMax && B[j-1] > A[i]){
iMin = iMin + 1; // i is too small
}
else if (i > iMin && A[i-1] > B[j]) {
iMax = iMax - 1; // i is too big
}
else { // i is perfect
int maxLeft = 0;
if (i == 0) { maxLeft = B[j-1]; }
else if (j == 0) { maxLeft = A[i-1]; }
else { maxLeft = Math.max(A[i-1], B[j-1]); }
if ( (m + n) % 2 == 1 ) { return maxLeft; }
int minRight = 0;
if (i == m) { minRight = B[j]; }
else if (j == n) { minRight = A[i]; }
else { minRight = Math.min(B[j], A[i]); }
return (maxLeft + minRight) / 2.0;
}
}
return 0.0;
}
}python代码
def median(A, B):
m, n = len(A), len(B)
if m > n:
A, B, m, n = B, A, n, m
if n == 0:
raise ValueError
imin, imax, half_len = 0, m, (m + n + 1) / 2
while imin <= imax:
i = (imin + imax) / 2
j = half_len - i
if i < m and B[j-1] > A[i]:
# i is too small, must increase it
imin = i + 1
elif i > 0 and A[i-1] > B[j]:
# i is too big, must decrease it
imax = i - 1
else:
# i is perfect
if i == 0: max_of_left = B[j-1]
elif j == 0: max_of_left = A[i-1]
else: max_of_left = max(A[i-1], B[j-1])
if (m + n) % 2 == 1:
return max_of_left
if i == m: min_of_right = B[j]
elif j == n: min_of_right = A[i]
else: min_of_right = min(A[i], B[j])
return (max_of_left + min_of_right) / 2.0class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m=nums1.size();
int n=nums2.size();
if(m>n)
{
vector<int> nums3;
nums3=nums2;
nums2=nums1;
nums1=nums3;
int temp=m;
m=n;
n=temp;
}
int imin=0;
int imax=m;
int half=(m+n+1)/2;
while(imin<=imax)
{
int i=(imin+imax)/2;
int j=half-i;
if( i<imax && nums2[j-1]>nums1[i] )
{
imin=imin+1;
}
else if( i>imin && nums1[i-1]>nums2[j] )
{
imax=imax-1;
}
else
{
int maxleft=0;
if(i==0)
{
maxleft=nums2[j-1];
}
else if(j==0)
{
maxleft=nums1[i-1];
}
else
{
if(nums1[i-1]>nums2[j-1])
maxleft=nums1[i-1];
else
maxleft=nums2[j-1];
}
if((m+n)%2==1)
{
return maxleft;
}
int minright=0;
if(i==m)
{
minright=nums2[j];
}
else if(j==n)
{
minright=nums1[i];
}
else
{
if(nums1[i]<nums2[j])
{
minright=nums1[i];
}
else
{
minright=nums2[j];
}
}
return (minright+maxleft)/2.0;
}
}
return 0.0;
}
};








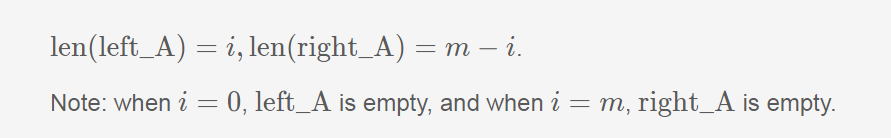


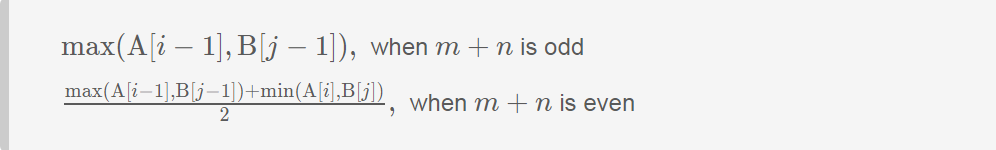
















 589
589

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










