Python：条件分支 if 语句全讲解

如果我拿出下面的代码，阁下该做何应对？

if not reset_excuted and (terminated or truncated):
	...
else:
    ...

前言：

消化论文代码的时候看到这个东西直接大脑冻结，没想过会在这么基础的东西上犯难

运算符优先级

在 Python 中，布尔运算符的优先级从高到低的顺序如下：

1. 括号 ()：最高优先级，可以用于明确运算顺序。

2. not：次高优先级。

3. and：次低优先级。

4. or：最低优先级。

优先级解析示例

示例 1: 使用括号

a = True
b = False
c = True

result = (a and not b) or c

在这个例子中：

1. 括号 首先被计算：a and not b 中 not b 计算为 not False，结果为 True。然后，True and True 计算为 True。

2. 最后，整体表达式变为 True or c，结果是 True。

示例 2: 不使用括号

x = False
y = True
z = False

result = x or y and not z

在这个例子中：

1. 优先级 按照 not > and > or：not z 计算为 not False，结果是 True。

2. 然后表达式转为 x or y and True。

3. 接着 y and True 计算为 True。

4. 最终计算为 x or True，结果是 True。

复杂示例

p = True
q = False
r = False

result = not (p and q) or r

在这个示例中：

1. 括号 首先被计算：p and q 计算为 True and False，结果是 False。

2. 然后，not False 计算为 True。

3. 最终表达式变为 True or r，结果是 True。

---

复杂if语句判断

在表达式 if not a and b 中，not 只对 a 生效，不影响 b。

• not 的优先级高于 and，这意味着它会先处理 a 的值。

• 首先计算 not a，这将返回 a 的布尔值的相反值。

• 然后，使用 and 运算符将结果与 b 进行比较。

if not para_A and (para_B or para_C):
    print("进入上面的分支")
else:
    print("进入下面的分支")

回到开头的示例，细细的捋一捋，在这段代码中：

在这里，not只对para_A生效，而不对(para_B or para_C)生效

要推算在什么情况下进入上面的分支或下面的分支，可以分析条件的每个部分。

分析条件

1. not para_A：要求 para_A 为 False。

   这意味着要进入上面的分支，para_A 必须是 False。

2. (para_B or para_C)：要求 para_B 或 para_C 至少有一个为 True。

   这意味着只要 para_B 为 True 或 para_C 为 True，这个部分就成立。

进入上面的分支的条件

整体条件为 not para_A and (para_B or para_C)，因此要进入上面的分支，必须满足以下条件：

• 条件 1：para_A 是 False。

• 条件 2：para_B 是 True 或 para_C 是 True（至少有一个为 True）。

进入下面的分支的条件

为了进入下面的分支，条件需要不成立，即：

1. 条件 A：para_A 是 True。

   这时 not para_A 为 False，条件就不成立。

2. 条件 B：para_A 是 False，但 para_B 和 para_C 都是 False。

   这时 (para_B or para_C) 为 False，条件也不成立。

总结条件表

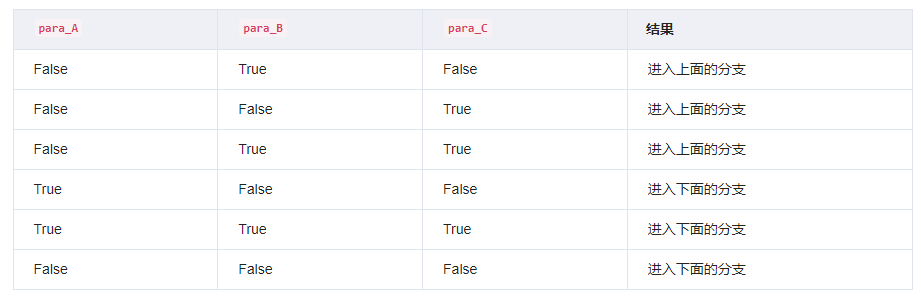
结论

• 进入上面的分支：当 para_A 为 False，且 para_B 或 para_C 至少有一个为 True。

• 进入下面的分支：当 para_A 为 True 或者 para_A 为 False，但 para_B 和 para_C 都为 False。

---

多分支语句elif

都写那么多了，干脆再补点东西显得更完整吧

在 Python 中，elif 是 “else if” 的缩写，用于在 if 语句中进行多重条件判断。它允许你在第一个 if 条件为 False 的情况下继续检查其他条件，从而实现更多的分支逻辑。

if condition1:
    # 当 condition1 为 True 时执行的代码
elif condition2:
    # 当 condition1 为 False 且 condition2 为 True 时执行的代码
elif condition3:
    # 当 condition1 和 condition2 都为 False 且 condition3 为 True 时执行的代码
else:
    # 当上面的所有条件都为 False 时执行的代码

德摩根定律

在j实际代码应用中，你基本用不上这个定律，上面的东西已经可以解决绝大部分问题了。但如果程序非要在if条件语句上向你发难，至少你也知道怎么应对

德摩根定律是布尔代数中的两个重要定律，它们提供了关于逻辑运算（与、或和非）之间关系的重要公式。这两个定律如下：

第一条定律：

not(A or B)≡notA and notB

解释：否定 A 或 B 相当于 A 和 B 的否定相与。

第二条定律：

not(A and B)≡notA or notB

解释：否定 A 且 B 相当于 A 的否定或 B 的否定。

举例说明

我们可以通过几个示例来理解这些定律：

示例 1：第一条定律

考虑 A = True 和 B = False：

• 计算 not(A or B)：A or B 是 Truenot(A or B) 是 False

• 计算 not A and not B：not A 是 Falsenot B 是 Truenot A and not B 是 False

结果是一致的：not(A or B) = False 和 not A and not B = False。

示例 2：第二条定律

考虑 A = True 和 B = False：

• 计算 not(A and B)：A and B 是 Falsenot(A and B) 是 True

• 计算 not A or not B：not A 是 Falsenot B 是 Truenot A or not B 是 True

同样，结果是相等的：not(A and B) = True 和 not A or not B = True。

文章转载自：El Psy Kongroo!

原文链接：https://www.cnblogs.com/hassle/p/18456599

体验地址：引迈 - JNPF快速开发平台_低代码开发平台_零代码开发平台_流程设计器_表单引擎_工作流引擎_软件架构