谈谈SVD和LSA
首先SVD和LSA是什么呢,SVD全称是singular value decomposition,就是俗称的奇异值分解,SVD的用处有很多,比如可以做PCA(主成分分析),做图形压缩,做LSA,那LSA是什么呢,LSA全称Latent semantic analysis,中文的意思是隐含语义分析,LSA算是topic model的一种,对于LSA的直观认识就是文章里有词语,而词语是由不同的主题生成的,比如一篇文章包含词语计算机,另一篇文章包含词语电脑,在一般的向量空间来看,这两篇文章不相关,但是在LSA看来,这两个词属于同一个主题,所以两篇文章也是相关的。
特征值特征向量
要谈到SVD,特征值和特征向量是需要首先交代的。具体内容可以在wiki上看,这里我做个简单的介绍。对于方阵M如果有
M∗v=λ∗v
v是个向量,λ是个数,那么我们称v是M的特征向量,λ是M的特征值,并且我们可以对M进行特征分解得到
M=Q∗Λ∗Q−1
其中Q是特征向量组成的矩阵,Λ是对角阵,对角线上的元素就是特征值。对于特征的几何理解就是矩阵M其实是一种线性变换,而线性变换对于向量的影响有两种,旋转和拉伸,而特征向量就是在这种线性变换下方向保持不变的向量,但是长度还是会作相应的拉伸,特征值就是拉伸的程度。
从另一个角度说如果我们取特征值比较大的几项,那么就是对原矩阵做了一种近似。
M≈Q1..k∗Λ1..k∗Q−11..k
这样我们就可以用更少的元素去近似的表示原矩阵,但是特征分解的限制比较多,比如要求矩阵必须是方阵
奇异值分解
wiki是个好东西,你要想深入了解的话,建议还是去看wiki。奇异值分解是将矩阵变成了这样的形式
M=U∗Σ∗VT
其中Σ依旧是对角阵,而U和V是正交矩阵正交矩阵是说U∗UT=I。
我们还是先回到矩阵是线性变换这个思路上。

如果我们用M去作用空间里的一组基,那么我们就会得到另一组基,如上图那样。那么我们旋转一下最初的一组基。

这样我们经过M的变换由一组正交基变换到了另一组正交基上面。也是也就是下面这样。
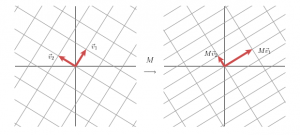
也就是我们有
M∗v1=σ1∗u1
M∗v2=σ2∗u2
并且对于任意一个向量x,我们有
x=v1∗(vT1∗x)+v2∗(vT2∗x)
于是我们可以得到
M∗x=M∗v1∗(vT1∗x)+M∗v2∗(vT2∗x)
M∗x=σ1∗u1∗(vT1∗x)+σ2∗u2∗(vT2∗x)
M=σ1∗u1∗vT1+σ2∗u2∗vT2
M=U∗Σ∗VT
恩,我们得到了和特征值和特征向量相似的东西,SVD分解出来的就是在M的线性变换下,正交基变换仍是正交基,而奇异值就是拉伸的程度。其实SVD和特征值和特征向量的关系还是很大的。
M∗MT=U∗Σ∗VT∗V∗ΣT∗UT
M∗MT=U∗Σ2∗UT
也就是说SVD求出的是M∗MT和MT∗M的特征向量。同样的得到这SVD分解这种形式后我们就可以利用他来对原数据进行降维操作。

这里我们分别将RBG矩阵进行SVD,左上角的是原图,其他的依次是取最大的100个,50个,20个,10个,5个奇异值做的近似图像。
# -*- coding: utf-8 -*-
from scipy import linalg, dot
from PIL import Image
def main(num=5):
im = Image.open('ai.jpg')
pix = im.load()
ma = [[], [], []]
for x in xrange(im.size[0]):
for i in xrange(3):
ma[i].append([])
for y in xrange(im.size[1]):
for i in xrange(3):
ma[i][-1].append(pix[x, y][i])
for i in xrange(3):
u, s, v = linalg.svd(ma[i])
u = u[:, :num]
v = v[:num, :]
s = s[:num]
ma[i] = dot(dot(u, linalg.diagsvd(s, num, num)), v)
for x in xrange(im.size[0]):
for y in xrange(im.size[1]):
ret = []
for i in xrange(3):
tmp = int(ma[i][x][y])
if tmp < 0:
tmp = 0
if tmp > 255:
tmp = 255
ret.append(tmp)
pix[x, y] = tuple(ret)
im.show()
im.save('test.jpg')
if __name__ == '__main__':
main()如果对矩阵先进行归一化,再SVD就是PCA的形式了,这种形式可以用方差最大化或者误差最小化来求得,具体可以去看PCA相关的东西。所以和scturtle讨论了下直接SVD的意义,但是最后也没得出什么结论。。。
隐含语义分析
终于讲到最后的隐含语义分析了,首先我们构造文本和词语的矩阵,也就是对于矩阵来说每一个向量表示一篇文章,每个向量里就是单词的出现次数(更好的是每个是单词的tf/idf值,tf/idf不在赘述,具体可以看wiki)。那么SVD分解之后,我们就得到了降维的矩阵,就是下面这个样子
就是说原来我们有1000000篇文章,总共有500000个单词,我们保留最大的100个来做降维,于是现在我们可以这样理解,我们保留了100个主题,其中U是文章对应的主题分布,而V则是主题对应的词语的分布,这样,我们可以减少噪音,并且这样计算文章间的相关性也更加合理,并且可以把相关的单词聚合到一起。代码如下
# -*- coding: utf-8 -*-
import os
import re
import heapq
import codecs
from math import log
from scipy import linalg
import unigram_good_turing as seg
seg.init()
def tfidf(docs):
doclen = len(docs)+1.0
for doc in docs:
wordtotal = sum(doc.values())+0.0
for word in doc:
tf = doc[word]/wordtotal
idf = log(doclen/(sum([word in tmp for tmp in docs])+1))
doc[word] = tf*idf
return docs
def solve(data):
re_zh, re_other = re.compile(ur"([\u4E00-\u9FA5]+)"), re.compile(ur"[^a-zA-Z0-9+#\n]")
blocks = re_zh.split(data)
for item in blocks:
if re_zh.match(item):
for i in seg.solve(item):
yield i
else:
tmp = re_other.split(item)
for x in tmp:
if x != '':
pass
def show(dic, p):
p = heapq.nlargest(10, enumerate(p), key=lambda x:x[1])
print ' '.join(map(lambda x:dic[x[0]], p))
def main():
names = os.listdir('text')
dic = {}
cnt = 0
ma = []
for name in names:
data = codecs.open('text/'+name, 'r', 'utf-8').read()
doc = {}
for word in solve(data):
if not word in dic:
dic[word] = cnt
cnt += 1
tmp = dic[word]
if tmp not in doc:
doc[tmp] = 0
doc[tmp] += 1
ma.append(doc)
ma = tfidf(ma)
ret = []
for item in ma:
tmp = []
for i in xrange(cnt):
if i in item:
tmp.append(item[i])
else:
tmp.append(0)
ret.append(tmp)
u, s, v = linalg.svd(ret)
for i in xrange(10):
show(dict(zip(dic.values(), dic.keys())), list(v[i]))
if __name__ == '__main__':
main()






















 1177
1177











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








