Using Uninitialized Memory for Fun and Profit

Using Uninitialized Memory for Fun and Profit

Posted on Friday, March 14, 2008.

frameborder="0" hspace="0" marginheight="0" marginwidth="0" scrolling="no" tabindex="0" vspace="0" width="100%" id="I0_1415783645351" name="I0_1415783645351" src="https://apis.google.com/se/0/_/+1/fastbutton?usegapi=1&size=small&annotation=none&origin=http%3A%2F%2Fresearch.swtch.com&url=http%3A%2F%2Fresearch.swtch.com%2Fsparse&gsrc=3p&ic=1&jsh=m%3B%2F_%2Fscs%2Fapps-static%2F_%2Fjs%2Fk%3Doz.gapi.zh_CN.NQqKTU9QqCI.O%2Fm%3D__features__%2Fam%3DAQ%2Frt%3Dj%2Fd%3D1%2Ft%3Dzcms%2Frs%3DAGLTcCOuqfxzOHsdilNI_Tb-I3oXTXt9-g#_methods=onPlusOne%2C_ready%2C_close%2C_open%2C_resizeMe%2C_renderstart%2Concircled%2Cdrefresh%2Cerefresh&id=I0_1415783645351&parent=http%3A%2F%2Fresearch.swtch.com&pfname=&rpctoken=71741081" data-gapiattached="true" style="position: absolute; top: -10000px; width: 450px; margin: 0px; border-style: none;">

This is the story of a clever trick that's been around for at least 35 years, in which array values can be left uninitialized and then read during normal operations, yet the code behaves correctly no matter what garbage is sitting in the array. Like the best programming tricks, this one is the right tool for the job in certain situations. The sleaziness of uninitialized data access is offset by performance improvements: some important operations change from linear to constant time.

Alfred Aho, John Hopcroft, and Jeffrey Ullman's 1974 book The Design and Analysis of Computer Algorithms hints at the trick in an exercise (Chapter 2, exercise 2.12):

Develop a technique to initialize an entry of a matrix to zero the first time it is accessed, thereby eliminating the  O(|| V|| 2) time to initialize an adjacency matrix.

Jon Bentley's 1986 book Programming Pearls expands on the exercise (Column 1, exercise 8; exercise 9 in the Second Edition):

One problem with trading more space for less time is that initializing the space can itself take a great deal of time. Show how to circumvent this problem by designing a technique to initialize an entry of a vector to zero the first time it is accessed. Your scheme should use constant time for initialization and each vector access; you may use extra space proportional to the size of the vector. Because this method reduces initialization time by using even more space, it should be considered only when space is cheap, time is dear, and the vector is sparse.

Aho, Hopcroft, and Ullman's exercise talks about a matrix and Bentley's exercise talks about a vector, but for now let's consider just a simple set of integers.

One popular representation of a set of n integers ranging from 0 to m is a bit vector, with 1 bits at the positions corresponding to the integers in the set. Adding a new integer to the set, removing an integer from the set, and checking whether a particular integer is in the set are all very fast constant-time operations (just a few bit operations each). Unfortunately, two important operations are slow: iterating over all the elements in the set takes time O(m), as does clearing the set. If the common case is that m is much larger than n (that is, the set is only sparsely populated) and iterating or clearing the set happens frequently, then it could be better to use a representation that makes those operations more efficient. That's where the trick comes in.

Preston Briggs and Linda Torczon's 1993 paper, “An Efficient Representation for Sparse Sets,” describes the trick in detail. Their solution represents the sparse set using an integer array nameddense and an integer n that counts the number of elements in dense. The dense array is simply a packed list of the elements in the set, stored in order of insertion. If the set contains the elements 5, 1, and 4, then n = 3 and dense[0] = 5, dense[1] = 1, dense[2] = 4:

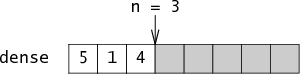
Together n and dense are enough information to reconstruct the set, but this representation is not very fast. To make it fast, Briggs and Torczon add a second array named sparse which maps integers to their indices in dense. Continuing the example, sparse[5] = 0, sparse[1] = 1, sparse[4] = 2. Essentially, the set is a pair of arrays that point at each other:

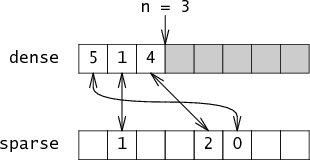
Adding a member to the set requires updating both of these arrays:

add-member(i):
    dense[n] = i
    sparse[i] = n
    n++

It's not as efficient as flipping a bit in a bit vector, but it's still very fast and constant time.

To check whether i is in the set, you verify that the two arrays point at each other for that element:

is-member(i):
    return sparse[i] < n && dense[sparse[i]] == i

If i is not in the set, then it doesn't matter what sparse[i] is set to: either sparse[i] will be bigger than n or it will point at a value in dense that doesn't point back at it. Either way, we're not fooled. For example, suppose sparse actually looks like:

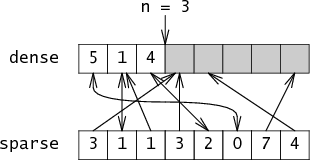
Is-member knows to ignore members of sparse that point past n or that point at cells in dense that don't point back, ignoring the grayed out entries:

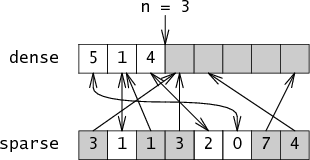
Notice what just happened: sparse can have any arbitrary values in the positions for integers not in the set, those values actually get used during membership tests, and yet the membership test behaves correctly! (This would drive valgrind nuts.)

Clearing the set can be done in constant time:

clear-set():
    n = 0

Zeroing n effectively clears dense (the code only ever accesses entries in dense with indices less than n), and sparse can be uninitialized, so there's no need to clear out the old values.

This sparse set representation has one more trick up its sleeve: the dense array allows an efficient implementation of set iteration.

iterate():
    for(i=0; i<n; i++)
        yield dense[i]

Let's compare the run times of a bit vector implementation against the sparse set:

Operation		Bit Vector		Sparse set
is-member		O(1)		O(1)
add-member		O(1)		O(1)
clear-set		O(m)		O(1)
iterate		O(m)		O(n)

The sparse set is as fast or faster than bit vectors for every operation. The only problem is the space cost: two words replace each bit. Still, there are times when the speed differences are enough to balance the added memory cost. Briggs and Torczon point out that liveness sets used during register allocation inside a compiler are usually small and are cleared very frequently, making sparse sets the representation of choice.

Another situation where sparse sets are the better choice is work queue-based graph traversal algorithms. Iteration over sparse sets visits elements in the order they were inserted (above, 5, 1, 4), so that new entries inserted during the iteration will be visited later in the same iteration. In contrast, iteration over bit vectors visits elements in integer order (1, 4, 5), so that new elements inserted during traversal might be missed, requiring repeated iterations.

Returning to the original exercises, it is trivial to change the set into a vector (or matrix) by making dense an array of index-value pairs instead of just indices. Alternately, one might add the value to thesparse array or to a new array. The relative space overhead isn't as bad if you would have been storing values anyway.

Briggs and Torczon's paper implements additional set operations and examines performance speedups from using sparse sets inside a real compiler.