学习笔记,仅供参考,有错必纠
聚类集成方法
7.1 引入
给定数据 D = { x 1 ⃗ , x 2 ⃗ , . . . , x m ⃗ } D=\{\vec{x_1},\vec{x_2},...,\vec{x_m}\} D={x1,x2,...,xm},其中第 i i i 个示例 x i ⃗ = ( x i 1 , x i 2 , . . . , x i d ) \vec{x_i}=(x_{i1},x_{i2},...,x_{id}) xi=(xi1,xi2,...,xid)是一个 d d d 维特征向量。聚类集成方法分为两步:
- 聚类生成:每个基聚类器 ξ ( q ) ( 1 ≤ q ≤ r ) \xi^{(q)}(1\leq q\leq r) ξ(q)(1≤q≤r) 将 D D D 分成 k ( q ) k^{(q)} k(q) 个簇 { C j ( q ) ∣ j = 1 , 2 , . . . , k ( q ) } \{C^{(q)}_j | j=1,2,...,k^{(q)}\} {Cj(q)∣j=1,2,...,k(q)}.换言之, ξ ( q ) \xi^{(q)} ξ(q) 返回的聚类结果可以被表示为一个标记向量 λ ( q ) \lambda^{(q)} λ(q),其中第 i i i 个元素 λ ( q ) i ∈ { 1 , 2 , . . . , k ( q ) } \lambda^{(q)_i}\in\{1,2,...,k^{(q)}\} λ(q)i∈{1,2,...,k(q)}表示了 x i ⃗ \vec{x_i} xi的聚类指派。
- 聚类结合:给定 r r r 个基聚类器 λ ( 1 ) , λ ( 2 ) , . . . λ ( r ) , \lambda^{(1)},\lambda^{(2)},...\lambda^{(r)}, λ(1),λ(2),...λ(r), 使用结合函数 τ ( ⋅ ) \tau(\cdot) τ(⋅) 将他们合并成最终包含 $ k$ 个簇的聚类结果 λ = τ ( { λ ( 1 ) , λ ( 2 ) , . . . λ ( r ) } ) \lambda =\tau(\{ \lambda^{(1)},\lambda^{(2)},...\lambda^{(r)} \}) λ=τ({λ(1),λ(2),...λ(r)}), 其中 λ i ∈ { 1 , 2 , 3 , . . . , k } \lambda_i\in\{ 1,2,3,...,k\} λi∈{1,2,3,...,k} 表示了 x i ⃗ \vec{x_i} xi 在最终的聚类中的簇类指派。例如我们已经生成了4个在7个示例上的基聚类结果:
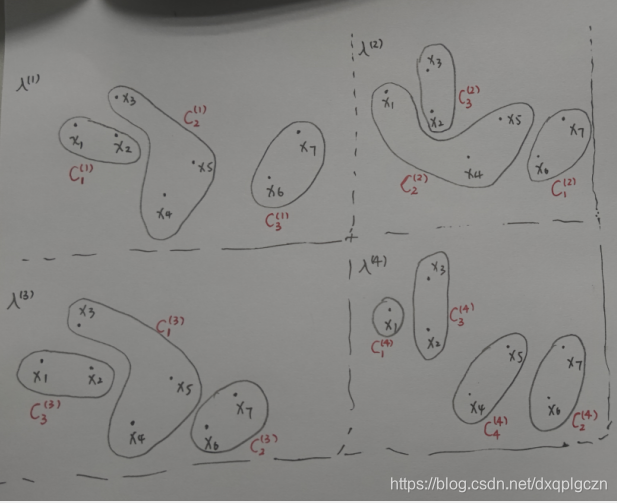
尽管 λ ( 1 ) \lambda^{(1)} λ(1) 和 λ ( 3 ) \lambda^{(3)} λ(3) 看起来不同,但实际上是等价的。右从图可以看出来:
聚类集成的研究重点在于聚类结合,成功获得聚类集成结果的关键是如何表达和聚合每个基聚类器的信息。近些年来的聚类集成方法,大致分为4种:
| 聚类集成方法 | 基聚类器的信息如何表达 | 如何结合多个聚类结果 |
|---|---|---|
| 基于相似度的方法 | 以相似度矩阵表达基聚类器的信息 | 使用矩阵平均的方式结合多个聚类结果 |
| 基于图的方法 | 以无向图表达基聚类器的信息 | 使用图分割的方式结合结果 |
| 基于重标记的方法 | 以标记向量表达基聚类器的信息 | 使用标记指派的方式结合结果 |
| 基于变换的方法 | 以特征重表示来表示基聚类器的信息 | 使用元聚类的方式结合结果 |
7.2 基于相似度的方法
7.2.1 基本思想
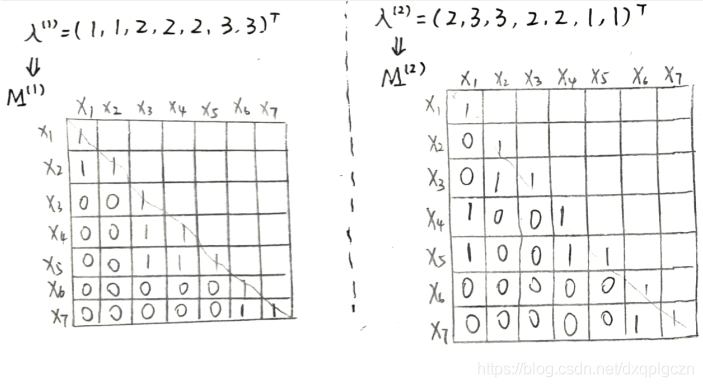
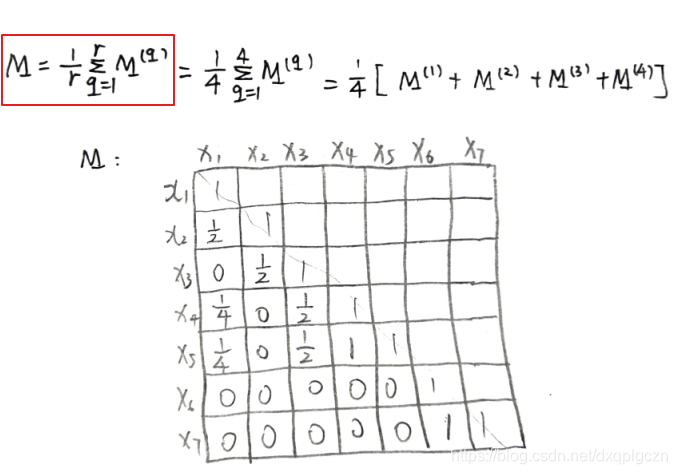
- 基于相似度的方法基本思想:是利用这些基聚类器形成一个 m × m m\times m m×m 一致相似度矩阵 M m × m M_{m\times m} Mm×m。然后基于相似度矩阵生成最终聚类结果。直观来讲,矩阵元素 M ( i , j ) M(i,j) M(i,j) 描述了示例 x i ⃗ \vec{x_i} xi 和 x j ⃗ \vec{x_j} xj 之间的相似度。首先,每个基聚类器 ξ ( q ) \xi^{(q)} ξ(q) 的聚类结果都可以获得一个 M m × m ( q ) M^{(q)}_{m\times m} Mm×m(q) 的相似性矩阵。然后对 r r r 个基聚类器进行平均得到一致相似度矩阵 M m × m M_{m\times m} Mm×m。

7.2.2 硬聚类
在硬聚类中, ξ ( q ) \xi^{(q)} ξ(q) 将数据集 D D D 分到 $k^{(q)} $ 个硬簇中,如K-means方法。每个示例仅属于一个簇。
M ( q ) ( i , j ) = { 1 , λ i ( q ) = λ j ( q ) 0 , λ i ( q ) ≠ λ j ( q ) M^{(q)}(i,j)=\begin{cases} 1,& \lambda^{(q)}_i=\lambda^{(q)}_j \\ 0,&\lambda^{(q)}_i\neq \lambda^{(q)}_j \end{cases} M(q)(i,j)={1,0,λi(q)=λj(q)λi(q)=λj(q)
M ( q ) M^{(q)} M(q) 对应一个二值矩阵,矩阵中的元素表示每对示例是否在同一个簇中出现。
- 例题
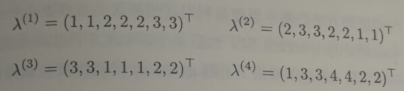 !
!
- 在得到一致相似度矩阵 M m × m M_{m\times m} Mm×m 后,可以有若干方式利用 M m × m M_{m\times m} Mm×m 获得聚类集成结果。如
- 将 1 − M ( i , j ) 1-M(i,j) 1−M(i,j) 视为 x i x_i xi 和 x j x_j xj 之间的距离,在数据集 D D D 上运行单链接、全链接或平均链接归并聚类方法;
- 以 M ( i , j ) M(i,j) M(i,j) 为权重的相似度图上应用分割聚类方法。
7.2.3 软聚类
在软聚类中, ξ ( q ) \xi^{(q)} ξ(q) 将数据集 D D D 分到 k ( q ) k^{(q)} k(q) 个软簇中。例如,基于GMM的聚类。示例 x i ⃗ \vec{x_i} xi 输入第 l l l 个簇的概率可写为 P ( l ∣ i ) P(l|i) P(l∣i) , 且 ∑ l = 1 k ( q ) P ( l ∣ i ) = 1 \sum^{k^{(q)}}_{l=1} P(l|i)=1 ∑l=1k(q)P(l∣i)=1 。基于相似度矩阵 M ( q ) M^{(q)} M(q) 可设置 M ( q ) ( i , j ) = ∑ l = 1 k ( q ) P ( l ∣ i ) ⋅ P ( l ∣ j ) M^{(q)}(i,j)=\sum^{k^{(q)}}_{l=1} P(l|i)\cdot P(l|j) M(q)(i,j)=∑l=1k(q)P(l∣i)⋅P(l∣j) 。换言之, M ( q ) M^{(q)} M(q) 对应的实值矩阵表示了每对示例在同一个簇出现的概率。
- 在得到一致相似度矩阵 M m × m M_{m\times m} Mm×m 后,可以有若干方式利用 M m × m M_{m\times m} Mm×m 获得聚类集成结果。如
- 将 1 − M ( i , j ) 1-M(i,j) 1−M(i,j) 视为 x i x_i xi 和 x j x_j xj 之间的距离,在数据集 D D D 上运行单链接、全链接或平均链接归并聚类方法;
- 以 M ( i , j ) M(i,j) M(i,j) 为权重的相似度图上应用分割聚类方法。
7.2.4 基于相似度方法的优缺点
-
优点:
基于相似度矩阵易于实现和聚合,基于相似度的方法具有概念简单的优点。此外一致相似度矩阵也为后续的分析提供了很好的基础,很多现有的在相似度矩阵上进行操作的聚类方法都可以用来生成最终的聚类集成。
-
缺点:
基于相似度矩阵的方法缺点在于其效率较低,计算和存储复杂度都是示例数目的平方级。因此,基于相似度的方法只能处理小规模或中等规模问题,处理大规模问题时会遇到困难。
7.3 基于图的方法
7.3.1 基本思想
-
基于图的聚类集成方法的基本想法是构造一个图 G = ( V , E ) G=(V,E) G=(V,E) 来整合基聚类器的聚类信息,然后通过图分解的方法生成最终的聚类集成结果。直观来讲,示例内在的分组信息都蕴含在图 G G G 中。
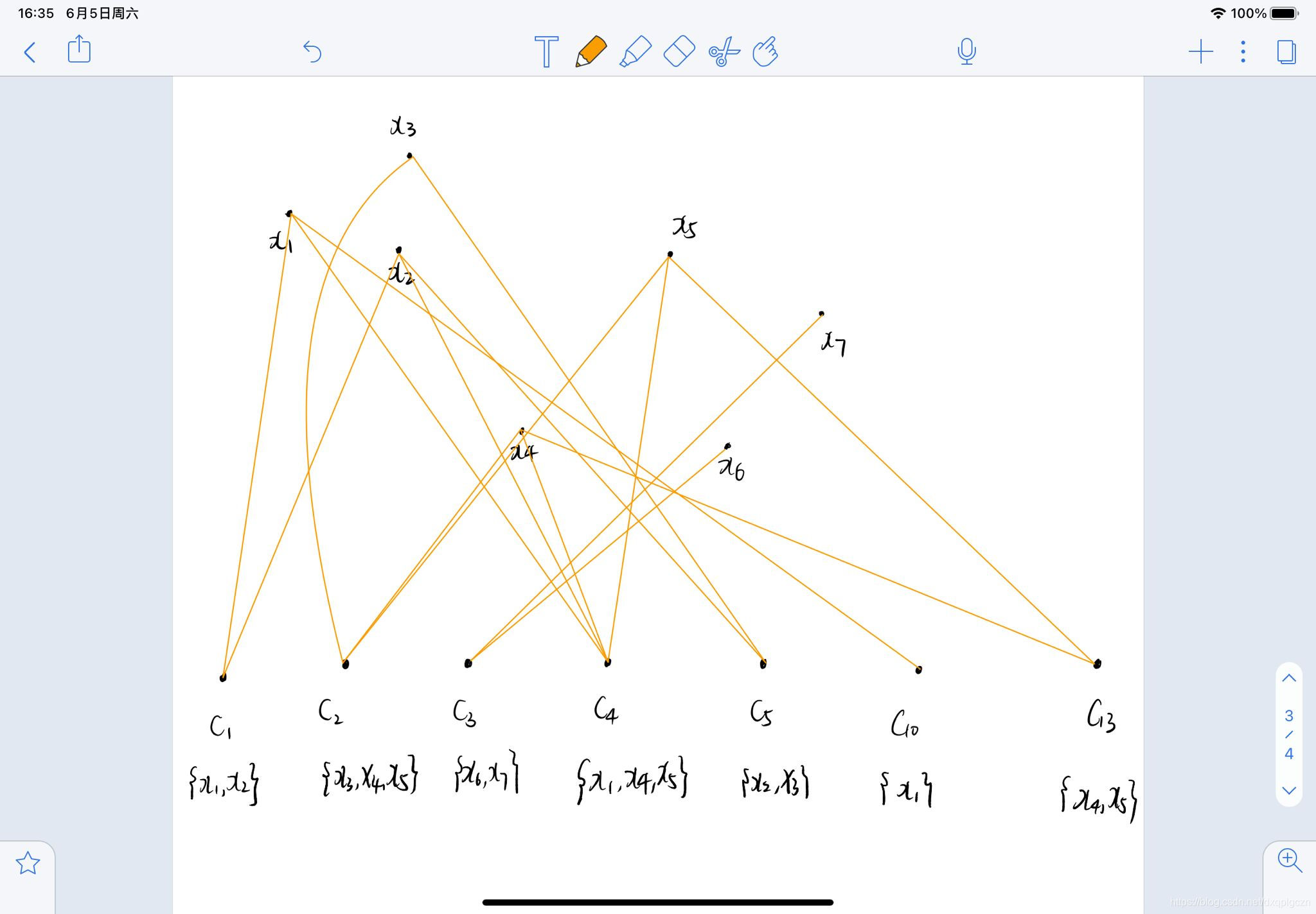
给定 r r r 个基聚类器 { λ ( q ) ∣ 1 ≤ q ≤ r } \{ \lambda^{(q)}| 1\leq q\leq r \} {λ(q)∣1≤q≤r} ,每个 λ ( q ) \lambda^{(q)} λ(q) 在数据集$ D$ 上生成 k ( q ) k^{(q)} k(q) 个簇,令 C = { C l ( q ) ∣ 1 ≤ q ≤ r , 1 ≤ l ≤ k ( q ) } C=\{C^{(q)}_l|1\leq q\leq r,1\leq l \leq k^{(q)}\} C={Cl(q)∣1≤q≤r,1≤l≤k(q)} ,表示包含了所有基聚类器中簇的集合,记 k ∗ = ∣ C ∣ = ∑ q = 1 r k ( q ) k^*=|C|=\sum^r_{q=1} k^{(q)} k∗=∣C∣=∑q=1rk(q) 为 C C C 的大小,即所有基聚类器包含的簇总数。不是一般性,为 C C C 中的簇重新标定序号 { C j ∣ 1 ≤ j ≤ k ∗ } \{ C_j|1\leq j\leq k^* \} {Cj∣1≤j≤k∗}。基于点集 V V V 的配置方式,有三种不同的方式来构建图 G = ( V , E ) G=(V,E) G=(V,E) 。
- V = D V=D V=D :HGPA算法(HyperGraph-Partitioning Algorithm)
- V = C V=C V=C:MCLA算法(Meta-CLustering Algorithm)
- V = D ∪ C V=D\cup C V=D∪C :HBGF算法(Hybrid Bipartite Graph Formulation)
7.3.2 HGPA算法
1. 构成超图
超图用于整合基聚类器的聚类信息
- V V V:样本点 x i ∈ D x_i\in D xi∈D 作为超图的顶点
- E E E:超边为基聚类器中属于同一个簇,就有一条超边。
- 权重:每条边的权重都为1
超图理解:https://blog.csdn.net/m0_37683327/article/details/91048782
例题
超图大概显示如彩色部分:
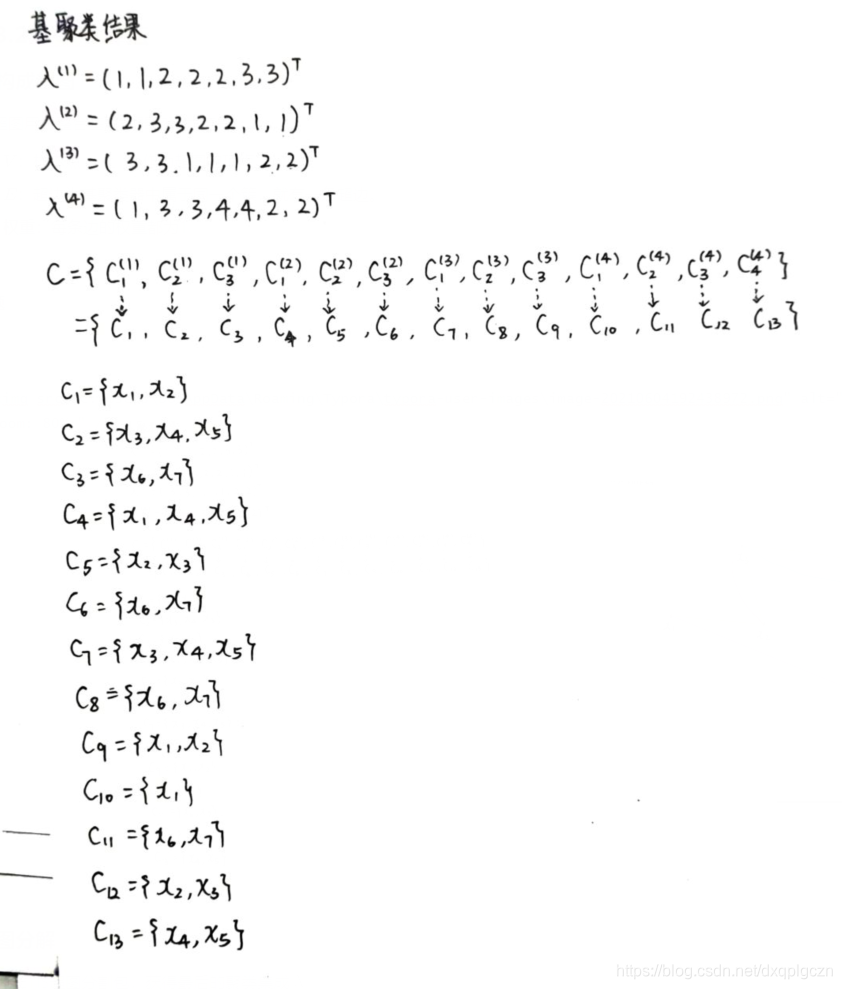
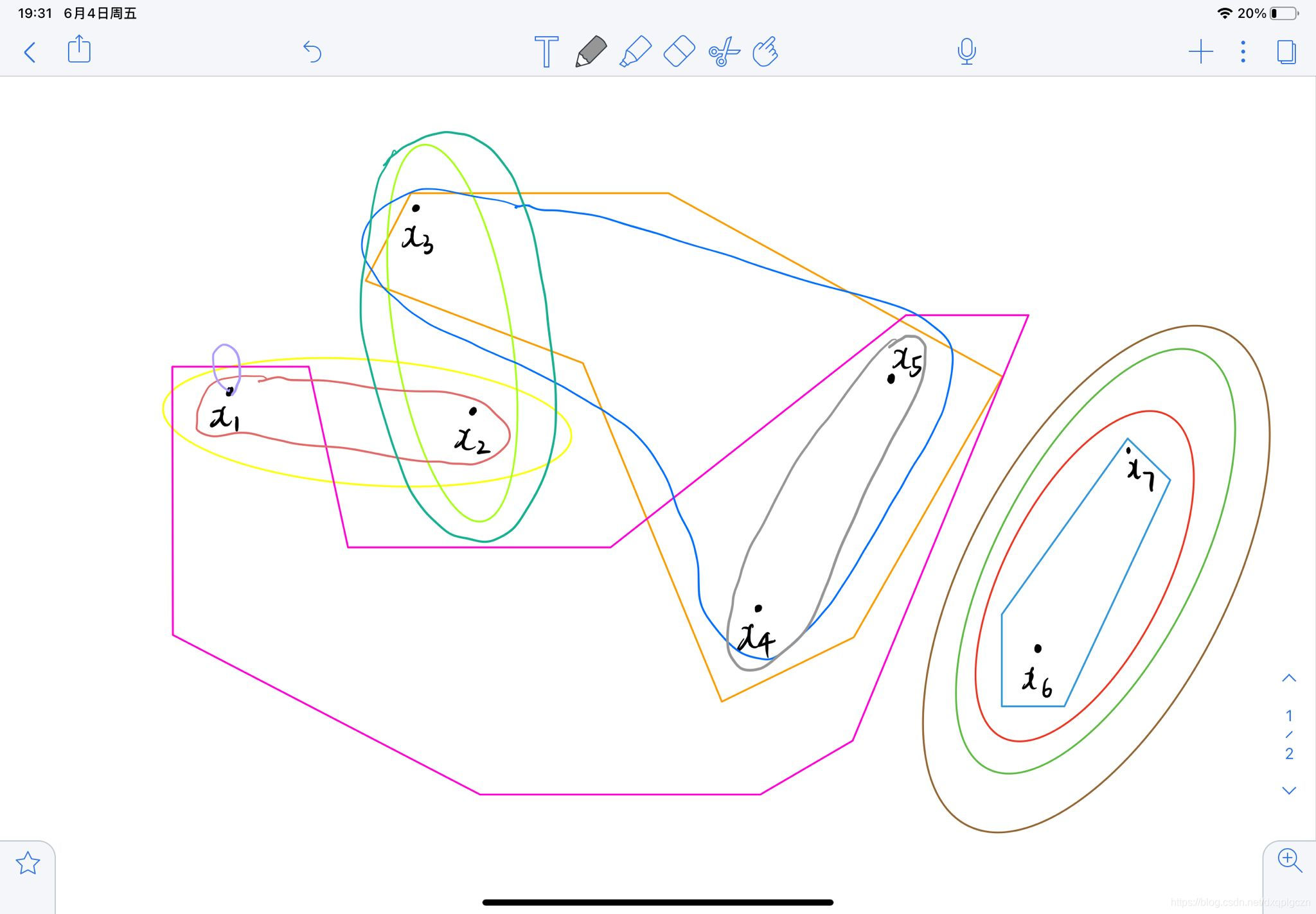
2. 图分解
HMETIS超图分割包,获得最后的聚类集成 λ \lambda λ
其中当且仅当在分割过程结束时、超边 C C C 中的点被两个或者两个以上分组囊括时,超边被视为一个切边。同时,还会在尽量满足分割所得的组的大小相差不大的前提下,最小化超图的切边。
HMETIS 后续碰到再补充
3. HGPA 算法伪代码

7.3.3 MCLA算法
1. 构成超图
- V V V:顶点集中的每个点对应一个簇 C i ∈ C C_i \in C Ci∈C
- E E E:超边为 任意两个簇之间都有边
- 权重:两个簇之间样本的重合率。 W i j = ∣ C i ∩ C j ∣ ∣ C i ∣ + ∣ C j ∣ − ∣ C i ∩ C j ∣ W_{ij}=\frac{|C_i \cap C_j|}{|C_i|+|C_j|-|C_i \cap C_j|} Wij=∣Ci∣+∣Cj∣−∣Ci∩Cj∣∣Ci∩Cj∣
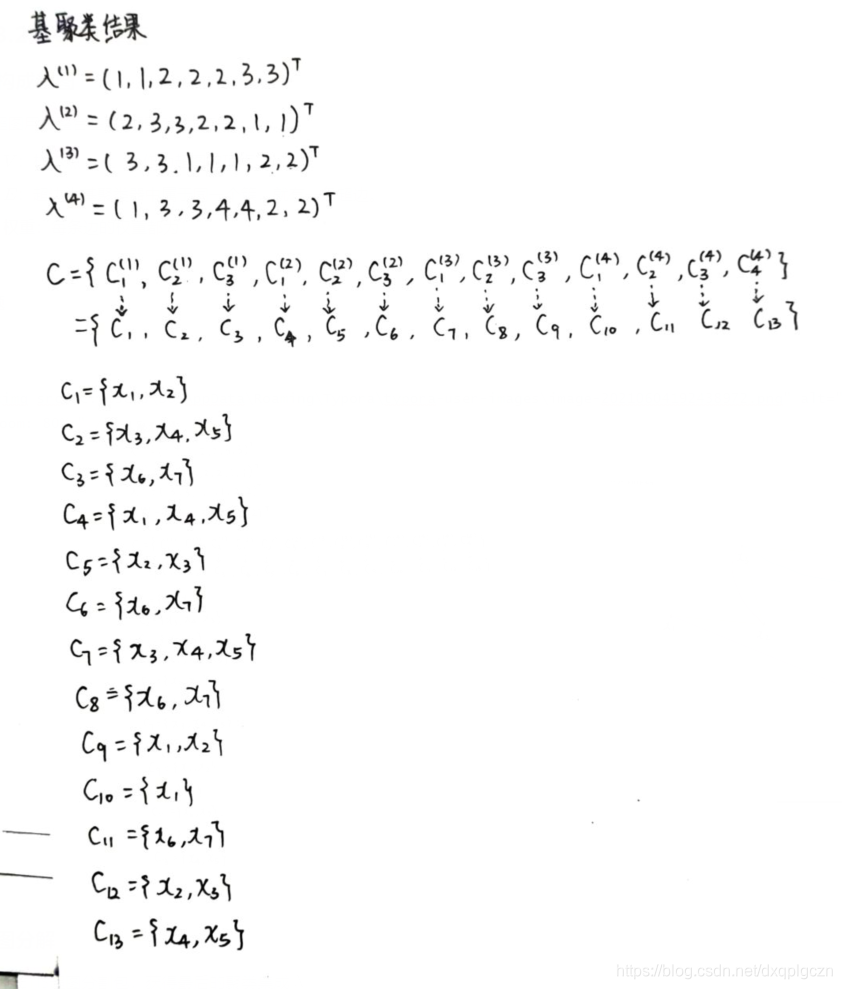
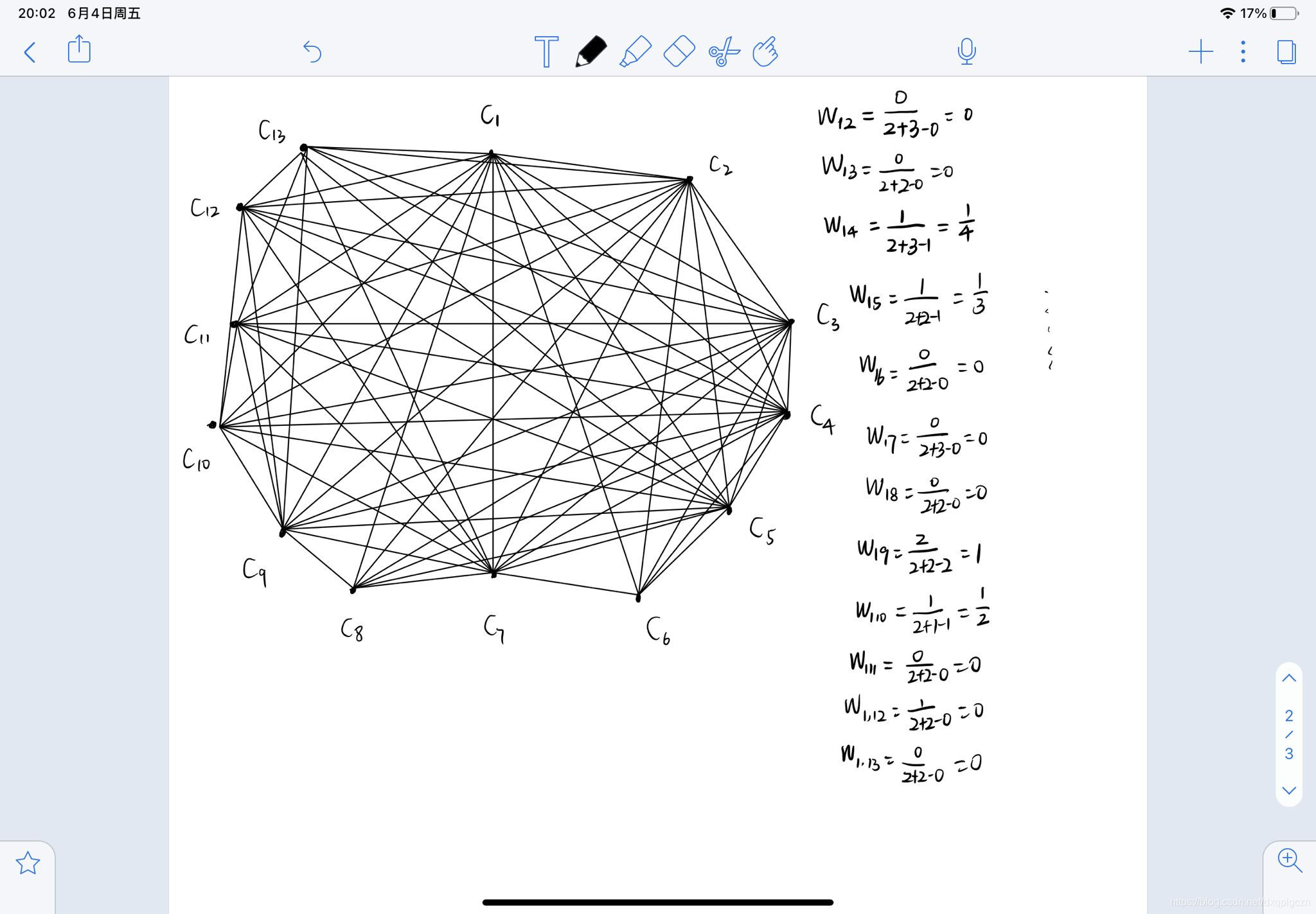
2. 图分解
用 METIS 将图 G G G 分割成 k k k 个平衡的元簇类 C p ( M ) ( p = 1 , 2 , . . . , k ) C^{(M)}_p(p=1,2,...,k) Cp(M)(p=1,2,...,k),每个元簇类被一个表征示例和元簇类间的关联程度的 m m m 维指示向量 h p ( M ) = ( h p 1 ( M ) , h p 2 ( M ) , . . . , h p m ( M ) ) h^{(M)}_p=(h^{(M)}_{p1},h^{(M)}_{p2},...,h^{(M)}_{pm}) hp(M)=(hp1(M),hp2(M),...,hpm(M)) 所表示。接下来,将每个示例分配给与其最相关的元簇类,就可以得到集成聚类簇 λ \lambda λ 。值得注意的是,此时不能保证每一个元簇类都至少获得一个示例,并且可采用随机分配簇类的方式来处理平局情况。
METIS 算法后续碰到在做解释。[Strehl & Ghosh,2002]
3. MCLA 算法伪代码

7.3.4 HBGF算法
1. 构成超图
- V:顶点对应了样本点和 C C C 中的簇
- E:如果 v i ∈ v j v_i\in v_j vi∈vj 则有边
- 权重:权重都为1
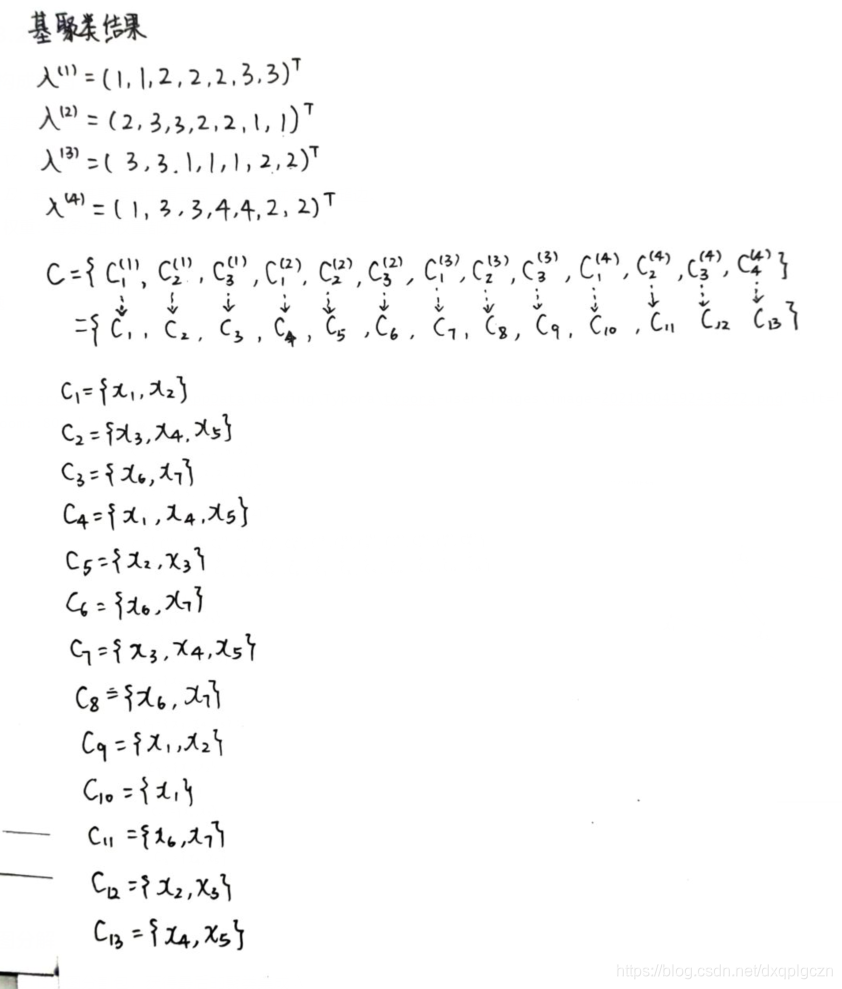
2. 图分解
在 G G G 上应用 SPEC 或者 HETIS 图分割包,可获得聚类集成 λ \lambda λ
3. HBGF 算法伪代码

7.3.5 基于图的方法的优缺点
-
优点:
- 计算复杂度和示例数目 m m m 呈线性关系。因此,这类方法为大规模数据集的聚类分析提供了一种可行的选择。
- 此外,基于图的方法能够处理更多超出成对关系的高阶示例间关系。
-
缺点:
- 基于图的缺点在于其性能很大程度上依赖用来生成最终聚类集成结果的图分割算法。由于图分割技术并不是专门为了聚类任务设计的,分割出的簇类也仅是图分割的副产品,因此可能削弱聚类集成的质量。
- 此外,大多数图分割算法,例如HMETIS,都有每个聚类应当包含大致相同数量的示例的约束,因此如果数据的内在簇结果是不平衡的,这些算法的聚类集成结果也将不准确。也就是说最后 k k k 个簇内样本数是一样的,因此基于图划分不能用于数据集群高度不平衡的情况。
7.4 基于重标记的方法
7.4.1 基本思想
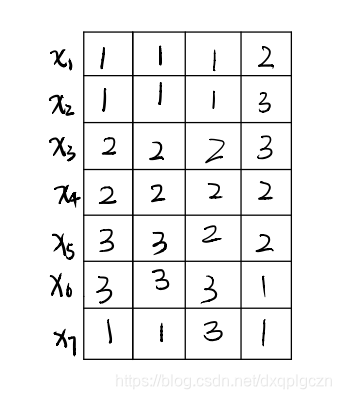
- 基于重标记的聚类集成方法的基本思想是校准或者重标记所有基聚类器的簇标记,使相同的标记指代基聚类器中相似的簇,然后在基于这些已校准的标记生成最终的聚类集成结果。与监督学习中的类标记代表特定类别不同,在非监督学习中,簇标记仅代表分组属性,且在不同类簇中不能直接比较比较。例如,给定两个聚类结果
λ
(
1
)
=
(
1
,
1
,
2
,
2
,
3
,
3
,
1
)
(
T
)
\lambda^{(1)}=(1,1,2,2,3,3,1)^{(T)}
λ(1)=(1,1,2,2,3,3,1)(T) 和
λ
(
2
)
=
(
2
,
2
,
3
,
3
,
1
,
1
,
2
)
(
T
)
\lambda^{(2)}=(2,2,3,3,1,1,2)^{(T)}
λ(2)=(2,2,3,3,1,1,2)(T) ,虽然每个示例的簇标记都不相同,但是他们实际上却是等价的。显然,应基于标记对应关系校正或重标记不同聚类结果下的簇标记。基于不同标记对应关系,重标记的方法可分为
- “硬标记对应“:每个基聚类器会将数据集 D = { x 1 ⃗ , x 2 ⃗ , . . . , x m ⃗ } D=\{ \vec{x_1},\vec{x_2},...,\vec{x_m} \} D={x1,x2,...,xm} 分组成数量相同的簇,即 k ( q ) = k ( q = 1 , 2 , 3 , . . , r ) k^{(q)}=k(q=1,2,3,..,r) k(q)=k(q=1,2,3,..,r)。 换句话说就是每个基聚类分成相同数量的簇。
- ”软标记对应“:每个基聚类器会将数据集 D = { x 1 ⃗ , x 2 ⃗ , . . . , x m ⃗ } D=\{ \vec{x_1},\vec{x_2},...,\vec{x_m} \} D={x1,x2,...,xm} 分组成数量不一定相同的簇,即 k ( q ) ( q = 1 , 2 , 3 , . . , r ) k^{(q)}(q=1,2,3,..,r) k(q)(q=1,2,3,..,r)。 换句话说就是每个基聚类分成可能不相同数量的簇。
7.4.2 硬标记对应
根据最大共享样本数目簇重标记

-
例题
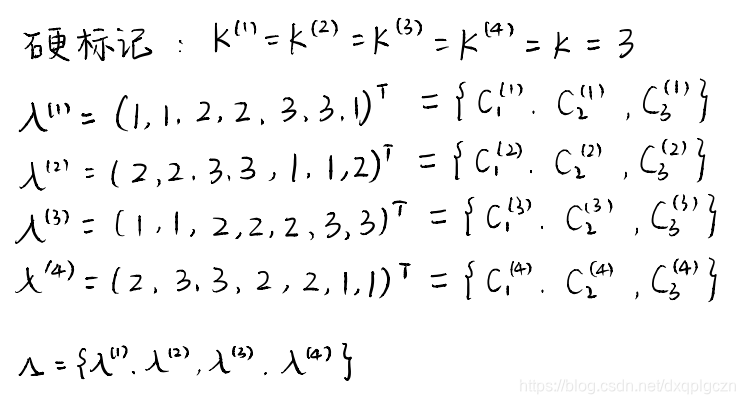



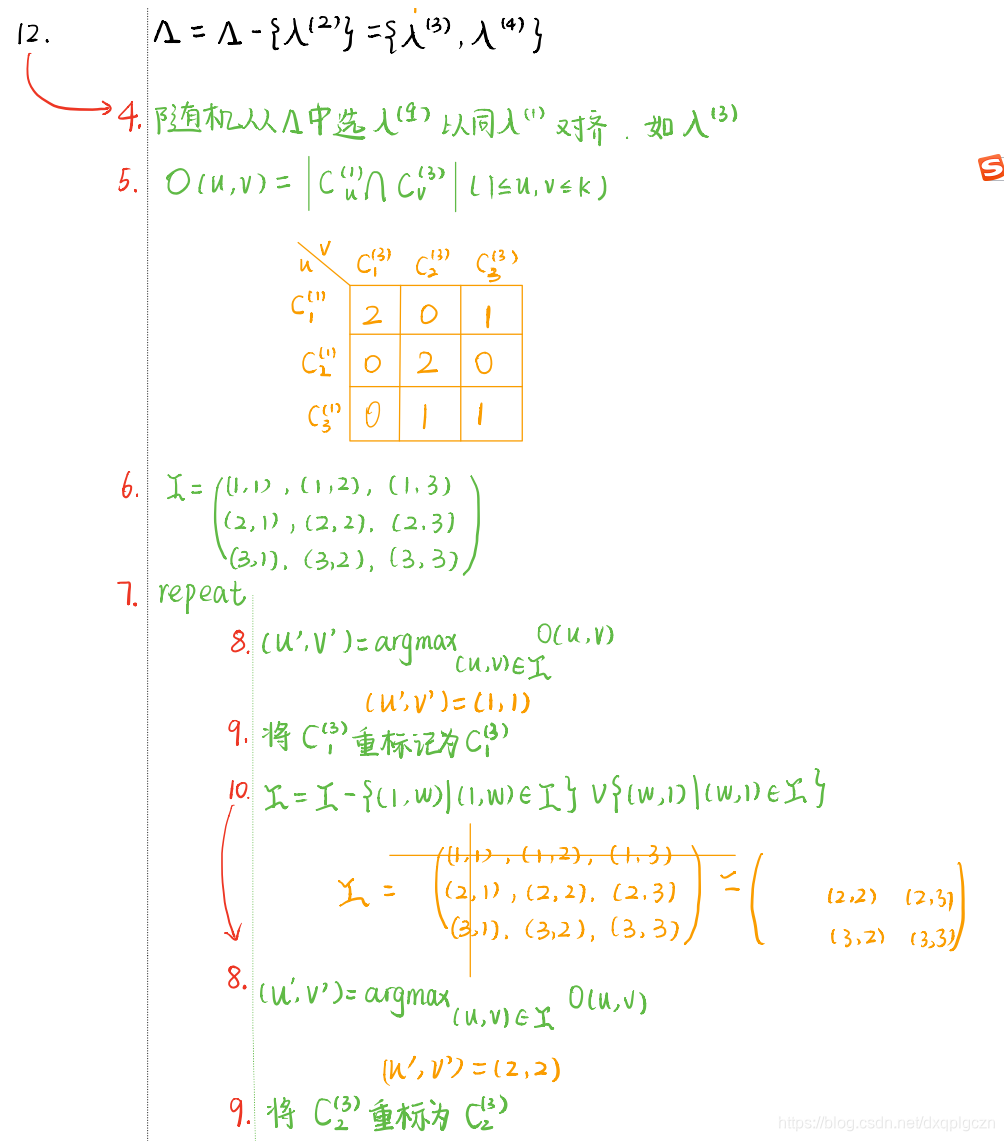

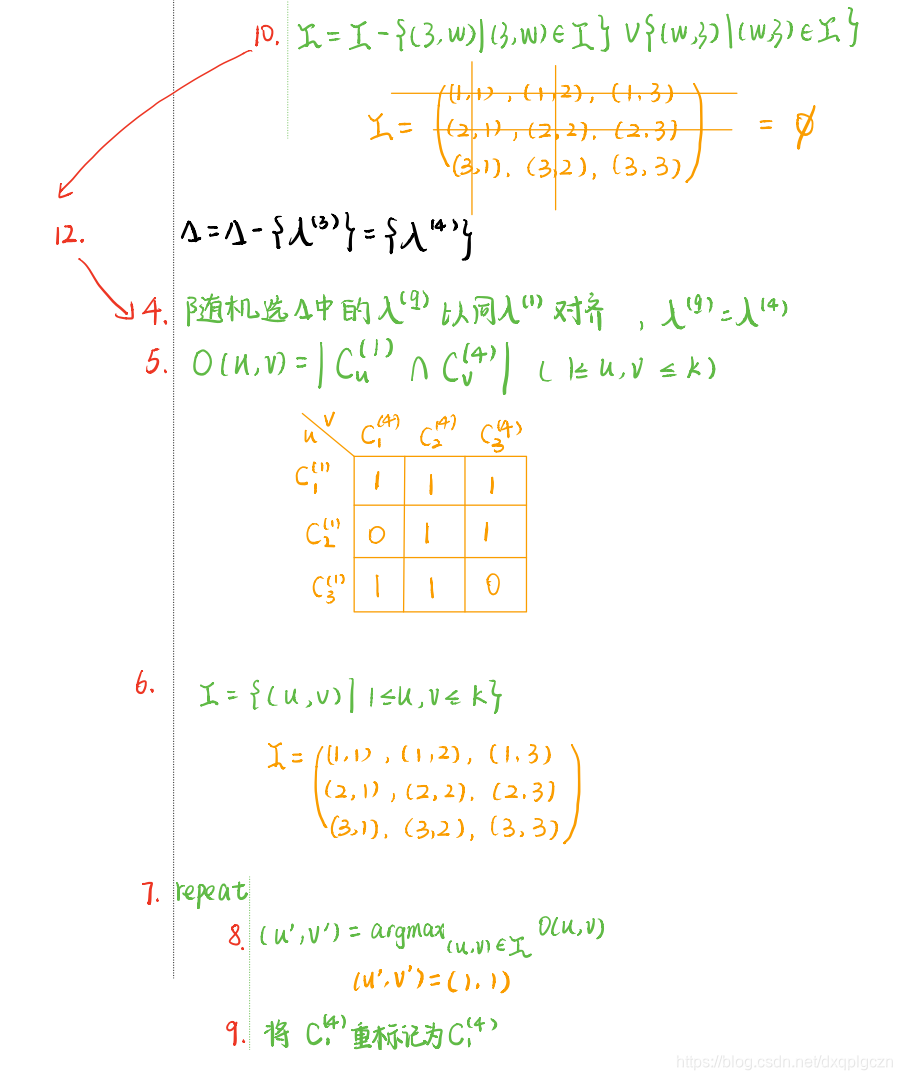
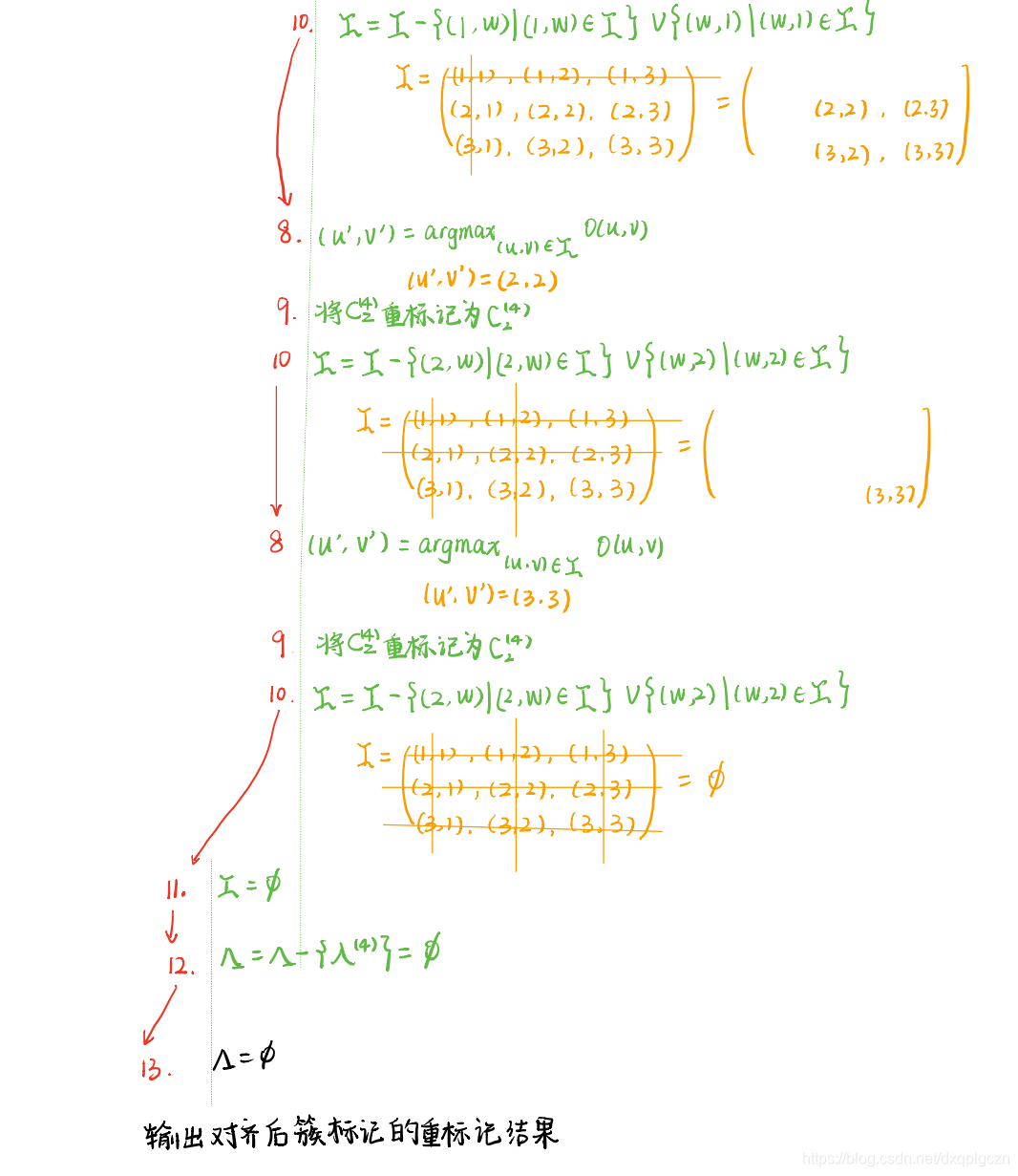

-
在不同基聚类被重标记之后,可以使用不同的结合策略获得最终的聚类集成结果 λ \lambda λ 。令 λ i ( q ) \lambda^{(q)}_i λi(q) 表示 x i ⃗ \vec{x_i} xi 在基聚类器 λ ( q ) \lambda^{(q)} λ(q) 对齐后的簇标记。以下是4种结合策略:
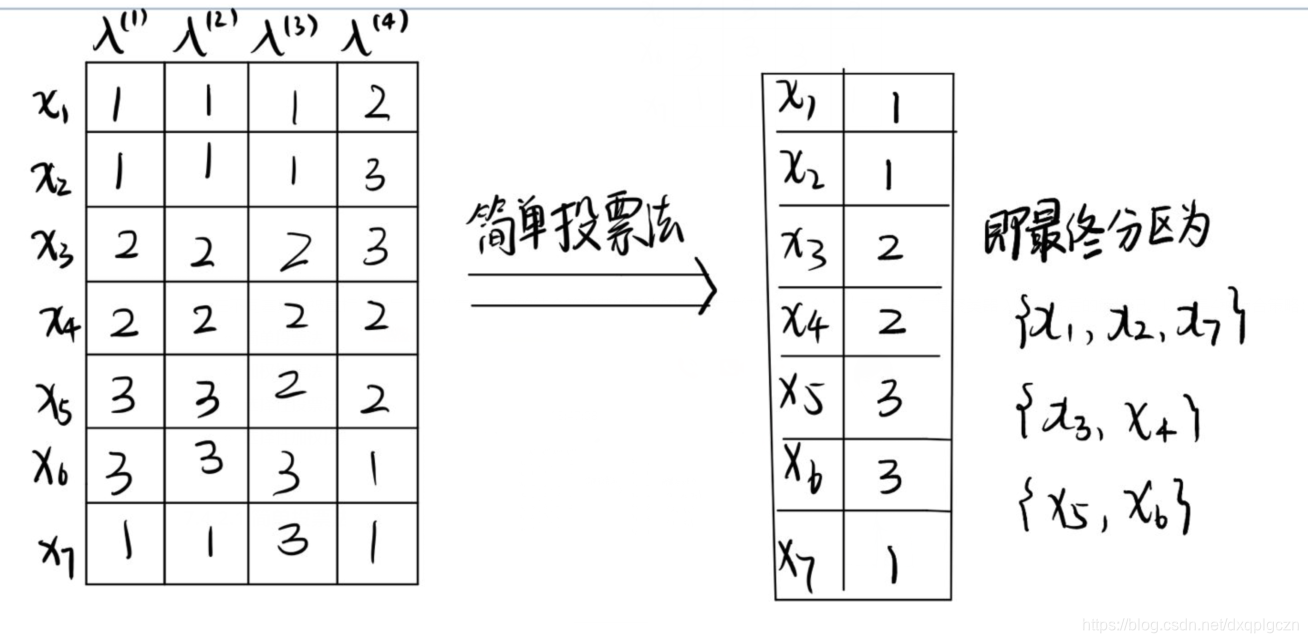
- 简单投票法
- 加权投票法
- 选择性投票法
- 选择性加权投票法
7.4.2.1 简单投票法
- 样本 x i ⃗ \vec{x_i} xi 的聚类集成标记 λ i \lambda_i λi 可有下式得到:
λ i = a r g m a x l ∈ { 1 , 2 , . . . , k } ∑ q = 1 r I ( λ i ( q ) = l ) \lambda_i=argmax_{l\in\{ 1,2,...,k \}} \sum^{r}_{q=1} I(\lambda^{(q)}_i=l) λi=argmaxl∈{1,2,...,k}q=1∑rI(λi(q)=l)
先求出每个样本用每个簇标记的个数,然后去最大的个数所代表的标记作为该样本的最终簇标记
7.4.2.2 加权投票法
-
加权投票法使用聚类结果间的互信息为每个 λ ( q ) \lambda^{(q)} λ(q) 生成权重。
步骤:
- 计算每两个基聚类器的联列表,和每个基聚类器中的每个簇的样本数;
- 计算每***两个***基聚类器之间的 N M I NMI NMI;
- 计算***每个***基聚类器的平均互信息;
- 计算每个基聚类器的权重;
- 就算每个样本的集成标记 λ i \lambda_i λi
1~2. 给定两个基聚类器 λ ( p ) \lambda^{(p)} λ(p) 和 λ ( q ) \lambda^{(q)} λ(q) ,令 m u = ∣ C u ( p ) ∣ m_u=|C^{(p)}_u| mu=∣Cu(p)∣, m v = ∣ C v ( q ) ∣ m_v=|C^{(q)}_v| mv=∣Cv(q)∣ , m u v = ∣ C u ( p ) ∩ C v ( q ) ∣ m_{uv}=|C^{(p)}_u \cap C^{(q)}_v| muv=∣Cu(p)∩Cv(q)∣; λ ( p ) \lambda^{(p)} λ(p) 和 λ ( q ) \lambda^{(q)} λ(q) 之间的归一化互信息 ϕ N M I \phi^{NMI} ϕNMI 可定义为:
ϕ N M I ( λ ( p ) , λ ( q ) ) = 2 m = ∑ u = 1 k ∑ v = 1 k m u v l o g k 2 ( m u v ⋅ m m u ⋅ m v ) \phi^{NMI}(\lambda^{(p)},\lambda^{(q)})=\frac{2}{m}=\sum^{k}_{u=1}\sum^{k}_{v=1}m_{uv}log_{k^2}(\frac{m_{uv}\cdot m}{m_u \cdot m_v}) ϕNMI(λ(p),λ(q))=m2=u=1∑kv=1∑kmuvlogk2(mu⋅mvmuv⋅m)- 如:
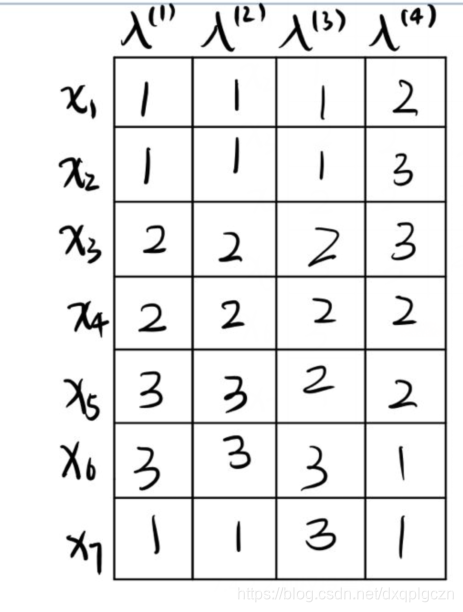
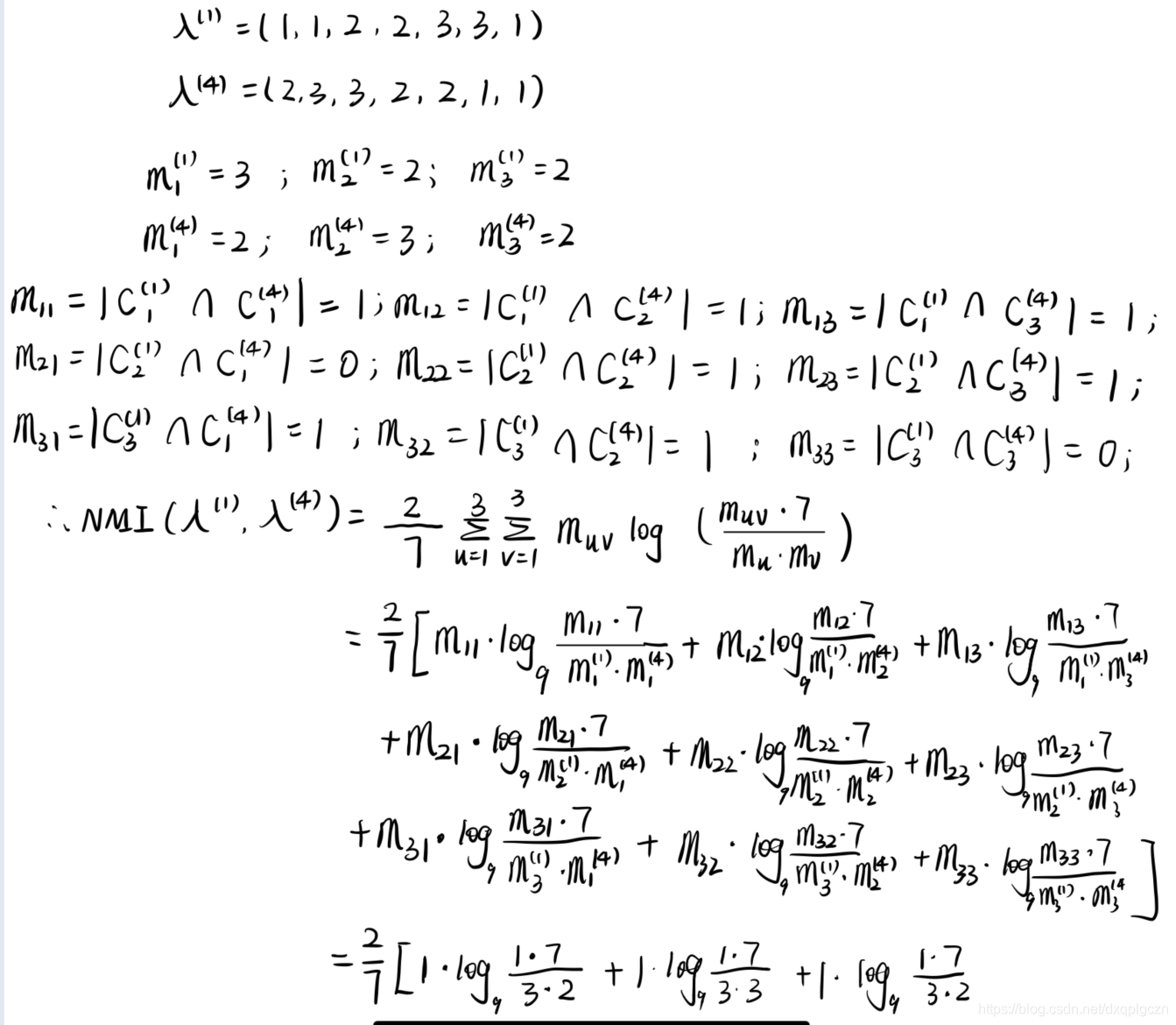
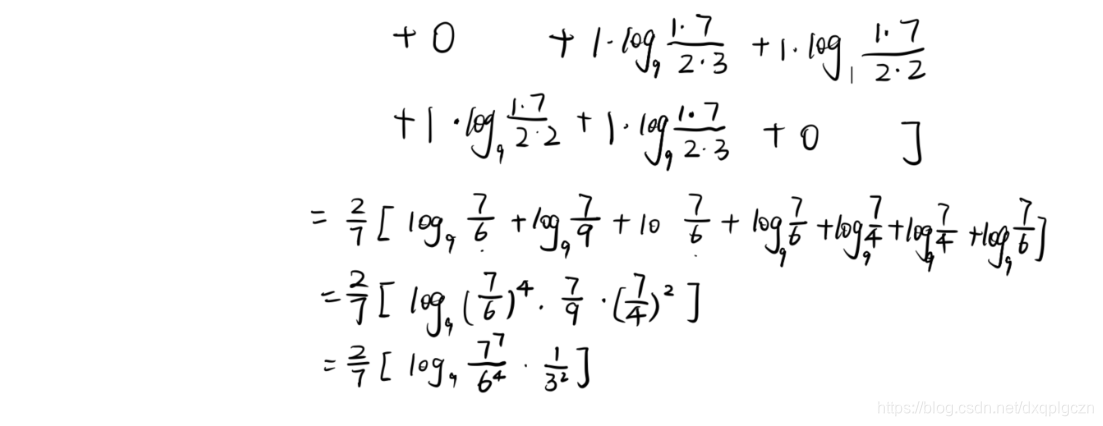
3. 对于每个基聚类器,可以计算得到平均互信息,即:
β
(
q
)
=
1
r
−
1
∑
p
=
1
,
p
≠
q
r
ϕ
N
M
I
(
λ
(
p
)
,
λ
(
q
)
)
\beta^{(q)}=\frac{1}{r-1}\sum^{r}_{p=1,p\neq q} \phi^{NMI}(\lambda^{(p)},\lambda^{(q)})
β(q)=r−11p=1,p=q∑rϕNMI(λ(p),λ(q))
直观来讲, ϕ ( q ) \phi^{(q)} ϕ(q) 越大,包含在 λ ( q ) \lambda^{(q)} λ(q) 中而不在其他基聚类器中的统计信息越少。
4. 定义
λ
(
q
)
\lambda^{(q)}
λ(q) 的权重为:
w
(
q
)
=
1
Z
⋅
β
(
q
)
w^{(q)}=\frac{1}{Z\cdot \beta^{(q)}}
w(q)=Z⋅β(q)1
其中 Z Z Z 是归一化因子,以使得 ∑ q = 1 r w ( q ) = 1 \sum^{r}_{q=1} w^{(q)}=1 ∑q=1rw(q)=1
5. 最后
x
i
⃗
\vec{x_i}
xi 的聚类集成标记
λ
i
\lambda_i
λi 为:
λ
i
=
a
r
g
m
a
x
l
∈
{
1
,
2
,
.
.
.
,
k
}
∑
q
=
1
r
w
(
q
)
⋅
I
(
λ
i
(
q
)
=
l
)
\lambda_i=argmax_{l\in \{ 1,2,...,k \}} \sum^r_{q=1}w^{(q)}\cdot I(\lambda^{(q)}_i=l)
λi=argmaxl∈{1,2,...,k}q=1∑rw(q)⋅I(λi(q)=l)
互信息参考资料:
信息熵及其概念:https://blog.csdn.net/am290333566/article/details/81187124
聚类间的互信息:https://blog.csdn.net/tyh70537/article/details/77145843
聚类间的互信息是用来衡量对同一数据集不同划分间的相似程度,换句话说就是用来衡量两个不同基聚类器之间的相似程度
7.4.2.3 选择性投票法
- 这类方法使用了集成修剪的策略。互信息权重 { w ( q ) ∣ q = 1 , 2 , . . . , r } \{w^{(q)}|q=1,2,...,r\} {w(q)∣q=1,2,...,r} 被用来选择结合基聚类器,其中权重小于阈值 w t h r w_{thr} wthr 的基聚类器会被排除。直接令 w t h r = 1 r w_{thr}=\frac{1}{r} wthr=r1 。 Q = { q ∣ w ( q ) ≥ 1 r , 1 ≤ q ≤ r } Q=\{ q|w^{(q)}\geq \frac{1}{r},1\leq q\leq r \} Q={q∣w(q)≥r1,1≤q≤r}, x i ⃗ \vec{x_i} xi 的聚类集成标记 λ i \lambda_i λi 为
λ i = a r g m a x l ∈ { 1 , 2 , . . . , k } ∑ q ∈ Q I ( λ i ( q ) = l ) \lambda_i=argmax_{l\in \{ 1,2,...,k \}} \sum_{q\in Q}I(\lambda^{(q)}_i=l) λi=argmaxl∈{1,2,...,k}q∈Q∑I(λi(q)=l)
7.4.2.4 选择性加权投票法
- 这是选择性投票法的加权版本, x i ⃗ \vec{x_i} xi 的聚类集成标记 λ i \lambda_i λi 为:
λ i = a r g m a x l ∈ { 1 , 2 , . . . , k } ∑ q ∈ Q w ( q ) ⋅ I ( λ i ( q ) = l ) \lambda_i=argmax_{l\in \{ 1,2,...,k \}} \sum_{q\in Q}w^{(q)}\cdot I(\lambda^{(q)}_i=l) λi=argmaxl∈{1,2,...,k}q∈Q∑w(q)⋅I(λi(q)=l)
7.4.3 软标记对应
不是很清楚,后续遇到资料再做说明 【Long et al.,2005]




7.5 基于变换的方法
7.5.1 基本思想
将每个示例重新表示为一个 r r r 元组,其中 r r r 是基聚类器的数量,第 q q q 个元素表示第 q q q 个基聚类器对该示例的簇分配,最终可以通过在 r r r 元组上进行簇类分析得到聚类集成结果。
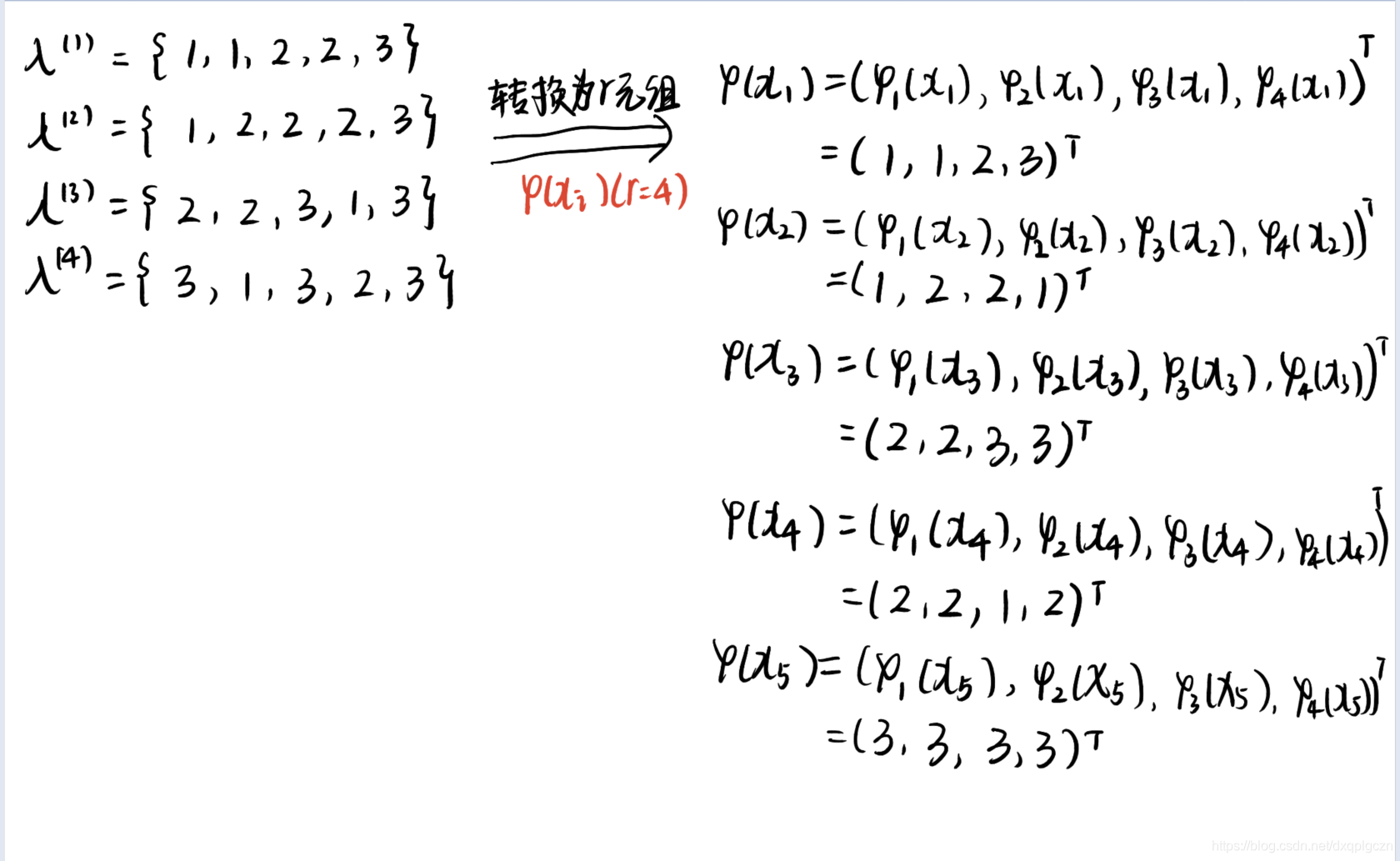
7.5.2 基于相似度的方法
- 将这些 r r r 元组定义一个相似度函数 s i m ( ⋅ , ⋅ ) sim(\cdot ,\cdot) sim(⋅,⋅)。即:
s i m ( φ ( x i ) , φ ( x j ) ) = ∑ q = 1 r I ( φ q ( x i ) = φ q ( x j ) ) sim(\varphi(x_i),\varphi(x_j))=\sum^{r}_{q=1} I(\varphi_q(x_i)=\varphi_q(x_j)) sim(φ(xi),φ(xj))=q=1∑rI(φq(xi)=φq(xj))
实际上就是样本之间的相似度为:两个样本被聚到相同簇的次数。越大表明越相似。以此来构建相似度矩阵;然后在使用传统的基于相似度矩阵的聚类算法获得最终集成结果。
7.5.3 基于概率框架的聚类技术
不是很懂













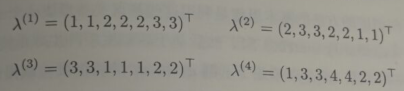













 889
889











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








