最小生成树算法总结

算法总结第5弹，最小生成树，有关生成树的问题有很多，这里先介绍个最常用的吧。

最小生成树

首先，生成树是建立在无向图中的，对于有向图，则没有生成树的概念，所以接下来讨论的图均默认为无向图。对于一个有n个点的图，最少需要n-1条边使得这n个点联通，由这n-1条边组成的子图则称为原图的生成树。一般来说，一个图的生成树并不是唯一的（除非原图本身就是一棵树）。

现在考虑带权图G，即图的边带权，则最小生成树就是在G中权值和最小的一颗生成树，显然最小生成树也不是唯一的，但是其权值唯一。有很多应用需要用到最小生成树的概念，比较直观的一个应用就是：有n个村庄，现在要在这些村庄之间修一些路，其中村庄i和村庄j之间的距离是Dij，现在要修最短的路使得所有村庄连接起来。

显然，这个问题可以直接套用最小生成树模型，找出最小生成树即找到了一个方案。

下面举一个最小生成树的例子：

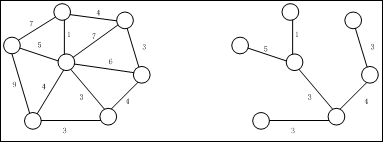
对于如何寻找一个带权图的最小生成树，已经有了专门的求解方法，在具体讲解这些算法之前，我们这里先来挖掘一下最小生成树的一些特性，即一颗生成树要成为最小生成树，需要满足什么条件。

MST性质：

设一个带权无向图G（V,E,W） （V代表点集，E代表边集，W代表权值集），且T为Ｇ的一颗生成树，对于Ｅ中任意一条不属于Ｔ的边ｅ，将其加入Ｔ中，会产生一条环（否则T不连通），如果e始终是环中权值最大的一条边，那么说明T满足MST性质。

以上是MST性质的定义，其中MST就是最小生成树的意思，但是现在并没有证明这个性质和最小生成树有什么关系，接下来将要证明，一颗生成树是最小生成树，当且仅当它满足MST性质。

引理1：对于图Ｇ（V,E,W）的两颗生成树T1和T2，若它们都满足MST性质，则它们的权值和相同。

证明：运用数学归纳法证明当有k条边在T1中而不在T2中时（0<=k<=n-1，同样的，这是也有k条边在T2中而不在T1中），T1的权值和等于T2的权值和。

1：首先，当k=0时，说明T1和T2的所有边都一样，则T1和T2是同一颗生成树，显然它们的权值和相等。

2：现在设当k<x时，T1和T2的权值和相等，现在要证明当k=x时，T1，T2权值和依然相等。考虑这样的边集S，它们在T1或T2中，但是不同时存在于T1和T2。在S中&#