快速幂:
//快速幂
#define ll long long
ll firstpow(ll x, ll pow) //位运算
{
ll result = 1;
while (pow)
{
if (pow & 1)
{
result *= x; result %= mod;
}
pow = pow >> 1;
x *= x; x %= mod;
}
return result;
}
不得不说,快速幂真的很爱出题。今天又做到了,get到几个新点。特此记录。
1、一个更简洁的代码
当然了,做法没有任何差别
ll power(ll a, int n)
{
ll res = 1;
for (; n; n /= 2, a *= a)
if (n&1)
res *= a;
return res;
}
2、补一下取余的公式
(a+b)%c=((a%c)+(b%c))%c 防止溢出
( a − b ) % c = ( ( a % c ) − b + c ) % c 加c, 防止出现负数
( a × b ) % c = ( ( a % c ) × ( b % c ) ) % c 防止溢出
3、关于分式的取余
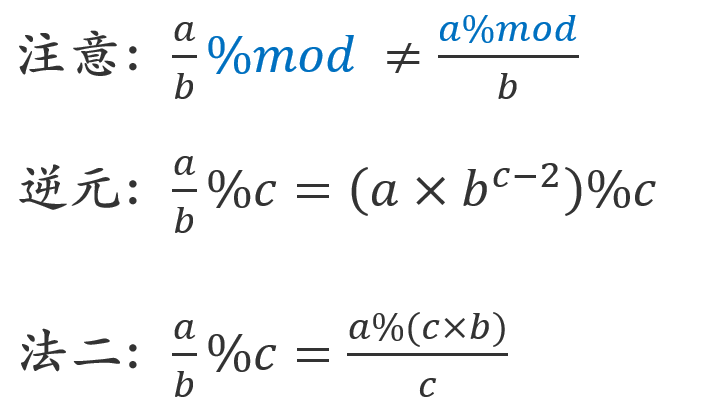
今天遇到的问题是:如果c并不是质数,那么就不好用上面两种方法(如:上帝造裸题的七分钟)。
4、矩阵快速幂 & 斐波那契数列
今天遇到的这题是:快速求解斐波那契数列的前n项。当然在时间空间足够的情况下,直接上数组就行。但是在比赛中,时间有限,而空间也仅支撑到106次方,对于动不动1018的测试点真的伤不起。
解法:矩阵快速幂。(所以在这里提是因为:明明之前都写过了,就下面例题里面那个,但是太久了,而且看快速幂的时候也懒得再看一遍例题,so,在这里强调一下)
点1:
//简而言之就是,斐波那契数列的 前n项和 = f(n+2)-1
//这一步,将求n项和,转化为求某一项
ans
= [f(1)+f(3)+f(5)+⋯+f(n)] + [f(2)+f(4)+f(6)+⋯+f(n−1)]
= [f(2)+f(3)+f(5)+⋯+f(n)] + [f(1)+f(2)+f(4)+f(6)+⋯+f(n−1)]−f(1)
= f(n+1)+f(n)−f(1)
= f(n+2)−1
点2:
//求斐波那契数列的第n项和,用矩阵快速幂的方法,可以大大节省时间。
//代码在下面例题,这里不重复。
矩阵快速幂:
- 定义
- 函数:矩阵乘法
- 函数:快速幂
- 主函数
定义:
//矩阵定义
struct node {
int mat[15][15];
}x, y;
矩阵乘法:
//矩阵乘法
node multi(node x, node y) {
node tmp;
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
tmp.mat[i][j] = 0;
for (int k = 0; k < len; k++) {
tmp.mat[i][j] += (x.mat[i][k] * y.mat[k][j]) % mod;
}
tmp.mat[i][j] = tmp.mat[i][j] % mod;
}
}
return tmp;
}
快速幂:
//矩阵快速幂
node matpow(node x, node y, int num) {
while (num) {
if (num & 1)
{
y = multi(y, x);
}
x = multi(x, x);
num = num >> 1;
}
return y;
}
例1:矩阵快速幂
| A为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),现要求Tr(A^k)%9973。 |
| Input 数据的第一行是一个T,表示有T组数据。 每组数据的第一行有n(2 <= n <= 10)和k(2 <= k < 10^9)两个数据。接下来有n行,每行有n个数据,每个数据的范围是[0,9],表示方阵A的内容。 |
| Output 对应每组数据,输出Tr(A^k)%9973。 |
Sample Input2 2 2 1 0 0 1 3 99999999 1 2 3 4 5 6 7 8 9 |
Sample Output2 2686 |
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
#define mod 9973
//矩阵定义,结构体
struct node
{
ll ma[11][11];
};
int n, k;
//矩阵乘法
node mul(node a, node b)
{
node ans;
memset(ans.ma, 0, sizeof(ans.ma));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
ans.ma[i][j] = (ans.ma[i][j] + a.ma[i][k] * b.ma[k][j]) % mod;
return ans;
}
//快速幂
node pow(node a, int pow)
{
//初始化ans矩阵为单位矩阵
node ans;
memset(ans.ma, 0, sizeof ans.ma);
for (int i = 1; i <= n; i++)
{
ans.ma[i][i] = 1;
}
//当pow的二进制位为1,ans就乘a。
//a每次都乘a
while (pow)
{
if (pow & 1)
{
ans = mul(ans, a);
}
a = mul(a, a);
pow >>= 1;
}
return ans;
}
int main()
{
int temp;
int t;
cin >> t;
while (t--)
{
scanf("%d %d", &n, &k);
node a;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
scanf("%d", &temp);
a.ma[i][j] = temp;
}
node ans = pow(a, k);
ll sum = 0;
for (int i = 1; i <= n; i++) sum = (sum + ans.ma[i][i]) % mod;
cout << sum << endl;
}
}
例2:矩阵快速幂+递推(斐波那契)
其实跟例1大同小异,放上来是因为斐波那契这种矩阵解法很不错,比递归快多了
In the Fibonacci integer sequence,F0= 0,F1= 1, andFn=Fn− 1+Fn− 2forn≥ 2. For example, the first ten terms of the Fibonacci sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … An alternative formula for the Fibonacci sequence is  Given an integern, your goal is to compute the last 4 digits ofFn. Given an integern, your goal is to compute the last 4 digits ofFn. |
Sample Input 0 9 999999999 1000000000 -1 |
Sample Output 0 34 626 6875 |
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 10000
#define ll long long
using namespace std;
//矩阵定义,结构体
struct mat
{
ll m[11][11];
mat()
{
memset(m, 0, sizeof(m));
}
};
ll n = 2, k;
//矩阵乘法
mat mul(mat a, mat b)
{
mat ans;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;
return ans;
}
//快速幂
mat pow(mat a, int pow)
{
//初始化ans矩阵为单位矩阵
mat ans;
for (int i = 1; i <= n; i++)
{
ans.m[i][i] = 1;
}
//当pow的二进制位为1,ans就乘a。
//a每次都乘a
while (pow)
{
if (pow & 1)
{
ans = mul(ans, a);
}
a = mul(a, a);
pow >>= 1;
}
return ans;
}
int main()
{
int x;
while (scanf("%d", &x) != EOF)
{
if (x == -1)break;
mat a;
a.m[1][1] = 1, a.m[1][2] = 1;
a.m[2][1] = 1, a.m[2][2] = 0;
a = pow(a, x);
if (x)
{
printf("%lld\n", a.m[1][2]);
}
else
{
printf("0\n");
}
}
}
例3:矩阵快速幂+递推
| Dwarfs种了一株非常有意思的植物,这株植物像一个方向向上的三角形。它有一个迷人的特点,那就是在一年后一株方向向上的三角形的植物就会被分成4株三角形的植物:它们当中的三株方向是向上的,一株方向是向下的。 又一年之后,每株植物都会分成四个,规则如上。之后的每年都会重复这一过程。下面的图说明了这一发展过程。 请帮助Dwarfs算出n年后将会有多少个方向向上的三角形。 |

第一行包括一个整数n(0<=n<=101810^{18}1018),即这植株生长的总年份。 ps:c++选手请不要用%lld来读取或输出long long类型,cin/cout或%I64d更好一些。
0 1 2 3Output
输出一个整数,即n年后向上的三角形的个数(答案对1000000007(10910^{9}109+7)取模)
1 3 10 36
解:
没给出递推式,但可以推出

#include <cstdio>
#include <iostream>
#define ll long long
#define n 2
#define mod 1000000007;
using namespace std;
struct mat
{
ll m[2][2];
mat()
{
memset(m, 0, sizeof(m));
}
};
mat multi(mat a, mat b)
{
int i, j, k;
mat result;
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
for (k = 0; k < n; k++)
{
result.m[i][j] += (a.m[i][k] * b.m[k][j]);
result.m[i][j] %= mod;
}
}
}
return result;
}
mat powfirst(mat a, int pow)
{
mat result;
result.m[0][0] = result.m[1][1] = 1;
while (pow)
{
if (pow & 1) result = multi(result, a);
a = multi(a, a);
pow = pow >> 1;
}
return result;
}
int main()
{
int x;
mat a;
mat result;
while (scanf("%d", &x) != EOF)
{
result.m[0][0] = result.m[1][0] = 1;
a.m[0][0] = 4;
a.m[0][1] = -1;
a.m[1][0] = 0;
a.m[1][1] = 2;
result = multi(powfirst(a, x), result);
cout << result.m[0][0] << endl;
}
}
例4:矩阵快速幂+递推
(sqrt(2)+sqrt(3))^2n %1024向下取整的值
总结
几个易错的点:
- 阶数n和mod记得在宏定义
- 矩阵a要在while里面初始化
- 一般是aaaab,不是baa*a。
刚开始想简化一下,就想这样写
powfirst函数
{
result初始化为b而非单位矩阵;//该result是矩阵连乘的第一个矩阵,与主函数中result不是同一个意思
……
}
主函数
{
定义result函数;
result = powfirst(a,pow);
输出result的某一位;
}
但是这样就baa*a了,所以应该是
powfirst函数
{
result初始化为单位矩阵;//该result是矩阵连乘的第一个矩阵,与主函数中result不是同一个意思
……
}
主函数
{
定义result并初始化为b;
a = powfirst(a,pow);
result = multi(a,result);
cout result的某一位;
}

参考:
例题:






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








