Large scale machine learning - Learning with large datasets

In next few classes, we'll talk about large scale machine learning. That is algorithms that dealing with big datasets.

Motivation

Figure-1

 

We've already seen that one of the best ways to get a high performance machine learning system is if you take a low-bias learning algorithm, and train that on a lot of data. One early example was classifying between confusable words as figure-1. For this example, so long as you feed the algorithms a lot of data, it seems to do very well. This has led to the saying that often it's not who has the best algorithm that wins, it's who has the most data.

Problems of learning with large datasets

Figure-2

Learning with large datasets comes with its own unique problems, specifically, computational problem. As shown in figure-2, it shows the gradient descent rule of linear regression. And it has 100 million examples. This is pretty realistic for many modern datasets. To perform a single step of gradient descent, you need to carry out a summation over 100 million terms. This is expensive. In the next classes, we'll talk about techniques for either replacing this algorithm with something else or to find more efficient ways to compute this derivative. By the end of the classes on large scale machine learning, you'll know how to fit models, linear regression, logistic regression, neural networks and so on, even the datasets have, say, 100 million examples.

High bias or high variance?

Before we put an effort into training a model with 100 million examples, we should ask ourselves, why not just use 1000 examples? Maybe we can randomly pick a subset of 1000 examples out of 100 million examples and train our algorithm on just 1000 examples. So before investing the effort into actually developing the software needed to train these massive models, it is often a good sanity check if training on just 1000 examples might do just as well.

Figure-3

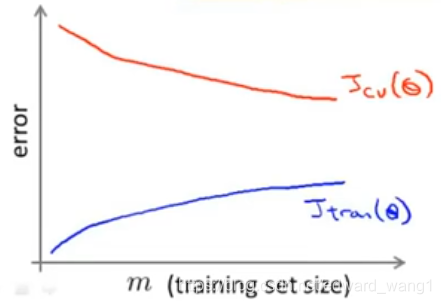
To sanity check that if using a much smaller training set like 1000 might do just as well, the usual method is of plotting the learning curves.

So if you were to plot the learning curves, and if your training objectives were to look like the blue line in figure-3. And if your cross validation set objective was look like the red line, then this looks like a high-variance learning algorithm (see http://edwardwangcq.com/advice-for-applying-machine-learning-learning-curves/), and we will be more confident that adding extra training examples would improve performance.

Figure-4

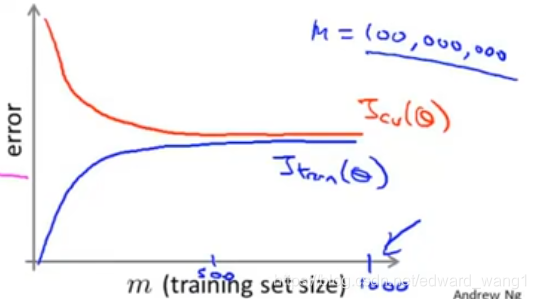
Whereas in contrast, if your learning curves were like that in figure-4. Then this looks like the classical high-bias learning algorithm. Then it seems unlikely that increasing m to 100 million will do much better. And you'd be just fine sticking to m=1000. When you were in such situation, one natural thing to do would be to add extra features or add extra hidden units to your neural network and so on, so that you end up with a situation closer to that of figure-3. This gives you more confidence by trying to add infrastructure to change the algorithm to use much more than a thousand examples. That might actually be a good use of your time.

Next, we'll come up with computationally reasonable ways to deal with very big datasets. We'll see two main ideas: Stochastic Gradient Descent & Map Reduce for dealing with very big datasets.

<end>