机器学习（二）：k近邻法（kNN）

更多内容关注公众号：数学的旋律

tb店铺搜：FUN STORE玩物社，专业买手挑选送礼好物

引言

    k近邻法（k-nearest neighbor, kNN）是一种基本分类与回归方法，其基本做法是：给定测试实例，基于某种距离度量找出训练集中与其最靠近的k个实例点，然后基于这k个最近邻的信息来进行预测。
    通常，在分类任务中可使用“投票法”，即选择这k个实例中出现最多的标记类别作为预测结果；在回归任务中可使用“平均法”，即将这k个实例的实值输出标记的平均值作为预测结果；还可基于距离远近进行加权平均或加权投票，距离越近的实例权重越大。
    k近邻法不具有显式的学习过程，事实上，它是懒惰学习（lazy learning）的著名代表，此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理。
    本文只讨论分类问题中的k近邻法。

一、k近邻法的三要素

    距离度量、k值的选择及分类决策规则是k近邻法的三个基本要素。根据选择的距离度量（如曼哈顿距离或欧氏距离），可计算测试实例与训练集中的每个实例点的距离，根据k值选择k个最近邻点，最后根据分类决策规则将测试实例分类。
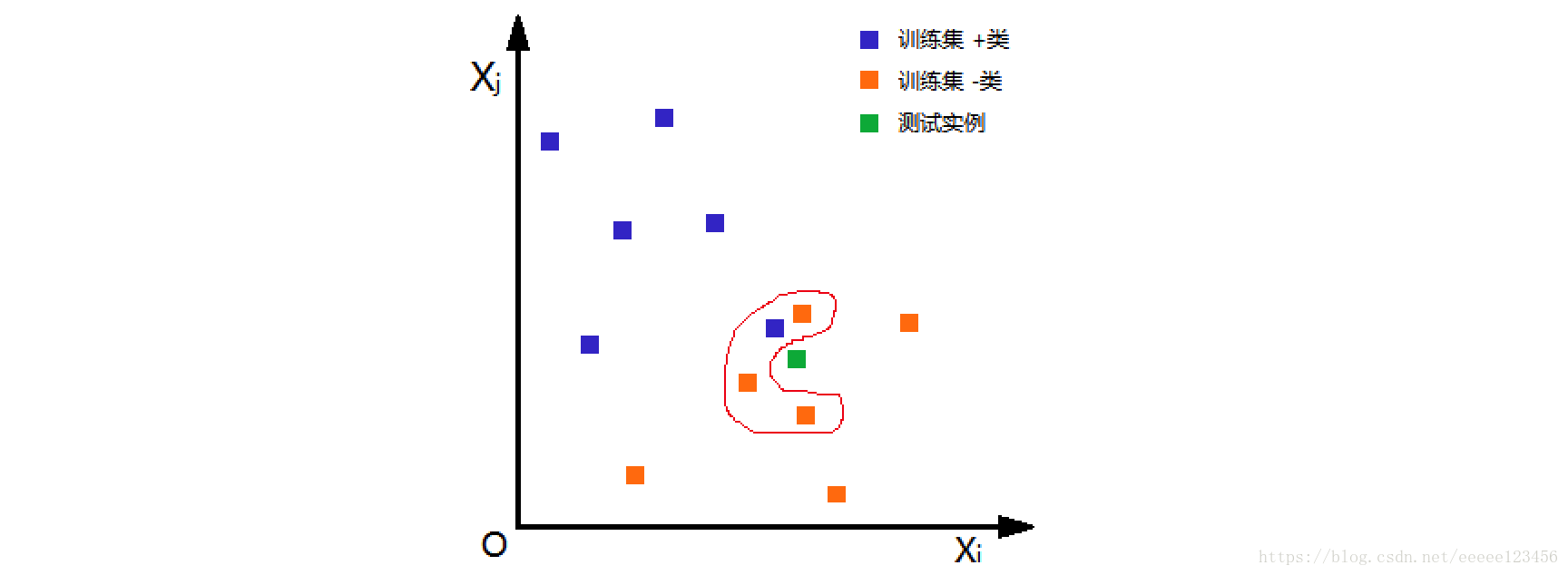
    如图1，根据欧氏距离，选择k=4个离测试实例最近的训练实例（红圈处），再根据多数表决的分类决策规则，即这4个实例多数属于“-类”，可推断测试实例为“-类”。
    k近邻法1968年由Cover和Hart提出。

图1

1.距离度量

    特征空间中的两个实例点的距离是两个实例点相似程度的反映。K近邻法的特征空间一般是n维实数向量空间Rn。使用的距离是欧氏距离，但也可以是其他距离，如更一般的Lp距离或Minkowski距离。
    设特征空间X是n维实数向量空间 $R^n$，$x_i,x_j\in X$，$x_i=(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)}{)}^T$，$x_j=(x_j^{(1)},x_j^{(2)},\cdots ,x_j^{(n)}{)}^T$，$x_i,x_j$的$L_p$ 距离定义为
$$L_p(x_i,x_j)=(\sum _{l=1}^n|{x_i}^{(l)}-{x_j}^{(l)}{|}^p{)}^{\frac{1}{p}}$$这里p≥1。
当p=1时，称为曼哈顿距离（Manhattan distance），即
$$L_1(x_i,x_j)=\sum _{l=1}^n|{x_i}^{(l)}-{x_j}^{(l)}|$$当p=2时，称为欧氏距离（Euclidean distance），即
$$L_2(x_i,x_j)=(\sum _{l=1}^n|{x_i}^{(l)}-{x_j}^{(l)}{|}^2{)}^{\frac{1}{2}}$$当p=∞时，它是各个坐标距离的最大值，即
$$L_{\infty }(x_i,x_j)=ma{x}_l|{x_i}^{(l)}-{x_j}^{(l)}|$$
证明：
以二维实数向量空间（n=2）为例说明曼哈顿距离和欧氏距离的物理意义。
① 曼哈顿距离
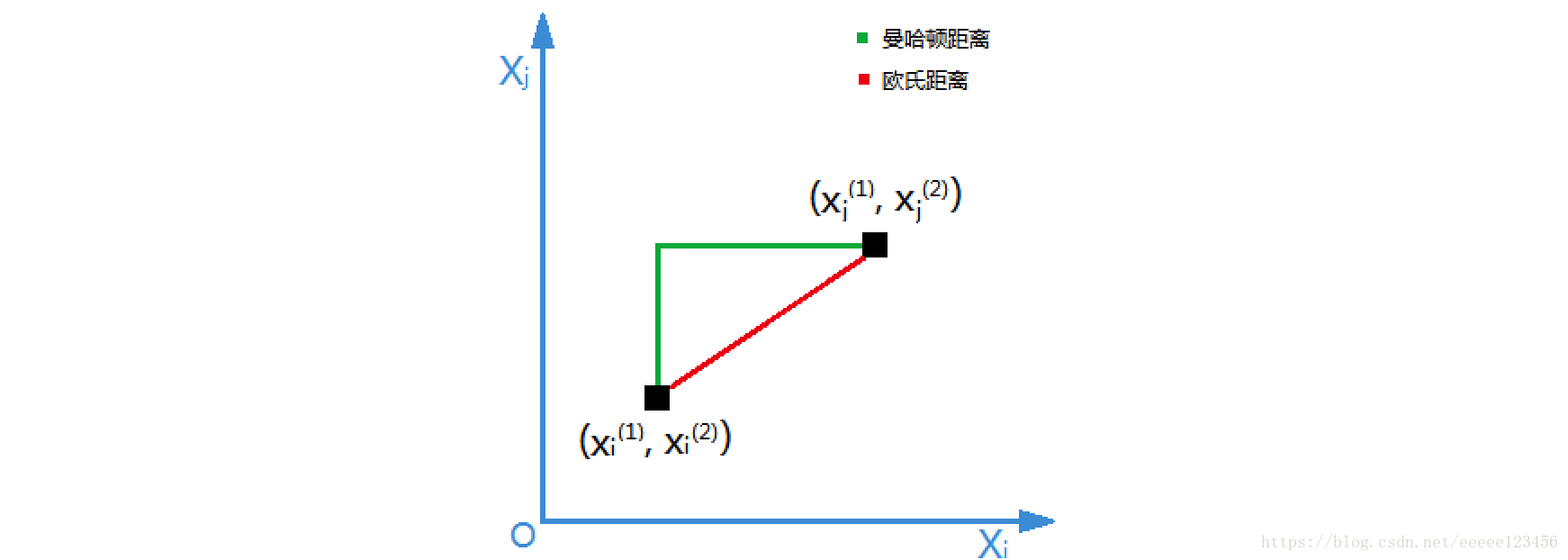
$$L_1(x_i,x_j)=\sum _{l=1}^2|{x_i}^{(l)}-{x_j}^{(l)}|=|{x_i}^{(1)}-{x_j}^{(1)}|+|{x_i}^{(2)}-{x_j}^{(2)}|$$图2绿色线即曼哈顿距离物理意义，其中横向线条表示|x₁i-x₁j|，竖向线条表示|x₂i-x₂j|。
② 欧氏距离
$$L_2(x_i,x_j)=(\sum _{l=1}^2|{x_i}^{(l)}-{x_j}^{(l)}{|}^2{)}^{\frac{1}{2}}=\sqrt[2]{|{x_i}^{(1)}-{x_j}^{(1)}{|}^2+|{x_i}^{(2)}-{x_j}^{(2)}{|}^2}$$图2红色线即欧氏距离物理意义，根据勾股定理可得。

图2

2.k值的选择

    k值的选择会对k近邻法的结果产生重大影响。在应用中，k值一般取一个比较小的数值，通常采用交叉验证法来选取最优的k值。

3.分类决策规则

    k近邻法中的分类决策规则往往是多数表决，即由输入实例的k个邻近的训练实例中的多数类，决定输入实例的类。

二、k近邻算法及代码实现（python）

1.算法

算法1（k近邻法）
输入：训练集
$$D=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$$其中，$x_i\in X\subseteq R^n$为实例的特征向量， y i ∈ Y = { c 1 , c 2 , ⋯   , c k } y_i∈Y=\{c_1,c_2,\cdots,c_k\} yi​∈Y={c1​,c2​,⋯,ck​}为实例的类别，i=1,2,…,N。
输出：实例x所属的类别y
① 根据给定的距离度量，在训练集D中找出与x最近邻的k个点，涵盖这k个点的x的领域记作$N_k(x)$
② 在$N_k(x)$中根据分类决策规则（如多数表决）决定x的类别y
$$y=argma{x}_{c_j}\sum _{x_i\in N_k(x)}I(y_j=c_j),i=1,2,\cdots ,N;j=1,2,\cdots ,K$$上式中，I为指示函数，即当y_i=c_i时I为1，否则I为0。

2.代码实现（python）

以下代码来自Peter Harrington《Machine Learing in Action》
距离度量为欧氏距离，分类决策规则为多数表决。classify0()函数有4个输入参数：用于分类的输入向量是inX，输入的训练集为dataSet，类别为labels，k表示用于选择最近邻的数目。
代码如下（保存为kNN.py）：

# -- coding: utf-8 --
from numpy import *
import operator

def createDataSet():
    # 创建训练集
    group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group, labels
	
def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    # 根据欧式距离计算训练集中每个样本到测试点的距离
    diffMat = tile(inX, (dataSetSize,1)) - dataSet
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5
    # 计算完所有点的距离后，对数据按照从小到大的次序排序
    sortedDistIndicies = distances.argsort()
    # 确定前k个距离最小的元素所在的主要分类，最后返回发生频率最高的元素类别
    classCount={}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

运行命令如下：

group和labels为训练集，其中group为特征向量，labels为类别。输入测试实例[0,0]，选取与测试实例距离最近的3个元素，最后返回这3个元素中发生频率最高的元素类别，即为kNN近邻法的预测值。

三、k近邻法的实现：kd树

    实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索，这点在特征空间的维数大及训练数据容量大时尤其必要。
    k近邻法最简单的实现方法是线性扫描（linear scan），这时要计算输入实例与每一个训练实例的距离，当训练集很大时，计算非常耗时。为了提高k近邻法搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。具体方法很多，下面介绍其中的kd树方法（kd树是存储k维空间数据的树结构，这里的k与k近邻法的k意义不同）。

1.构造kd树

    kd树是二叉树，是一种对k维空间中实例点进行存储以便对其进行快速检索的树形数据结构。kd树表示对k维空间的一个划分（partition），构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。
    通常，依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的中位数（一组数据按大小顺序排列起来，处于中间的一个数或最中间两个数的平均值。本文在最中间有两个数时选择最大值作中位数）为切分点，这样得到的kd树是平衡的。注意，平衡的kd树搜索时未必是最优的。

2.算法

算法2（构造平衡kd树）
输入：k维空间数据集
D = { x 1 , x 2 , ⋯   , x n } D=\{x_1,x_2,\cdots,x_n\} D={x1​,x2​,⋯,xn​}其中$x_i=(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)}{)}^T，i=1,2,\cdots ,N$
输出：kd树
① 开始：构造根结点，根结点对应于包含D的k维空间的超矩形区域。
   选择x₁为坐标轴，以D中所有实例的x₁坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x₁垂直的超平面实现。
   由根结点生成深度为1的左、右子结点：左子结点对应坐标x₁小于切分点的子区域，右子结点对应坐标x₁大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。
② 重复：对深度为j的结点，选择xl为切分的坐标轴，l=j(mod k)+1，以该结点的区域中所有实例点的xl坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴xl垂直的超平面实现。
   由该结点生成深度为j+1的左、右子结点：左子结点对应坐标xl小于切分点的子区域，右子结点对应坐标xl大于切分点的子区域。将落在切分超平面上的实例点保存在该结点。
③ 直到两个子区域没有实例存在时停止，从而形成kd树的区域划分。
例1 给定一个二维空间的数据集：$$D=\{(2,3{)}^T,(5,4{)}^T,(9,6{)}^T,(4,7{)}^T,(8,1{)}^T,(7,2{)}^T\}$$构造一个平衡kd树。
解：D为二维空间，则k=2。
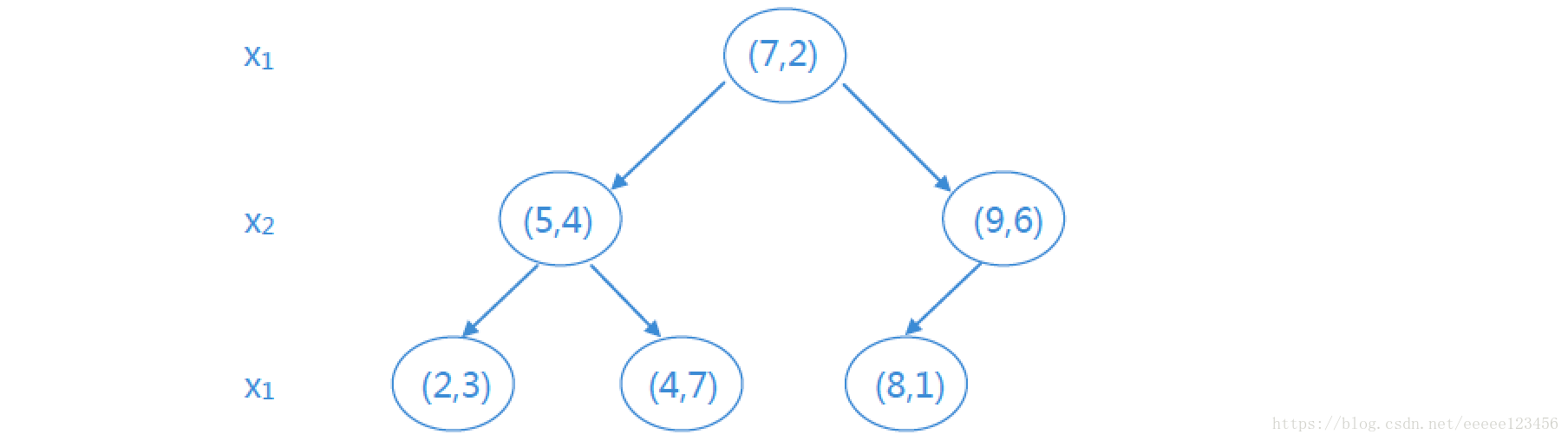
① D中6个实例的x₁坐标的中位数为7，则以(7 , 2)为切分点，由通过切分点并与坐标轴x₁垂直的平面将超矩形区域切分为两个子区域。根结点为(7 , 2)，左区域包括：(2 , 3) , (5 , 4) , (4 , 7)，右区域包括：(8 , 1) , (9 , 6)，深度为1
② 对深度为j=1的结点，选择l=j(mod k)+1=1(mod 2)+1=2即x₂为切分的坐标轴。则左区域的切分点为(5 , 4) ，左子区域为(2 , 3)，右子区域为(4 , 7)；右区域的切分点为(9 , 6) ，左子区域为(8 , 1)。
如此递归，最后得到的平衡kd树如下所示：

3.搜索kd树（未完，待续）

以上全部内容参考书籍如下：
李航《统计学习方法》
周志华《机器学习》
Peter Harrington《Machine Learing in Action》