地球上两点间最短距离及计算方法
一、为什么说“地球表面两地之间的最短距离是通过这两点的大圆的劣弧段”?
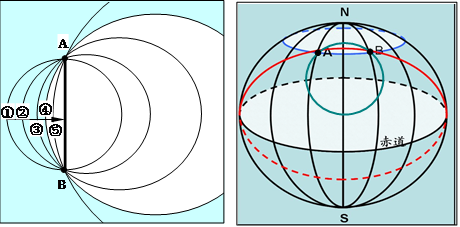
如上左图所示:AB两点间最短距离是线段AB,即图中较粗的黑线。从其他的①—⑤弧线可以看出二个特点:一是都长于线段AB,二是从①到⑤逐步变短。因此我们可以想象当通过A、B点的弧线半径无穷大时,其上的弧AB接近线段AB,所以有“球面两地之间的最短距离是通过这两点的大圆的劣弧段”。该定理同样适用于立体几何,如右图所示。
二、地球表面两点间最短距离
1、常见的地球队上的大圆有三个(类):赤道、经线圈、晨昏线。
2、如果两点的经度相差不大(在3°以内),可近似看作在同一经线上,最短距离=纬差×111KM;如果两点的纬度相差不大(在3°以内),可近似看作在同一纬线上,最短距离=经差×COS纬度×111KM。
三、地球上两点间最短距离的走法
1、若两点在赤道上,则两点间最短航线应是沿着赤道朝两点间的劣弧方向运动,即向东或向西。
2、若两点在同一条经线上,则两点间最短航线应是沿着经线朝两点间的劣弧方向运动,即向北或向南。
3、若两地的经度差等于180,则经过这两点大圆是经线圈。这两点间的最短距离是经过极点。
①同在北半球,最短航线必须经过北极点,其航行方向一定是先向正北,过北极点后再向正南。
②同在南半球,最短航线必须经过南极点,其航行方向一定是先向正南,过南极点后再向正北。
③两地位于不同半球,这时需要考虑经过北极点为劣弧,还是经过南极点为劣弧,然后确定最短航线的走向和航程。
4、若两地的经度差不等于180,则经过这两点大圆不是经线圈,而是与经线圈斜交,其最短航线不经过极点,具体分为两种情况:
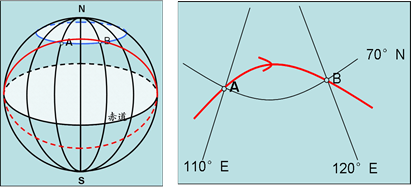
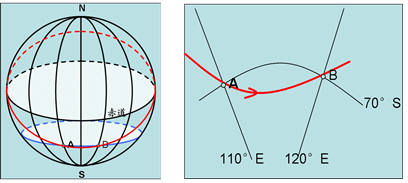
①甲地位于乙地的东方,从甲到乙最短航程为:同在北半球,先向西北,再向西,最后向西南;同在南半球,先向西南,再向西,最后向西北;位于不同半球时,需要讨论哪一段为劣弧段。
② 甲地位于乙地的西方,从甲到乙最短航程为:同在北半球,先向东北,再向东,最后向东南;同在南半球,先向东南,再向东,最后向东北;位于不同半球时,需要讨论哪一段为劣弧段。
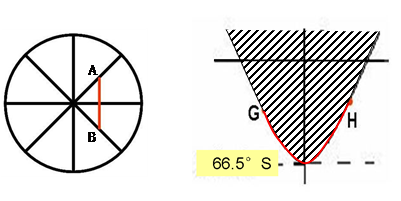
5、俯视图,经过两点的大圆的劣弧部分形状可视为两点间的直线(如图)。
6、晨昏线上两点之间的最短距离即该晨昏线上两点之间的劣弧部分。(如下图中的GH之间)
在计算任意两点之前的距离时,有如下两种方法:一种利用勾股定理计算,适用于两点距离很近的情况;一种按标准的球面大圆劣弧长度计算,适用于距离较远的情况。
static double DEF_PI = 3.14159265359; // PI
static double DEF_2PI= 6.28318530712; // 2*PI
static double DEF_PI180= 0.01745329252; // PI/180.0
static double DEF_R =6370693.5; // radius of earth
public double GetShortDistance(double lon1, double lat1, double lon2, double lat2)
{
double ew1, ns1, ew2, ns2;
double dx, dy, dew;
double distance;
// 角度转换为弧度
ew1 = lon1 * DEF_PI180;
ns1 = lat1 * DEF_PI180;
ew2 = lon2 * DEF_PI180;
ns2 = lat2 * DEF_PI180;
// 经度差
dew = ew1 - ew2;
// 若跨东经和西经180 度,进行调整
if (dew > DEF_PI)
dew = DEF_2PI - dew;
else if (dew < -DEF_PI)
dew = DEF_2PI + dew;
dx = DEF_R * Math.cos(ns1) * dew; // 东西方向长度(在纬度圈上的投影长度)
dy = DEF_R * (ns1 - ns2); // 南北方向长度(在经度圈上的投影长度)
// 勾股定理求斜边长
distance = Math.sqrt(dx * dx + dy * dy);
return distance;
}
public double GetLongDistance(double lon1, double lat1, double lon2, double lat2)
{
double ew1, ns1, ew2, ns2;
double distance;
// 角度转换为弧度
ew1 = lon1 * DEF_PI180;
ns1 = lat1 * DEF_PI180;
ew2 = lon2 * DEF_PI180;
ns2 = lat2 * DEF_PI180;
// 求大圆劣弧与球心所夹的角(弧度)
distance = Math.sin(ns1) * Math.sin(ns2) + Math.cos(ns1) * Math.cos(ns2) * Math.cos(ew1 - ew2);
// 调整到[-1..1]范围内,避免溢出
if (distance > 1.0)
distance = 1.0;
else if (distance < -1.0)
distance = -1.0;
// 求大圆劣弧长度
distance = DEF_R * Math.acos(distance);
return distance;
}
double mLat1 = 39.90923; // point1纬度
double mLon1 = 116.357428; // point1经度
double mLat2 = 39.90923;// point2纬度
double mLon2 = 116.397428;// point2经度
double distance = GetShortDistance(mLon1, mLat1, mLon2, mLat2);








 本文介绍了地球表面上两点间最短距离的计算方法及其走法。包括如何利用大圆的劣弧段确定最短路径,并提供了针对不同位置关系的具体航行指导。此外,还给出了两种计算距离的公式,分别适用于近距离和远距离的情况。
本文介绍了地球表面上两点间最短距离的计算方法及其走法。包括如何利用大圆的劣弧段确定最短路径,并提供了针对不同位置关系的具体航行指导。此外,还给出了两种计算距离的公式,分别适用于近距离和远距离的情况。
















 1169
1169

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








