两圆相交求面积

两圆相交求面积，考虑两圆的位置关系再计算其面积：

（因为是计算面积，不考虑两圆相切的情况）

1.两圆相离：

判定条件：两圆半径之和大于等于圆心距

计算方法：显然相交面积为0

2.两圆相含：两圆半径之差小于等于圆心距

计算方法：显然相交面积为较小圆的面积

3.两圆相交：以上两种情况以外

计算方法：

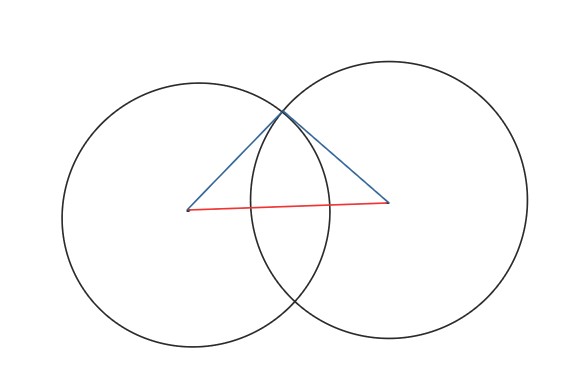
用余弦定理得三角形圆心处的角度，然后计算两个扇形的面积，再减去三角形的面积，虽然中间部分被计算了两次，但是因为相交部分以圆心连线分成对称两块，所以正好得到的就是两圆相交面积。

两圆相交求面积模板：

#include <cstdio>
#include <cmath>

struct Circle {
    double x, y, r;
};

double calarea(Circle c1, Circle c2) {
    double dis = sqrt((c1.x - c2.x) * (c1.x - c2.x) + (c1.y - c2.y) * (c1.y - c2.y));
    if(c1.r + c2.r <= dis) return 0;//两圆相离
    if(c1.r - c2.r >= dis)//两园相含 c1包含c2
        return acos(-1.0) * c2.r * c2.r;
    if(c2.r - c1.r >= dis)//两园相含 c2包含c1
        return acos(-1.0) * c1.r * c1.r;
    //两圆相交
    double angle1 = acos((c1.r * c1.r + dis * dis - c2.r * c2.r) / (2 * dis * c1.r));
    double angle2 = acos((c2.r * c2.r + dis * dis - c1.r * c1.r) / (2 * dis * c2.r));
    return c1.r * c1.r * angle1 + c2.r * c2.r * angle2 - sin(angle1) * c1.r * dis;
}

典型题目：

hdu 5120

题意：计算两个相同圆环的相交面积。

思路：先计算两个大圆的相交面积，再减去两倍的小圆和大圆相交的面积，再加上两个小圆相交的面积。

AC代码：

#include <cstdio>
#include <cmath>

struct Circle {
    double x, y, r;
};

double calarea(Circle c1, Circle c2) {
    double dis = sqrt((c1.x - c2.x) * (c1.x - c2.x) + (c1.y - c2.y) * (c1.y - c2.y));
    if(c1.r + c2.r <= dis) return 0;//两圆相离
    if(c1.r - c2.r >= dis)//两园相含 c1包含c2
        return acos(-1.0) * c2.r * c2.r;
    if(c2.r - c1.r >= dis)//两园相含 c2包含c1
        return acos(-1.0) * c1.r * c1.r;
    //两圆相交
    double angle1 = acos((c1.r * c1.r + dis * dis - c2.r * c2.r) / (2 * dis * c1.r));
    double angle2 = acos((c2.r * c2.r + dis * dis - c1.r * c1.r) / (2 * dis * c2.r));
    return c1.r * c1.r * angle1 + c2.r * c2.r * angle2 - sin(angle1) * c1.r * dis;
}

main() {
    Circle c1, c2;
    int t;
    scanf("%d", &t);
    for(int tcase = 1; tcase <= t; tcase++) {
        double r, R;
        scanf("%lf %lf", &r, &R);
        scanf("%lf %lf", &c1.x, &c1.y);
        scanf("%lf %lf", &c2.x, &c2.y);
        double ans = 0;
        c1.r = c2.r = R;
        ans += calarea(c1, c2);
        c1.r = R,  c2.r = r;
        ans -= 2 * calarea(c1, c2);
        c1.r = c2.r = r;
        ans += calarea(c1, c2);
        printf("Case #%d: %.6f\n", tcase, ans);
    }
}