2022新高考I卷 数学 题解

——你写这个的意义是？
——留下一点深刻的印象，顺便上个号发扬一下OI传统。

复盘

太长不看：因为各种解析几何和三角函数不熟悉全程被工地折磨。

自行掐表2个小时。
首先T1上来就被阴了，险些 $\sqrt{x}<4\Rightarrow x<2$ ，感觉不妙。
于是就开始拉胯，T4棱台公式忘了去查了一下，可以算-5，到T8的时候非常naive的认为就是过半径的时候体积最小于是选错了，-5.
填空题倒是没有出错，唯一的问题大概是T16做的时间太长了。
T17一个常规累乘。
T18对于我这个三角函数非常拉的就有点折磨，(2)先是试图余弦定理被折磨，然后推了一顿等量关系又被折磨，熟练度实在是太低了。
T19差点卡(1)，好在反应过来了，不难。
T20非常亲民，做过的题而且数挺好算的（这题网上答案还有些给的不对，去跟99.9%比了）。
T21又是被疯狂折磨，(1)化简了一万年，严重影响节奏，而且更大的问题在于这地方我当成椭圆做了半天，只剩不到15分钟，直接弃了(2)。
T22(1)算是一个不太容易解决的(1)，(2)倒是真的不难，讨论单调性画个图直接一个不能更明显的同构直接解决。这题网上的答案花了非常大的功夫讨论 $y=b$ 与两个函数的交点情况，我实在有点不能理解，不过仔细看了一下发现其实证明的东西就是分别说一下单调性画在一个图上的过程，他甚至没有讨论渐近线，说的比我还不严谨，那就姑且当作没什么问题了。
对答案，除了T8 T21(2)之外结果算的是对的，过程也没有太多别扭的地方。考虑到棱台公式是查的，严谨起见算个132左右的分数吧。

部分题解

题解完全主观，不涉及严谨的评分标准的讨论，仅包括我本人的体会和解。

T4套棱台公式即可。鉴于我忘了，补一下这个公式：
$$V=\frac{1}{3}h(S1+S2+\sqrt{S1S2})$$
T6我做的时候往里面代入 $\frac{3}{2}\pi wx+\frac{\pi }{4}=2k\pi$ ，实在是人类迷惑行为，显然应该化成 $w=\frac{8k-1}{6}$ 再求。

T7是一个比较麻烦的题，显然不能用同一个函数同构，只能分别去比。
$ac$ $bc$ 相对容易比较， $ab$ 这一组需要移项后同取倒数变成 $e^{-\frac{1}{10}}$ 比较 $1-\frac{1}{10}$ ，这地方得注意在指数对数和一般情况下取倒数和取相反数的互相转化不能混了 （比如我就混了）

T8，设高和侧棱的夹角为 $\theta$ ，高为 $l\cos \theta$ ，底面对角线长为 $2l\sin \theta$ ,通过余弦定理和半径结合可以算出来 $\cos \theta =\frac{l}{6}$ ，这个三棱锥的体积 $V=\frac{1}{3}l\cos \theta \times (2l\sin \theta {)}^2\times \frac{1}{2}=\frac{2}{3}{l}^3\cos \theta {\sin }^2\theta =144(\sin \theta {\cos }^2\theta {)}^2=144(\sin \theta -{\sin }^3\theta {)}^2$ ，而 $\sin \theta \in [\frac{1}{2},\frac{\sqrt{3}}{2}]$ 且单调变化，所以可以直接对 $V$ 求导（可以换个元看着顺眼一点），发现极小值点是 $\frac{\sqrt{3}}{3}$ ，最终 $V\in [\frac{64}{3},\frac{27}{4}]$ ，选择C.
这道题其实推导的过程并不难想，主要是不能太想当然。

T11小工地，直接按要求搬砖即可。注意别把 $|OP|\cdot |OQ|$ 和 $OP\cdot OQ$ 混了。

T12是一个比较新鲜的题， $f(x)$ 关于 $x=\frac{3}{2}$ 对称而 $f^{\prime }(x)$ 关于 $x=2$ 对称。前者说明 $f^{\prime }(x)$ 关于 $(\frac{3}{2},0)$ 对称，后者说明 $f(x)$ 关于 $(2,t)$ 对称，四个选项代入试一下就行了。这个互相对称还是很有意思的。这道题不建议去思考图象是什么样的，毕竟选项中没有研究过函数整体，纯粹多此一举。

T16看到周长基本就确定这题应该就是在求 $a$ ，小工地。这个题的图不太容易画，很容易就糊成一团了，况且有等边三角形的性质之后根本也不需要图了，所以画个图能看出来是 $4a$ 就够了，我这图反反复复的画属实是浪费时间。

T18(2)在 $\sin \cos$ 中间一顿推就行了，一般人应该不会像我一样在这种愚蠢的地方卡两三分钟。由于这个题的性质主要出在角度上，所以用余弦定理不太合理，我这里是因为沿用了上一问的条件，于是想到了余弦定理。属于是非常低级的失误。

T19(1)不要直接默认 $BC\perp A_{1}B$ ，要不是(2)我就假证了。用体积互相转化一下就行了，并不难。

T21卡我卡的就比较严重了。
首先(1)就是一个不算很小的工地，经过一顿推能得出 $2k^2+(b+1)k+b-1=0$ ，也没有什么别的路了，显然就是得对着这个式子配。
这个东西愣配并不好配，一种比较好的方法是，由于直线过 $A$ 的时候显然斜率和为0，此时 $2k+b-1=0$ ，那么这个多项式就应该配成一个 $(mk+n)(2k+b-1)$ 的格式，代入一下就能得出 $k=-1$ ，避免了大量无用的尝试时间（这地方我是强行试出来的，要不是这个配花了我大量的时间可能我就尝试一下(2)了）

(2)上来先尝试了一下 $\cos \theta =\frac{1}{3}$ 然后结合向量算，非常难搞。这个题的关键性质是斜率和为0，所以这个倾角可以直接求出来。

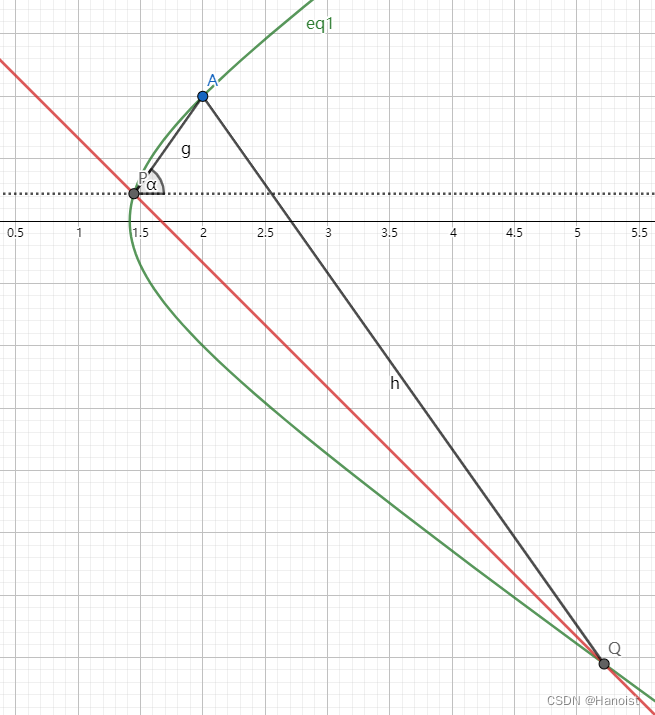
包含 $\alpha$ 的这个三角形是一个等腰三角形，可以直接求出来 $\tan \alpha =\sqrt{2}$ ，有了这个可以直接把上面的 $b$ 也求出来，这个时候再去用韦达定理倒就行了。

T22的(1)直接分别求一下单调性然后合在一起得到 $a-alna=1+lna$ ，再求导就行了。(2)直接顺着(1)先把单调性和图象形态直接推完。

可以发现有三个交点的情况只有一个，这个是显然的。吃饱了撑的严谨起见可以再对这两个函数的差求个导研究一下，会发现这个差值函数也是单调的，所以交点只可能有一个。
交点从左到右设为 $x_1{x}_2{x}_3$ ，有 $e^{x_2}+ln{x}_2=2x_2$ ，又因为 $f(x_1)=f(x_2)=g(x_2)=g(x_3)$ ，由于这两个函数可以同构，讨论一下取值范围（同构的时候特别得注意自变量取值范围）就可得 $x1=lnx2,x2=lnx3$ ，代入一下就结束了。

所以总体上来说这套卷子的主要难点在于工地确实比较多，确实容易做起来卡手（当然这个主要是我自己不熟练导致的）。

全国II卷晚上做一下，到时候再看看它们的共通之处。