前言
最短路问题(shortest path problem, SSP)是图论的经典问题之一,基本内容是:在一个由边和点组成的有向图(or无向图)中,基于每一条边的属性(比如长度、成本、时间等),寻找两点之间总权最小的路径问题。
最短路问题的求解方法有很多,比如Dijkstra算法、Ford算法等,本文主要介绍整数规划解法。
1. 案例介绍
图1是一个由边和点组成的有向图,其中每一条边都有相应的权重,求从起点A到终点G的最短路径
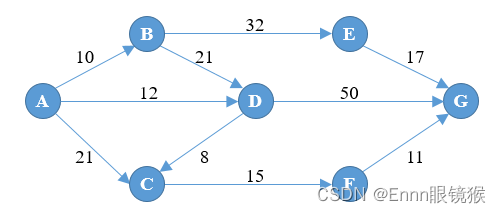
2. 整数规划模型构建
2.1. 梳理模型思路
如图1所示,从A到G的任意一条路径如下,左图是有向图中该路径涉及的点与线,右图是剩余的点与线,先定义两个概念:
- 点入集:进入该点的线的集合
- 点出集:离开该点的线的集合
可发现以下几点:
- 选择某条路径时,起点的点出集中被选择的线数量-点入集的 = 1
- 选择某条路径时,终点的点出集中被选择的线数量-点入集的 = -1
- 选择某条路径时,其余点的点出集中被选择的线数量-点入集的 = 0
- 未选择的点,其余点的点出集中被选择的线数量-点入集的 = 0
因此,可以根据以上四点特点,建立线性优化模型和约束函数
 | 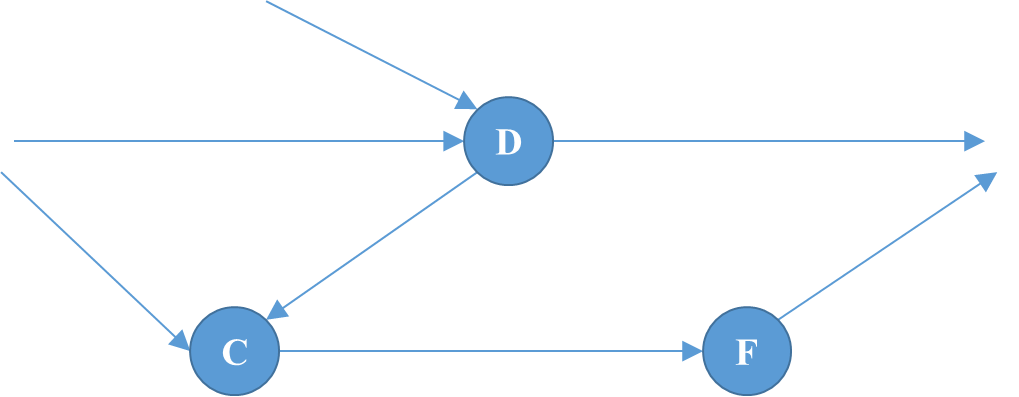 |
| 该路径涉及的点与线 | 某路径未涉及的点与线 |
2.2. 构建自变量
设二元变量,表示点
到点
的线条
是否被最优路径选中
![]()
2.3. 构建目标函数
基于路径中所有线条的加权和最小构建整数规划的目标函数
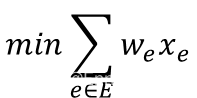
式中,表示线条权重,
表示所有线条
的集合
2.4. 构建约束条件
设点的点出集为
,点
的点入集为
,且
;为所有点整理出
,针对各个点建立约束条件:
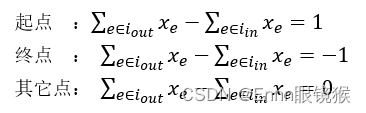
3. 基于Python+Pulp求解实现
3.1. 构建有向图处理类
class CaseData:
def __init__(self, edgeMap):
# key-边编号,value-边权重
self.edgeMap = edgeMap
# 边编号集合
self.edges = list(self.edgeMap.keys())
# 点编号集合
self.plots = self._getPlots()
# 起点与终点(也可随意选一点)
self.startPlot = self._getStartSpot()
self.endPlot = self._getEndSpot()
# key-plot,value-{"out": 边的列表,"in": 边的列表}
self.plotMap = self._getPlotMap()
def _getPlotMap(self):
plotMap = {}
for plot in self.plots:
if plot not in plotMap.keys():
plotMap[plot] = {"out": [], "in": []}
for edge in self.edges:
if plot == edge[0]:
plotMap[plot]["out"].append(edge)
elif plot == edge[-1]:
plotMap[plot]["in"].append(edge)
return plotMap
def _getPlots(self):
plots = set()
for edge in self.edges:
for plot in list(edge):
plots.add(plot)
return list(plots)
def _getStartSpot(self):
startPlots = copy.copy(self.plots)
for edge in self.edges:
if edge[-1] in startPlots:
startPlots.remove(edge[-1])
return startPlots[0]
def _getEndSpot(self):
startPlots = copy.copy(self.plots)
for edge in self.edges:
if edge[0] in startPlots:
startPlots.remove(edge[0])
return startPlots[0]
3.2. 建立整数规划模型
class SppProgram:
def __init__(self, problemType=None):
self.setProblemType = "min" if problemType is None else problemType
self.lpStatus = None
self.varValuesMap = {}
self.objectValue = None
def setSppModel(self, caseData):
# 1. 建立问题
prob = LpProblem("最短路问题", LpMinimize) if self.setProblemType == "min" else LpProblem("最短路问题", LpMaximize)
# 2. 建立变量(以列表形式建立多个变量,变量名为边名)
edges = caseData.edges
vars = LpVariable.dicts("x", edges, cat="Binary")
# 3. 目标函数
prob += lpSum(caseData.edgeMap[_] * vars[_] for _ in caseData.edges), "路径总权重"
# 4. 约束条件
for plot in caseData.plots:
if plot == caseData.startPlot:
prob += lpSum(vars[_] for _ in caseData.plotMap[plot]["out"]) - \
lpSum(vars[_] for _ in caseData.plotMap[plot]["in"]) == 1, "起点"
elif plot == caseData.endPlot:
prob += lpSum(vars[_] for _ in caseData.plotMap[plot]["out"]) -\
lpSum(vars[_] for _ in caseData.plotMap[plot]["in"]) == -1, "终点"
else:
prob += lpSum(vars[_] for _ in caseData.plotMap[plot]["out"]) -\
lpSum(vars[_] for _ in caseData.plotMap[plot]["in"]) == 0
# 5. 求解
prob.solve()
# 6. 保存求解状态
self.lpStatus = LpStatus[prob.status]
# 7. 保存每个变量的最优值
for varName in prob.variables():
self.varValuesMap[varName] = varName.varValue
# 8. 保存最优解的目标函数值
self.objectValue = value(prob.objective)
3.3. 带入案例中的有向图数据
if __name__ == "__main__":
edgeMap = {"AB": 10, "AC": 21, "AD": 12,
"BD": 21, "BE": 32,
"CF": 15,
"DC": 8, "DG": 50,
"EG": 17,
"FG": 11}
caseData = CaseData(edgeMap=edgeMap)
lpModel = SppProgram("min")
lpModel.setSppModel(caseData=caseData)
# 输出最优解路径集
varValuesMap = lpModel.varValuesMap
print([_ for _ in varValuesMap.keys() if varValuesMap[_] == 1])
3.4. 查看最优路径

即最优路径为:AD→DC→CF→FG
注意:当存在多个最优解时,Pulp无法返回所有最优解,只会选择其中之一为最优解
案例与代码文件下载链接:![]() https://download.csdn.net/download/ennnnnnnnnnnnnnn/87441544
https://download.csdn.net/download/ennnnnnnnnnnnnnn/87441544






















 5550
5550











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








